Физика/7. Оптика
Сашкова Я. В., Одаренко Е. Н.
Харьковский национальный университет радиоэлектроники,
Украина
ИССЛЕДОВАНИЕ
ФОКУСИРУЮЩИХ СВОЙСТВ
ЦИЛИНДРИЧЕСКИХ МНОГОСЛОЙНЫХ
ЛИНЗ
Задачи, связанные с рассеянием
электромагнитного излучения на цилиндрических структурах, довольно давно
привлекают внимание исследователей. Причиной этого является базовый характер
таких объектов для различных отраслей радиоэлектроники и оптики. Дифракция волн
на цилиндрах различных конфигураций интенсивно исследуется в различных отраслях
науки и техники [1, 2].
В частности, многослойные
цилиндры используются для моделирования оптических волокон и различных
устройств градиентной оптики, среди которых наиболее известными являются линзы
Лунеберга и Итона-Липмана [3].
Перспективным также
является изучение одной из классических разновидностей градиентных оптических
систем – линзы под названием «рыбий глаз» Максвелла [4]. В этой системе
отсутствуют все аберрации, кроме дисторсии и кривизны поля изображения.
В данной работе рассматривается важная
проблема визуализации двумерного пространственного распределения
электромагнитного поля волны, рассеянной на многослойном диэлектрическом
цилиндре. С помощью разработанного расчетного проекта (использовалась система
компьютерной алгебры MathCAD)
получены пространственные распределения амплитуды электрического поля внутри и
за пределами многослойной линзы. Проект позволяет
проводить исследования для произвольного количества слоев структуры, их
геометрических размеров и материальных параметров. Следует отметить, что
показатели преломления слоев могут быть отрицательными, т.е. разработаны
средства компьютерного моделирования для исследования структур, содержащих
метаматериалы.
Рассматривается бесконечный вдоль оси Oz многослойный цилиндр (количество слоев 
) с произвольными материальными параметрами. Показатель
преломления сердцевины 
, показатель преломления слоев 
, где 
– номер слоя. Вдоль положительного
направления оси Оx на структуру падает
электромагнитная волна с параллельной поляризацией. Это означает, что вектор
напряженности электрического поля направлен параллельно образующей цилиндра,
т.е. вдоль оси Oz. Схема исследуемой структуры представлена
на рис. 1.
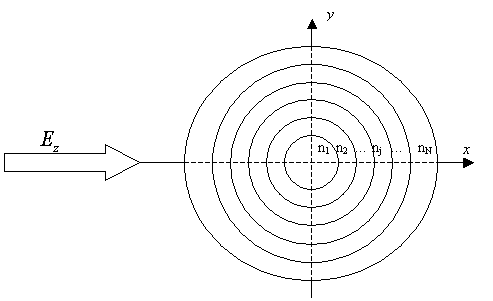
Рисунок 1 – Падение волны на многослойный цилиндр
Для записи полей в
различных областях исследуемой системы используется стандартное представление
через цилиндрические функции:
· Волна, падающая на цилиндр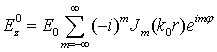 
(1)
· Рассеянная цилиндром волна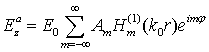 
(2)
· Поле в сердцевине структуры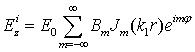 
(3)
·
Поле внутри j-го
слоя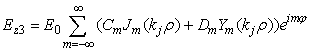 
(4)
Здесь: 
– функция Бесселя; 
– функция Неймана; 
– функция Ханкеля
1-го рода; 
, 
, 
– волновые числа
окружающей среды, сердцевины цилиндра и 
-го слоя соответственно; 
, 
, 
, 
– амплитудные
коэффициенты.
Решение такой задачи даже
для небольшого количества слоев является весьма громоздким и приводит к сложным
выражениям для неизвестных амплитудных коэффициентов. Поэтому при реализации
расчетного алгоритма была выбрана
матричная форма записи системы линейных алгебраических уравнений:
, (5)
где 
– матрица системы; 
– вектор-столбец
неизвестных коэффициентов; 
– вектор-столбец
правых частей неоднородной системы уравнений.
В этом случае для решения
системы уравнений можно использовать хорошо развитый аппарат компьютерных матричных
вычислений и в итоге свести расчеты к простой операции перемножения двух матриц:
. (6)
На рис.
2 представлены результаты расчета пространственного распределения интенсивности
электрического поля, рассеянного многослойным цилиндром. Количество слоев N =
10, отношение диаметра цилиндра к длине падающей волны D/λ = 0,1
(рис. 2а) и 0,2 (рис. 2б). Толщина слоев на рис. 2а увеличивается в
арифметической прогрессии с шагом d=0.15,
на рис 2б изменяется периодически: 0,1 и 0,2 мм. Показатель преломления линейно
возрастает от центра к периферии.
Очевидно,
что в данном случае происходит фокусировка излучения внутри многослойной
структуры. На рис. 2а наблюдается формирование одного фокуса в пределах
многослойной оболочки. В системе с периодической струк-
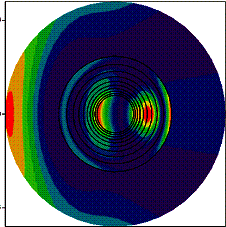
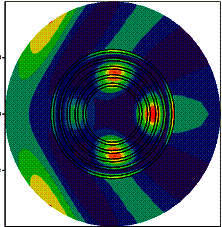
(а) (б)
Рисунок
2 – Результаты расчета
турой оболочки очевидно наличие четырех фокусов,
равномерно распределенных по азимутальной координате (рис. 2б). Следовательно,
в этом случае фактически происходит формирование кольцевого резонатора.
Наглядное представление
пространственного распределения рассеянного поля позволяет исследовать фокусирующие
свойства различных градиентных систем с цилиндрической симметрией.
Список источников
1. Muhammad A.
Analytical solution to scattering of N plane waves by a coated circular
cylinder // Int.
Conf. on Electromagnetics, Wireless
and Optical Communications. – 2005. – P. 130-136.
2. Hongo
K., Kumazawa M., Hori H. Scattering of electromagnetic plane waves by a
circular cylinder // IEEE Transactions. – 1977. – Vol. 25. – P. 898 –
900.
3.
Котляр В.В.,
Личманов М.А. Дифракция плоской электромагнитной волны на градиентном
диэлектрическом цилиндре // Компьютерная оптика. – 2003. – Вып.
25 – С. 11–15.
4. Kinsler P., Tan J., Thio T., Trant C., Kandapper N. Maxwell's Fishpond // Eur. J. Phys. – 2012. – Vol.33. – P.
1737-1750.