Технічні науки / 2. Механіка

К.ф.-м.н., доцент Сяський В.О.

Національний університет водного господарства та природокористування

Визначення напруженого стану складених пластин з розімкнутим круговим ребром жорсткості

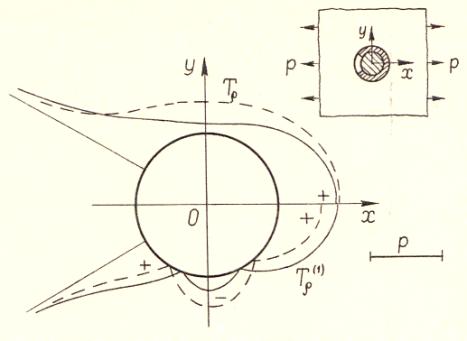
Розглянемо кусково-однорідну ізотропну пластинку, що складається із нескінченної пластинки товщиною 2h з круговим отвором радіусом ρ₀=1 і кругової пластинки (диска), які на ділянці L₁=[-α₀, α₀] (α₀<π) спаяні між собою за допомогою частини тонкого пружного кільця (стрижня) сталого поперечного перерізу 2h₀×b₀, що володіє жорсткостями на розтяг А (λ) і згин В (λ) у своїй площині. Дана система знаходиться під дією взаємно перпендикулярних розтягувальних зусиль інтенсивностей p і q, прикладених на нескінченності; зовнішнє навантаження на лінії спаю і вільних берегах L₂, які в процесі деформації не контактують, відсутнє.

Кільце вважаємо пружною лінією, що лежить в серединній площині пластинок, яку ототожнюємо з контуром L₁, тому деформації пластинок на лінії спаю будуть однаковими. Потрібно визначити напружений стан в пластинках на лінії розмежування матеріалів.

Припустимо, що спільна серединна площина кусково-однорідної пластинки віднесена до полярної системи координат (ρ, λ) з полюсом в центрі диска, а полярна вісь співпадає з віссю Ох і проходить через середину стрижня, утворюючи з напрямом дії зусилля р кут β₀ (рис. 1).

Умовно відокремимо стрижень від пластинок, замінивши його дію невідомими нормальними і дотичними зусиллями. Тут і далі величини з індексом „1” відносяться до диска і мають той же фізичний зміст, що і величини без індексів для нескінченної пластинки з отвором.

Напружений стан на контурі кругового отвору в нескінченній пластинці визначається величинами U і V, які мають вигляд 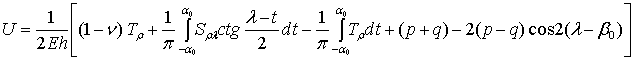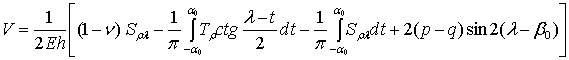[1]:

,

. (1)

де Е, ν – модуль пружності і коефіцієнт Пуассона матеріалу пластинки.

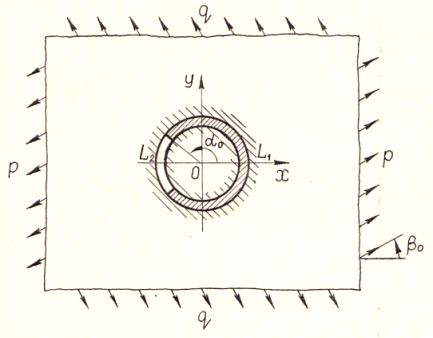
Рис. 1. Кусково-однорідна пластинка

з розімкнутим круговим ребром жорсткості

Аналогічно знаходяться величини U₁ і V₁ для кругової пластинки:

,

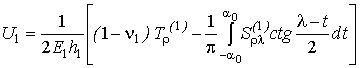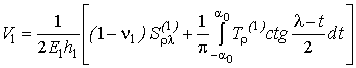. (2)

Граничні умови спаю пластинок і стрижня мають вигляд:

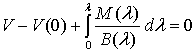, , , (3)

де Р(λ) і М(λ) – поздовжня сила і згинний момент у перерізі λ стрижня, причому

,

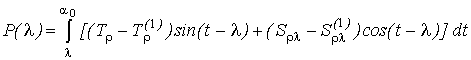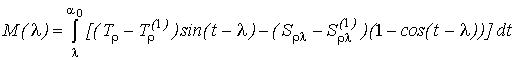. (4)

На вільних берегах пластинок

. (5)

Співвідношення (1) – (4) призводять до системи чотирьох сингулярних інтегральних рівнянь відносно контактних зусиль T_ρ, S_ρλ, , яка в комплексній формі представлена таким чином:

,

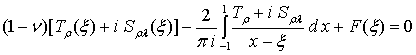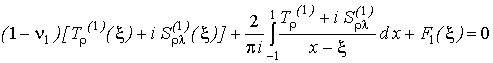(6)

Тут F(ξ), F₁(ξ) – неперервні по ξ на відрізку [-1, 1] функції, що задовольняють умові Гельдера.

За допомогою методики [2] доведено, що розв’язок системи (6) необхідно шукати у вигляді

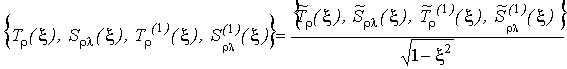, (7)

де – обмежені на [-1, 1] функції.

Наближений розв’язок знаходиться методом граничної колокації [1], який дозволяє звести (6) до системи лінійних алгебраїчних рівнянь. При цьому сингулярні і звичайні інтеграли, які зустрічаються в задачі, обчислюються за допомогою квадратурних формул типу Гауса і механічних квадратур найвищого ступеня точності.

Чисельна реалізація задачі проведена для пластинки і стрижня з фізико-геометричними характеристиками:

, , ν=ν₁=0,3, , , , (8)

при β₀=0.

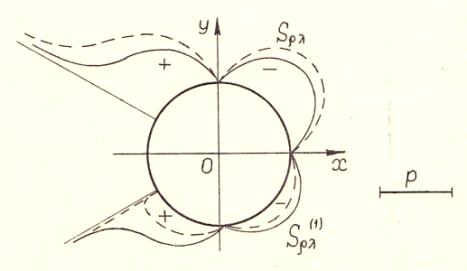
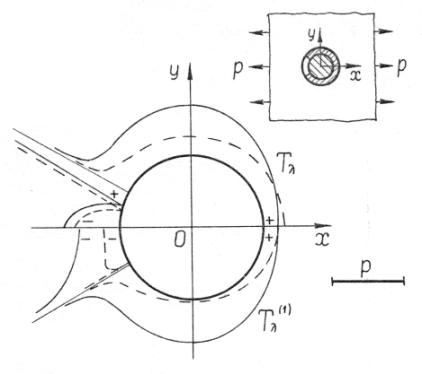
На рис.2 та рис. 3 показано розподіл контактниз зусиль T_ρ, S_ρλ і та кільцевих T_λ і на контурі L₁ при розтязі пластинки зусиллями (Е₀ – модуль пружності матеріалу стрижня).

Рис. 2. Розподіл контактних зусиль на лінії розмежування пластин

Рис. 3. Розподіл кільцевих зусиль на лінії розмежування пластин

Аналіз графіків показує, що вплив кільця на розподіл напружень в пластинках незначний, якщо величини Е₀, Е₁, Е одного порядку. У цьому випадку систему „нескінченна пластинка – кільце – диск” можна замінити системою „нескінченна пластинка – диск”, що призведе до спрощення розв’язку задачі.

Література:

1. Сяський В.А. Напряженное состояние пластины с частично подкрепленным краем // Materialy IV Miedzynarodowej naukowi-praktycznej konferencji “Strategiczne pytania swiatowej nauki – 2008”. Tym 9. Techniczne nauki.: Przemysl. Nauka i studia. – s. 14 – 16.

2. Сяський В.А. Определение порядка сингулярности решения одного класса интегральных уравнений // Materialy IV mezinarodni vedecko-prakticka konference “Vedecke myslene inflacniho stoleti – 2008”. - Dil 13. Matematika. Moderni informacni technologie. Fyzika. Vystavba a architektura: Praha. Publishing House “Education and Science”. – s. 5 – 7.