Voronin V.V., Ibadov S.R., Ibadov R.R., Dmitrienko N.A., Kotlyarova V.V.

Don State Technical University, Shakhty, Russian Federation.

IMAGE RESTORATION USING 2D AUTOREGRESSIVE TEXTURE MODEL AND STRUCTURE CURVE CONSTRUCTION

ABSTRACT

In this paper an image inpainting approach based on the construction of a composite curve for the restoration of the edges of objects in an image using the concepts of parametric and geometric continuity is presented. It is shown that this approach allows to restore the curved edges and provide more flexibility for curve design in damaged image by interpolating the boundaries of objects by cubic splines. After edge restoration stage, a texture restoration using 2D autoregressive texture model is carried out. The image intensity is locally modeled by a first spatial autoregressive model with support in a strongly causal prediction region on the plane. Model parameters are estimated by Yule-Walker method. Several examples considered in this paper show the effectiveness of the proposed approach for large objects removal as well as recovery of small regions on several test images.

Keywords: image inpainting, edge reconstruction, spline interpolation, texture synthesis, autoregressive model, research methodology.

Image inpainting or image reconstruction is an important topic in image processing. The main goal of image inpainting is to restore missing area of “empty” pixels using an information from the outside of the damaged domain. Digital inpainting serves a wide range of applications, such as removing text and logos from still images or videos, reconstructing scans of deteriorated images by removing scratches or stains, or creating artistic effects. This problem is also especially valuable in computer vision systems for image editing and recovery of missing blocks in image coding.Most of image reconstruction methods can be classified into the following groups based on geometry, statistics, sparsity, exemplars and edges methods. The following models of images are used in image inpainting: bounded variation image model, local inpainting, total variation models, curvature-driven diffusions model and Markov random fields model. All these models are used in the methods which compute an optimal solution based on partial differential equations (PDE).

The purpose of this work is to modify our previous algorithm in [1] order to overcome all above mentioned drawbacks. We introduce a novel algorithm for automatic image inpainting based on 2D autoregressive texture model and structure curve construction. In this case any image can be divided into several areas such as texture regions and edges on the local geometric features and different spatial configuration. An image inpainting approach based on the construction of a composite curve for the restoration of the edges of objects in an image using the concepts of parametric and geometric continuity is presented. It is shown that this approach allows to restore the curved edges and provide more flexibility for curve design in damaged image by interpolating the boundaries of objects by cubic splines. After edge restoration stage, a texture restoration using 2D autoregressive texture model and exemplar-based method are carried out. In this paper we propose an algorithm to represent and reproduce texture regions based on the estimation of spatial autoregressive processes. The image intensity is locally modeled by a first spatial autoregressive model with support in a strongly causal prediction region on the plane. Model parameters are estimated by Yule-Walker method.

We summarize the algorithm in the following scheme (Fig. 1).

1. Segmentation using Chan–Vese (CV) model

The image around missing area in our scheme is segmented by the Chan–Vese (CV) model which solves the minimization of the energy functional.

2. Edges analysis and restoration using cubic splines

For the cubic spline interpolation of each of the pairs of parts of the curves the concepts of parametric and geometric continuity are used. For the resulting pairs of points and on the edge in the true image and non-zero tangent vectors and , the cubic Hermite curve is determined.

3. The choice of the boundary pixel by fast marching method

The fast marching method is used in order to select a restored pixel in the area , based on the solution of Eikonal equation in and on the border , where the solution of the equation is the distance map of pixels to the boundary.

4. Texture restoration using 2D autoregressive texture model

After edge restoration stage, a patch restoration using 2D autoregressive texture model is carried out. The image intensity is locally modeled by a first spatial autoregressive model with support in a strongly causal prediction region on the plane.

5. Modified exemplar-based method

The texture in our scheme is restored by an exemplar-based method. Around the pixel selected by fast marching method, a patch is defined. In the next step, on the true image the patches are found for which the Euclidean distance is minimal.

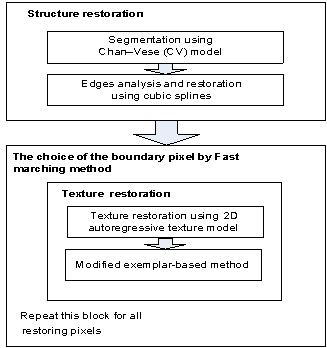
Figure 1. The proposed inpainting algorithm

The effectiveness of the presented scheme is verified on the test images with missing pixels, which are on the borders with the intensity changes in brightness. After applying the missing mask, all images have been inpainted by four different methods. In Figures 2-3 examples of image restoration (a - the original image, b - the image with a missing pixels, c - the image reconstructed by the Navier-Stockes, d - the image reconstructed by the Telea, e - the image reconstructed by the EBM, f - the image reconstructed by the proposed method) are shown.

a) b) c)

d) e) f)

Figure 2. Examples of image restoration

a) b) c)

d) e) f)

Figure 3. Examples of image restoration

To compare the reconstruction images objective quality criteria have been used. Table 1 shows numerical comparison of methods, in terms of quality metric . It is worth noting that the error values confirm the visual analysis. The proposed method provides smaller reconstruction errors, on average 90% less than the processing of other techniques.

Table 1. Comparison of RMSE for test images.

Navier-Stockes	Telea	EBM	Proposed method
0,1239	0,1232	0,1014	0,0654

The paper presents an image inpainting algorithm based on the texture and structure reconstruction of images. This is achieved due to a separate reconstruction of a composite curve for the restoration of the edges of objects in an image and texture synthesis using 2D autoregressive texture model. The image intensity is locally modeled by a first spatial autoregressive model with support in a strongly causal prediction region on the plane. Several examples presented in this paper demonstrate the effectiveness of the algorithm in restoration of different areas of the test images having different geometrical characteristics.

REFERENCES

[1] Voronin, V., Marchuk, V., Sherstobitov, A. and Egiazarian, K., "Image inpainting using cubic spline-based edge reconstruction," Proceedings of SPIE, vol. 8295 (2012).

[2] Котлярова В. В., Формирование методологической культуры магистрантов в процессе освоения курса " История и методология науки " Философия в техническом вузе Сборник научных трудов 6-й Международной научно- практической конференции. СПГПУ. С. 52-54, (2012).

[3] Chan, T. F., Vese, L.A., "A Multiphase level set framework for image segmentation using the Mumford and Shah model," International Journal of Computer Vision, vol. 50(3), pp. 271–293, (2002).

[4] Criminisi, A., Perez, P., Toyama, K., "Region filling and object removal by exemplar-based image inpainting," IEEE Trans. Image Process, vol. 13(9), pp. 28-34 (2004).

[5] Voronin, V.V., Marchuk, V.I. and Egiazarian, K.O., "Images reconstruction using modified exemplar based method," Proceedings of SPIE, vol. 7870 (2011).

[6] Bugeau, A. and Bertalmio, M., "Combining texture synthesis and diffusion for image inpainting," in International Conference on Computer Vision Theory and Applications, vol. 123-132 (2009).