Современные информационные технологии.
Вычислительная техника и программирование
К.т.н.
Дюнова Д. Н., асп. Макоева А. К.
Северо-Кавказский
горно-металлургический институт
(Государственный
технологический университет), Россия
Simulink-модель технологического
комплекса
«Гидрометаллургическое производство цинка»
Современное гидрометаллургическое
производство цинка - технологический комплекс
с полным производственным циклом товарной продукции, целью функционирования которого
является получение продукта заданного качества при минимальных затратах с
возможно меньшим количеством отходов. Различие в сортаментах перерабатываемого
сырья, определяющееся разнообразием минерального и гранулометрического состава,
приводит к различным условиям и режимам переработки. В таких условиях
рациональным путем решения проблемы оптимизации технологических режимов
гидрометаллургического комплекса и обеспечения устойчивой его работы является использование
метода математического моделирования.
Однозначную зависимость
между входными, управляющими и выходными параметрами исследуемого комплекса в
явном виде получить достаточно сложно из-за наличия множества рециклических
потоков. Проведенная на основе технологического принципа декомпозиция комплекса
позволила сформировать в его структуре отдельные подсистемы и выполнить анализ
их параметрической взаимосвязи. В качестве подсистем комплекса выделены основные
переделы цинкового производства. Последовательно расположенные переделы
обмениваются полупродуктами от предыдущего передела к последующему, обусловливая
зависимость выходных параметров комплекса в целом от качественных показателей
сырья и промежуточных продуктов.
Наиболее полное представление о функционировании
технологической системы дает математическая модель, основанная на описании
физико-химических явлений, характерных для ее элементов [1]. Вследствие этого
каждый передел производственного комплекса возможно рассматривать в виде
многомерного технологического оператора. Его символическая математическая
модель может быть выражена следующей зависимостью:
, (1)
где 
- вектор-столбец параметров выходных потоков; 
- нелинейная
вектор-функция; 
- вектор столбец
параметров входных потоков; 
- вектор конструкционных
технологических параметров аппаратов или элементов; n(m)-число параметров
входных (выходных) потоков; p-число
параметров i-го элемента.
Зависимость (1) для каждого элемента системы
представляет собой систему нелинейных алгебраических или дифференциальных
уравнений большой размерности. Если для j-го
элемента системы в выражении (1) вектор-функция 
является линейной
функцией вектора параметров входных потоков 
, то модель этого элемента может быть записана в следующей
форме:
,
(2)
где 
- матрица преобразования j-го
элемента.
Каждый элемент Аmn матрицы преобразования - это некоторый коэффициент функциональной связи, величина
которого не зависит от параметров входного потока и является функцией
конструкционных и технологических параметров данного элемента системы. В
соответствии с видом матрицы преобразования 
можно выделить
следующие типы элементов схемы цинкового производства: операции химического
превращения, разделения потоков, смешения потоков.
Взаимодействие отдельных технологических операторов
(элементов) производственной системы осуществляется благодаря наличию
технологических связей. Технологической
системе комплекса можно поставить в соответствие материальный потоковый граф,
гомоморфный рассматриваемой системе и являющийся некоторой топологической моделью
физических потоков данной системы (рис. 1).
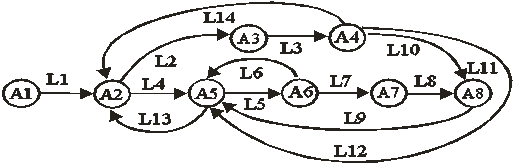
Рис. 1. Граф технологической схемы
цинкового производства
Вершины графа соответствуют
переделам технологической схемы комплекса, трансформирующим общие массовые
расходы физических потоков, дуги отвечают материальным потокам. На рисунке приняты обозначения: А1 – обжиг
цинковых концентратов, А2 – нейтральные выщелачивание огарка и сгущение
нейтральной пульпы, А3 - цементационная очистка нейтральных растворов, А4 –
электролиз цинковых растворов; А5 – кислое выщелачивание пульп и сгущение
кислых пульп, А6 – отмывка, фильтрация и сушка цинковых кеков, А7 – вельцевание
цинковых кеков, А8 – переработка вельц-окислов; L1 – L14 – потоки технологических сред.
К настоящему времени
накоплен значительный опыт в области построения математических моделей
процессов цинкового производства для исследования, определения оптимальных
режимов, применения в системах управления. Анализ известного математического
описания в условиях рассматриваемой задачи показал преимущество балансовых моделей,
позволяющих определять количественные характеристики процессов исследуемого
комплекса, оценивать производительность, определять причины и источники
материальных потерь. Для каждого технологического процесса исследуемого
комплекса сформулированы технологические цели и выделены существенные группы
параметров, разработаны математические модели [2-6].
Основу полученных моделей
переделов комплекса составляют уравнения материального баланса по общему
массовому расходу физических потоков и по массовому расходу компонентов
потоков. На основе математического описания отдельных подсистем построена
математическая модель комплекса в целом [7]. Ее программная реализация в вычислительной
среде Simulink (MATLAB) показана на рис. 2.
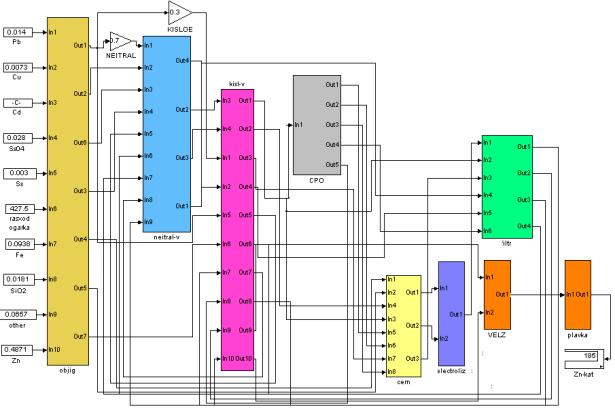
Рис. 2. Simulink-модель
технологического комплекса производства цинка
Адекватность
математического описания исследуемого комплекса установлена на основе
экспериментальных данных, полученных в условиях ОАО «Электроцинк». Полученная
модель цинкового производства может быть использована в задачах оперативного
управления, оптимизации его функционирования, при проектировании новых и
совершенствовании существующих систем управления.
Список
литературы