ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ ТЕХНОЛОГИИ MPI НА ПРИМЕРЕ РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА

ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ ТЕХНОЛОГИИ MPI НА ПРИМЕРЕ РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА

Есеев Е., Нуржумаев О.Н.

Казахский экономический университет имени Турара Рыскулова

erlik_es@mail.ru.

Аңдатпа

Берілген мақалада Лаплас теңдеуіне қойылған Дирихле есебін үшін Якоби әдісін пайдаланып сандық шешімі табылды. Екі өлшемді Лаплас теңдеуі шешу үшін деректердi 1D және 2D декомпозициялану тәсiлдерi пайдаланылып, параллельдеп есептеу алгоритмi құрылды және бағдарламасы арқылы нақты нәтижелер алынды. Сонымен қатар MPI технологиясын пайдаланылып параллельдік есептеудің тізбектей есептеуден артықшылығы мен тиімділігі көрсетілді. Пайдаланылған алгоритм бойынша Лаплас теңдеуінің классына кiретiн басқада осы тектес есептердi шығаруға болады.

Түйінді сөздер: Лаплас теңдеуі, деректер декомпозициясы, параллельдік алгоритм, MPI.

Аннотация

В данной статье рассмотрена решение задачи Дирихле для уравнения Лапласа методом Якоби. Разработан параллельный вычислительный алгоритм используя методы одномерной и двумерной декомпозиции данных и получены результаты вычисления. Показаны преимущества и эффективность параллельного вычисления использующее технологию MPI над последовательной программой. Используя данный алгоритм можно решить и другие уравнение входящие в класс уравнения Лапласа.

Ключевые слова: уравнение Лапласа, декомпозиция данных, параллельный алгоритм, MPI.

Abstract

In this article given the solution of the Dirichlet problem for the Laplace equation by Jacobi method. A parallel computing algorithm using one-and two-dimensional methods of data decomposition and calculation results are obtained. The advantages and effectiveness of parallel computation using MPI technology over sequential program are shown. Using this algorithm can solve the equation, and other members of the class of the Laplace equation.

Keywords: Laplace equation, data decomposition, parallel algorithm, MPI.

1. Введение

В природе многие физические процессы описываются дифференциальными уравнениями. Известно, что не все эти уравнения решаются аналитическим способом. Поэтому, при решении таких задач используют численные методы, такие как метод конечных разностей, метод контрольных объемов и метод конечных элементов. Использование параллельных технологии при решении такого рода задач намного увеличивает эффективность расчета, что показано в данной статье и является основной частью данной работы.

Развитие информационных технологии играет большую роль при компьютерном моделировании сложных физических процессов, которые описываются дифференциальными уравнениями. Так как, параметры вычисления, такие как точность, время расчета, погрешности и.т.д. можно улучшить используя современные технологии.

2. Постановка задачи и ее численное решение

Такие стационарные процессы, как теплопроводность, колебания, диффузия, описываются уравнениями эллиптического типа. Наиболее распространенным уравнением данного типа является уравнение Лапласа:

Рассмотрим задачу Дирихле для двумерного уравнения Лапласа[1], заданную на декартовом произведении D=[0,1]×[0,1]:

(1)

где u = u(х,у) - искомая функция, с начальными и граничными условиями первого рода:

Запишем уравнение (1) в разностном виде[2,3]:

+ = (2)

Наиболее применяемый метод для численного решения уравнения Лапласа является метод конечных разностей. В данном методе область решения представляется в виде равномерной сетки узлов. Так, например, прямоугольная сетка в области может быть задана в виде (рисунок 1):

Рисунок 1 - Метод сеток для двумерной задачи Дирихле

Одним из методов последовательного решения данной задачи является метод Якоби (схема «крест»). Выбирается начальное значение , и пошагово находятся значение на узловых точках при помощи следуюшей формулы:

(3)

Используя данный метод, значение в каждой узловой точки находиться по формуле (3), то есть, при помощи четырех соседних точек в предыдущем слое. В итоге получаем значение каждой внутренней точки

Вычислительный алгоритм состоит из двух частей:

· определение начального значения;

· опредеоение значении искомой функции в следующих слоях используя итерационную формулу (3).

Вычисление происходит до того момента, пока не выполнится следующее условие[2]:

(4)

3. Параллельный алгоритм

Разделим вычислительную область на несколько подобластей. Вычислении на каждой из подобластей производятся независимо от других, вышеописанным методом Якоби. Но, так как, для расчета нам необходимо значение искомой функции на границе, то необходимо производить обмен граничных данных между подобластями. Задача решается при помощи использования технологии MPI. Время вычисления рассчитывается стандартной функцией MPI - double MPI_Wtime(void).

Так как, алгоритм вычисления данной задачи простой, мы будем использовать метод декомпозиции данных. Массив разделяется на несколько частей, и программный код реализует расчет на разных процессах. В таком случае, каждый процесс работает с частью данных. Есть несколько способов разделения данных. Связь между процессами, точнее схема обмена между граничными данными впрямую зависит от разделения массива. Для эффективности параллельного алгоритма, необходимо минимальность связи между процессами. Двумерные массивы можно разделять в одном (одномерная декомпозиция) или в двух (двумерная декомпозиция) направлениях. На рисунке 1 показаны два вида декомпозиции данных.

Рисунок 2 – Декомпозиция данных (одномерная и двумерная)

На рисунке можно увидеть матрицу разделенную на четыре блока. Каждая область вычисляется на отделном процессе. Границы блоков выполняют обмен данными между процессорами. Если число n/P (Р – количество процессоров) небольшое, то эффективно использовать одномерную декомпозицию, и соответсвенно двумерную, если число большое. Обмен данными в данных случаях показаны на рисунках 2 и 3.

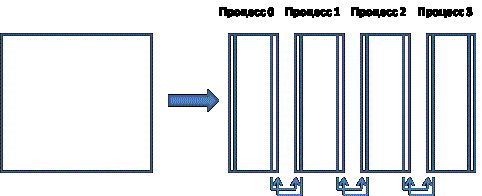
Рисунок 3 – Схема межпроцессорных обменов данными (1D декомпозиция)

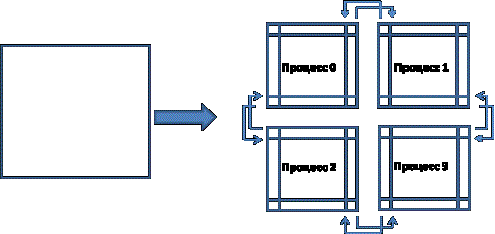
Рисунок 4 – Схема межпроцессорных обменов данными (2D декомпозиция)

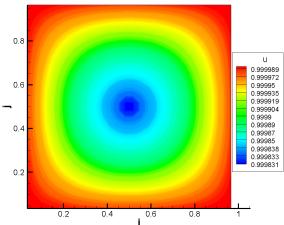
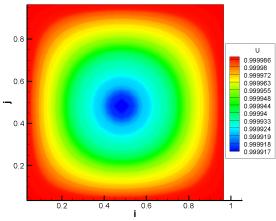
$C:\Users\Math123_2\Desktop\пуассон\12.png$ $C:\Users\Math123_2\Desktop\пуассон\22.png$

а) б)

Рисунок 5 –Результаты вычисления при 1D и 2D декомпозициях

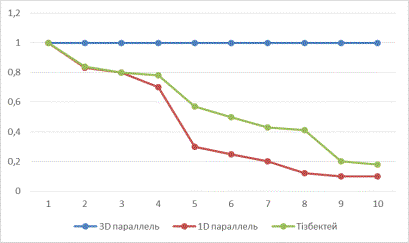
Рисунок 5 – Сравнение эффективностей

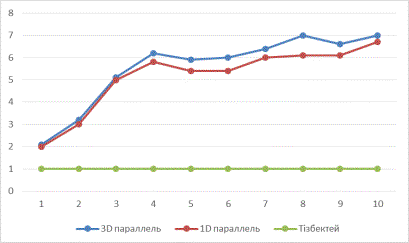
Рисунок 6 – Ускорение параллельного вычисления

4. Заключение

Получены результаты вычисления задачи Дирихле для уравнения Лапласа используя технологию MPI методом 1D и 2D декомпозиции данных. Сравнивая результаты, показана эффективность параллельного вычисления по сравнению с последовательной. На рисунке 6 можно заметить, что при увеличении количества процессов, 2 декомпозиция эффективнее остальных.

Список использованных литератур

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики.-М.: Наука, 1966.

2. Самарский А.А. Введение в численые методы Москва: Наука P. 230.

3. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. -М., Наука, 1972. -368 с.

4. Букатов А. А., Дацюк В. Н., Жегуло А. И. Л Программирование ногопроцессорных вычислительных систем. Ростов-на-Дону. Издательство ООО «ЦВВР», 2003, 208 с.