О НЕКОТОРОЙ ПОСТАНОВКЕ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИЙ ЖИДКОСТИ В УПРУГО-ПОРИСТОМ СРЕДЕ
Bahaerguli Nulahemaiti1), Guo
Jindong1), Ж.Д. Байшемиров2)
1) College of Mathematics and
Statistics in Yili Normal University, Gulja, Ili, Xinjiang, People’s Republic
of China
2) Казахский национальный педагогический университет
им. Абая, г. Алматы, Казахстан
В
настоящей работе рассматривается для простоты плоская задача
фильтрации несмешивающихся жидкостей в области, ограниченной непроницаемыми
подошвой пласта. При приближении пограничного слоя применен метод слабой
аппроксимации. Полученные расщепления могут быть положены в основу построения
ряда разностных схем. Создание математических моделей учитывающих законы фильтрации многофазных
жидкостей в пористых средах направление
приводит к постановкам сложных пространственных задач многофазной фильтрации в
нефтяных пластах. К этому же направлению следует отнести методы решения
модельных задач теории фильтрации применительно к нефтяным пластам.
Математические модели указанного направления предназначены, в первую очередь,
для детального исследования механизмов
вытеснения и очень полезны для теоретического анализа новых технологий.
Ключевые
слова: фильтрация жидкости, пористая среда
1. ВВЕДЕНИЕ
Для обобщенного решения для многомерной задачи
Стефана уравнения теплопроводности для различных фаз трактуются как одно
уравнение:
![]()
где ![]() - удельная внутренняя энергия,
- удельная внутренняя энергия, ![]() -температура и удельная внутренняя энергия есть известная
функция температуры и
-температура и удельная внутренняя энергия есть известная
функция температуры и ![]() терпящая разрыв
первого рода при значениях температуры, равной температуре плавления, и
достаточно гладкая всюду вне этой точки. Так как каждое классическое
решение является и обобщенным, то вопрос о единственности классического решения
задачи Стефана был полностью решен. С этого момента центральным стало изучение
структуры обобщенного решения и выяснение условий, при которых обобщенное
решение задачи Стефана будет классическим. Естественно было ожидать, что если в
начальный момент времени в рассматриваемой области состояние среды двухфазное,
присутствует только жидкая и твердая фазы, разделенные гладкой поверхностью, то
обобщенное решение задачи Стефана совпадает с классическим [1]. Для случая многих
пространственных переменных существование классического решения в малом по
времени было доказано [2].
терпящая разрыв
первого рода при значениях температуры, равной температуре плавления, и
достаточно гладкая всюду вне этой точки. Так как каждое классическое
решение является и обобщенным, то вопрос о единственности классического решения
задачи Стефана был полностью решен. С этого момента центральным стало изучение
структуры обобщенного решения и выяснение условий, при которых обобщенное
решение задачи Стефана будет классическим. Естественно было ожидать, что если в
начальный момент времени в рассматриваемой области состояние среды двухфазное,
присутствует только жидкая и твердая фазы, разделенные гладкой поверхностью, то
обобщенное решение задачи Стефана совпадает с классическим [1]. Для случая многих
пространственных переменных существование классического решения в малом по
времени было доказано [2].
2. МЕТОДИКА
Общий подход к описанию процесса массообмена и
диффузии изложены в работах [3, 4]. При этом уравнения для определения
скорости вещества, ассоциированного с жидкой фазой, закон его сохранения
записывается в виде [8]:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
где ![]() - массовая
скорость вещества, с и N - массовые концентрации вещества в
жидкой и твердой фазах, т -
пористость, D - коэффициент конвективной диффузии, учитывающий
молекулярной диффузии,
- массовая
скорость вещества, с и N - массовые концентрации вещества в
жидкой и твердой фазах, т -
пористость, D - коэффициент конвективной диффузии, учитывающий
молекулярной диффузии, ![]() -скорость
фильтрации. Для замыкания системы (2.1) и (2.2) используются изотермы обмена
веществом между жидкой и твердой фазами [4]:
-скорость
фильтрации. Для замыкания системы (2.1) и (2.2) используются изотермы обмена
веществом между жидкой и твердой фазами [4]:
![]()
![]() (2.3)
(2.3)
К системе (2.1)-(2.3)
присоединяется уравнение фильтрации, которое записываем в виде:
![]() (2.4)
(2.4)
и уравнение неразрывности фильтрата:
![]() (2.5)
(2.5)
Тем не менее, на конец замыкается с помощью
уравнений состояния:
![]()
![]() (2.6)
(2.6)
где k - коэффициент проницаемости, μ, р - вязкость и плотность фильтрата, р - давление, Кm, Кc - модуль сжимаемости, заполнителя (жидкой фазы) и
твердого скелета. Уравнение (2.1) - (2.6) образуют систему для определения этих неизвестных:
![]()
![]()
![]() и
и ![]()
В случае постоянных k и μ, система
(2.1) - (2.3) с неизвестными ![]() может
рассматриваться независимо от уравнений фильтрации (2.4)-(2.6). Тогда задача
диффузии и массообмена решается после определения скорости фильтрации
может
рассматриваться независимо от уравнений фильтрации (2.4)-(2.6). Тогда задача
диффузии и массообмена решается после определения скорости фильтрации ![]() , т.е. после
решения соответствующей задачи фильтрации.
, т.е. после
решения соответствующей задачи фильтрации.
3. ОСНОВНАЯ ЧАСТЬ
Далее рассмотрим стационарный пример плоско-радиальной
фильтрации, в случае которого закон и уравнение баланса массы вещества при
постоянной пористости дают:
![]() (3.1)
(3.1)
Так значить, что дальнейшее упрощение уравнения (3.1) зависит от
отношения скоростей фильтрации жидкости и молекулярной диффузии
ассоциированного с ней вещества [3,5], т.е. от
числа Пекле: ![]() ,
,
где d
- характерная длина. Уравнение (3.1) при D=const в безразмерном виде перепишем:
![]() (3.2)
(3.2)
При ![]() ;
; ![]() ламинарном
течении жидкости можно рассматривать характерные интервалы числа
ламинарном
течении жидкости можно рассматривать характерные интервалы числа ![]() .
.
І) ![]() - диффузия
имеет чисто молекулярный характер. Тогда уравнение (3.1) в размерных переменных
записывается так:
- диффузия
имеет чисто молекулярный характер. Тогда уравнение (3.1) в размерных переменных
записывается так:
![]() ,
, ![]() (3.3)
(3.3)
ІІ) ![]() - скорости
фильтрации значительные, тогда имеем:
- скорости
фильтрации значительные, тогда имеем:
![]() (3.4)
(3.4)
Далее рассмотрим случай ![]() . Можно
считать, что процесс фильтрации происходит в результате поступления постоянного
объема фильтрата в пласт за время t = Т, после которого устанавливается стационарный режим
фильтрации, и продуктивный пласт разделяется на две зоны [6]. В первой зоне
. Можно
считать, что процесс фильтрации происходит в результате поступления постоянного
объема фильтрата в пласт за время t = Т, после которого устанавливается стационарный режим
фильтрации, и продуктивный пласт разделяется на две зоны [6]. В первой зоне ![]() (r -
радикальная координата с началом в центре скважины, Rc -радиус скважины) происходит диффузия и интенсивный
массообмен вещества с жидкой и твердой фазами горной породы (пластовой среды). Границу этой зоны считаем постоянной
и равной r = R1. Вторая
зона не занята фильтратом, поэтому проникновение фильтрата здесь определяется
только диффузией. Уравнение для определения концентрации диффундирующего
вещества записываем в виде:
(r -
радикальная координата с началом в центре скважины, Rc -радиус скважины) происходит диффузия и интенсивный
массообмен вещества с жидкой и твердой фазами горной породы (пластовой среды). Границу этой зоны считаем постоянной
и равной r = R1. Вторая
зона не занята фильтратом, поэтому проникновение фильтрата здесь определяется
только диффузией. Уравнение для определения концентрации диффундирующего
вещества записываем в виде:
![]() (3.5)
(3.5)
где ![]() -скорость фильтрации пластовой
жидкости, с1-концентрация
диффундирующего вещества [7]. В условиях массообмена между фильтратом и твердой
фазой к уравнению (3.4) необходимо добавить уравнение кинетики, где в случае
преобладания адсорбционного процесса выражения для скорости внешнего обмена
возьмем в виде:
-скорость фильтрации пластовой
жидкости, с1-концентрация
диффундирующего вещества [7]. В условиях массообмена между фильтратом и твердой
фазой к уравнению (3.4) необходимо добавить уравнение кинетики, где в случае
преобладания адсорбционного процесса выражения для скорости внешнего обмена
возьмем в виде: ![]() , где
, где ![]() -константы скорости адсорбции,
-константы скорости адсорбции, ![]() -концентрация равновесия количеству вещества,
поглощенному к данному моменту времени твердой фазой; эта концентрация связана
с количеством сорбированного вещества N -
уравнением изотермы
-концентрация равновесия количеству вещества,
поглощенному к данному моменту времени твердой фазой; эта концентрация связана
с количеством сорбированного вещества N -
уравнением изотермы ![]()
При необратимом массообмене принимается ![]() =0. В дальнейшем рассмотрим случай необратимого массообмена и уравнение (3.4) записываем в виде:
=0. В дальнейшем рассмотрим случай необратимого массообмена и уравнение (3.4) записываем в виде:
![]() (3.6)
(3.6)
Скорость фильтрации определяем из закона Дарси: ![]() , где
, где ![]() , и
, и ![]() - скорости фильтрации соответственно в зонах
- скорости фильтрации соответственно в зонах ![]() и
и ![]() ,
, ![]() ,
, ![]()
![]() - соответствующие значения проницаемости и вязкости
фильтрата и пластовой жидкости. Rk-радиус контура питания,
- соответствующие значения проницаемости и вязкости
фильтрата и пластовой жидкости. Rk-радиус контура питания, ![]() и
и ![]() - давление в соответствующих зонах, удовлетворяющие
уравнением:
- давление в соответствующих зонах, удовлетворяющие
уравнением: ![]() при
при ![]() и
и ![]() при
при ![]() и граничным условиям и условиям сопряжения:
и граничным условиям и условиям сопряжения: ![]() при
при ![]()
![]() при
при ![]() ;
; ![]() и
и ![]() при
при ![]() . Таким
образом, имеем:
. Таким
образом, имеем: ![]()
![]() ,
,
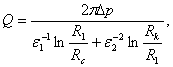
![]()
![]()
Тем не
менее, скорости фильтрации в каждой
зоне будут равны: ![]()
![]()
![]() . Поскольку подставляя
. Поскольку подставляя ![]() и
и ![]() , мы окончательно
получаем:
, мы окончательно
получаем:
![]() ,
,![]()
![]() (3.7)
(3.7)
Решение уравнений (3.7), удовлетворяющих условием ![]() при
при ![]() ,
, ![]() при
при ![]() , получим методом
преобразования Лапласа по времени:
, получим методом
преобразования Лапласа по времени:
![]() ,
, ![]() (3.8)
(3.8)
где ![]() -функция Хевисайда,
-функция Хевисайда, ![]()
![]()
![]() ,
, ![]() .
.
Без учета смещения фильтрата раствора с пластовой жидкостью
(например, нефтью) концентрация вещества равна нулю соответственно за фронтами
вытеснения ![]() и
и ![]() и изменяется по
экспоненциальному закону перед фронтом
и изменяется по
экспоненциальному закону перед фронтом ![]() и постоянная
и постоянная ![]() перед фронтом
перед фронтом ![]() .
.
Функция ![]() - концентрацию вещества на адсорбенте (скелет породы)
находим по формуле
- концентрацию вещества на адсорбенте (скелет породы)
находим по формуле ![]() которая дает:
которая дает: ![]()
где 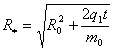 на поверхности
скважине
на поверхности
скважине ![]() , имеем:
, имеем: ![]() .
.
Всего этого следует, что полученное решение справедливо только
до начала предельного насыщения поверхности ![]() , т.е. при
, т.е. при ![]() (
(![]() величина предельного
насыщения) причем
величина предельного
насыщения) причем ![]() . При
. При ![]() следует
учитывать влияние контура пласта на процесс [9].
следует
учитывать влияние контура пласта на процесс [9].
4. ЗАКЛЮЧЕНИЕ
Можно условно принять, что технология вскрытия пласта включает в
себя следующие управляемые элементы: способ бурения, режим бурения режим
промывки, тип и компонентный состав бурового раствора, промежуток времени от
момента полного вскрытия продуктивного пласта до момента начала цементирования. Аналогично следует принять, что технология освоения
скважин включает в себя элементы: способ крепления, способ перфорации, способ
вызова притока жидкости из пласта.
Список
литературы
1. Etthey D.R. A finity difference scheme for melting problems // J. Inst.
Math. Appl. - 1974. – Vol. 13. - P.353-366.
2. Meirmanov, A.M., 1986. Stefan Problem. Novosibirsk, Nauka, pp: 239.
3. Коновалов А. Н. Задачи
фильтрации многофазной несжимаемой жидкости. - Новосибирск: Наука, 1988. - 166
с.
4. Пеньковский В. И.
Капиллярное давление, гравитационное и динамическое распределение фаз в системе
«вода-нефть-газ-порода» // Прикладная механника и тех. физика. - 1996. - №6. -
С.20-30.
5. Жумагулов Б.Т., Зубов
Н.В., Монахов В.Н., Смагулов Ш.С. Новые
компьютерные технологи в нефтедобыче. - Алматы: Гылым, 1996. - 167 с.
6. Barenblatt, G.I., T.W. Patzek and D.B. Silin, 2002. The Mathematical
Model of Non Equilibrium Effects in Water-Oil Displacement. Paper SPE 75169
presented at SPE/DOE Improved Oil Recovery Symposium, Tulsa, Oklahoma, 13-17 of
April 2002.
7. Бочаров О.Б., Телегин
И.Г. Числовое моделирование термокапиллярного противоточного напитывания //
Термо физика и аэромеханика. – 2005.
– № 12. –Р. 33.
8. Meirmanov, A.M., A description of seismic
acoustic wave propagation in porous media via homogenization. SIAM J. Math. Anal. 40 (2008), No. 3, 1272–1289.
9. Mukhambetzhanov, S.T. and Baishemirov, Zh. D., 2013. Procedure of
Evaluation Development for Drilling-in and Well Completion. World Applied Sciences Journal 24 (2):
168-174. http://dx.doi.org/10.5829/idosi.wasj.2013.24.02.13172