МАТЕМАТИКА/1.Дифференциальные и интегральные уравнения

Dokukova N.A., Kaftaikina E.N., Zenkovich V.V.

Belarusian state university, Belarus

General patterns of improper vibrations of dynamical systems with an arbitrary number of degrees of freedom

This article presents a calculation method of improper vibrations dynamic systems with an arbitrary number of degrees of freedom by reducing the system of linear -bonded non-homogeneous second order differential equations to -independent from each other differential equations of 2-order. Obtained general results allow to determine the criteria for the selection of rational physical and geometrical parameters of the original mechanical system based on sustainability and quality of the dynamic model [1-5].

Vibrations of mechanical systems with degrees of freedom equal to the system represented in the form of -linear second order differential equations:

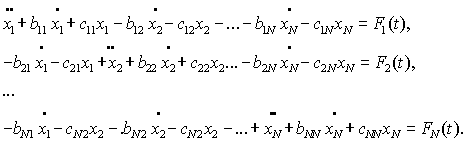(1)

Introduce the notations similar to those shown in [1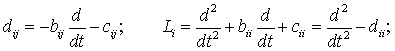, 2]

(2)

Then (1) in the new notation, (2) can be rewritten as follows:

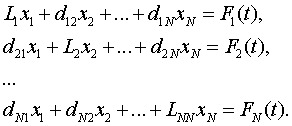(3)

It can be represented in matrix form:

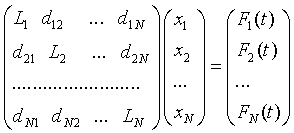(4)

Matrix elements are linear differential operators (2).

System (1) can be reduced to a system of independent linear ordinary differential equations of 2N-order disconnected to each other using certain non-singular linear transformations:

. (5)

The right side consists of a combination of functions and their derivatives.

Linear differential operator of the following form is on the left side of each new differential equation:

, (6)

is the determinant of the system (1)

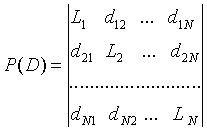. (7)

The right side of the equations system (5) are functions , determined by the determinants of matrices.

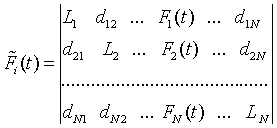, (8)

The i-th column consists of functions , taken from (1), at the other places are the elements of the system (4).

Inhomogeneous linear differential equation of 2N-order is obtained for each unknown variable , independent of other unknown variables, found from the system of equations (3) using form (4), which can be rewritten as follows:

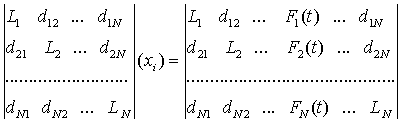. (9)

The differential operators can be considered as elements belonging to a commutative ring . Such ring would be the space of differential operators of the form , where - real numbers, and - differential operator. Elements of the determinant (9) are linear differential operators, which have algebraic properties due to their linearity and differentiability. Adoption (9) follows directly from Cramer's rule for linear systems of algebraic equations. Prove this assumption.

Put - twice continuously differentiable function defined on an interval , such that, when substituted into equations (1), it becomes an identity:

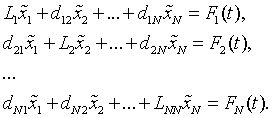(10)

Multiplying the first equation of (10) by the cofactor of the element in the main matrix of the system, then multiply the second equation by , the third by and so on. Sum up all these equalities. The result is the following relationship:

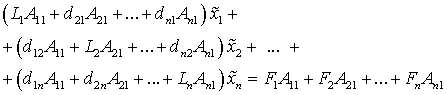. (11)

Then the operator at is equal to the determinant of the main system matrix, operators at the other is equal to the zero operator on the basis of the known algebraic equation

.

A solution of equation (11) is the equation, which determines the desired unknown function

. (12)

Using the same method differential equations are obtained for the other functions , from equations (9).

Linear transformation of differential equations allows us to pass from a connected system of linear equations (1) to an equivalent system of disconnected linear equations, but higher order

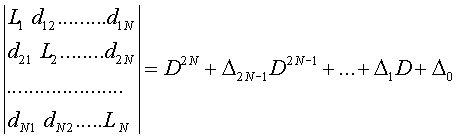(13)

Having at the left side of the equation a polynomial with coefficients that are some combination coefficients of the original system (1).

As an example, consider a model with six degrees of freedom and the following initial conditions:

x₁(t) = 0.5, x₂(t) = 0.5, x₃(t) = 0.8, x₄(t) = 0.3, x₅(t) = 0.04, x₆(t) = 0.2,

x₁¢(t) = 1.04, x₂¢(t) = 2.3, x₃¢(t) = 3.07, x₄¢(t) = 1.6, x₅¢(t) = 1.002, x₆¢(t) = 2.5.

Introduce additional notation:

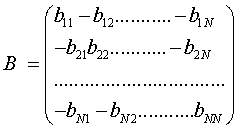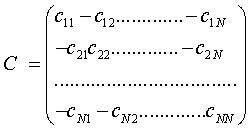, (14)

Then the system (1) in matrix form becomes:

, (15)

Matrix elastic and damping coefficients of the canonical representation (14) is the following

,

,

.

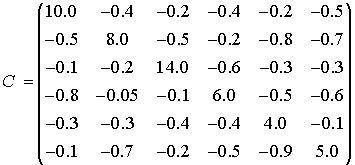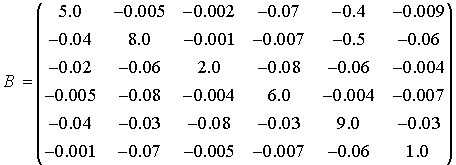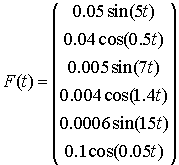Find the solution of six non-connected with each other differential equations - improper vibrations of a dynamical system with six degrees of freedom (15) in the general form using obtained the general system of - independent differential equations of order represented by (5):

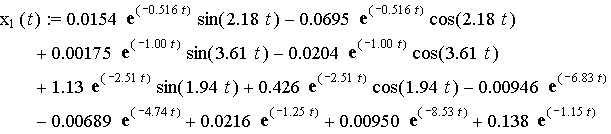
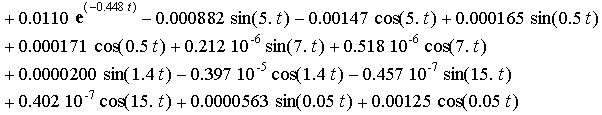
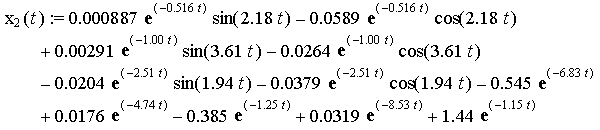
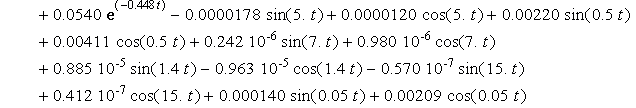
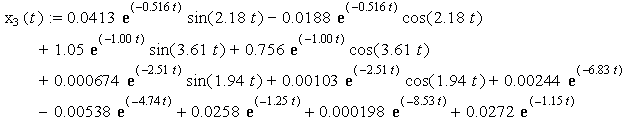
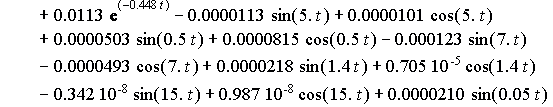
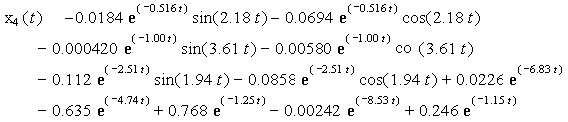
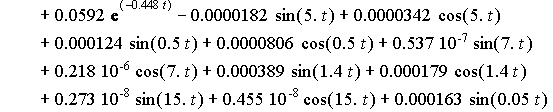
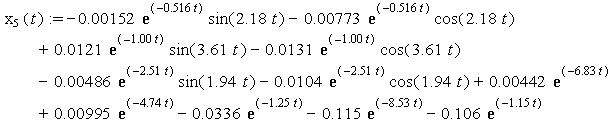
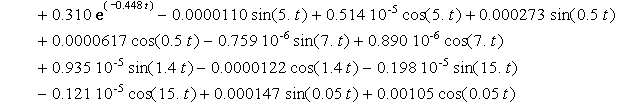
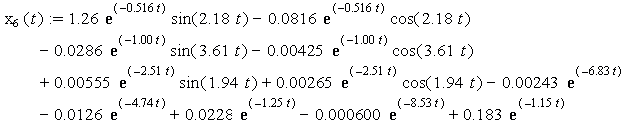
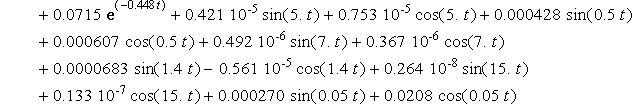
Charts of analytic solutions of inhomogeneous differential equations (15), describing the oscillations of a system with six degrees of freedom are shown in Figure 1 and Figure 2 for the time interval from 0 seconds to 15 seconds.

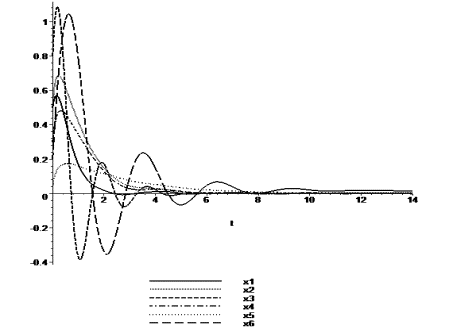
Figure 1 - Accurate analytical solutions of inhomogeneous differential equations corresponding to the time of acceleration of the mechanical system

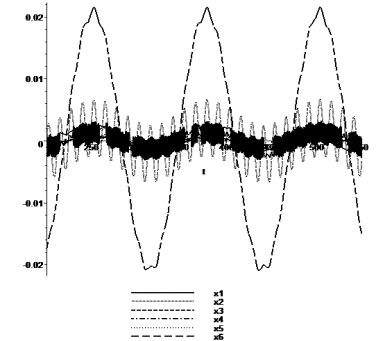
Figure 2 - Accurate analytical solutions of inhomogeneous differential equations in the interval seconds, corresponding to the steady state of a mechanical system

The system of six related non-homogeneous differential equations with separable variables is integrated analytically. Accurate theoretical results of its own and forced vibrations are obtained using the known initial velocity and displacement data provided by the method.

References:

1. N. A. Dokukova and P. N. Konon Generalities of passive vibration dampers isolating vibrations// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 2, Pages 412-417, Publisher Springer New York, ISSN: 1062-0125.

2. N. A. Dokukova and P. N. Konon General laws governing in mechanical vibratory systems// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN: 1062-0125.

3. N. A. Dokukova, M. D. Martynenko and E. N. Kaftaikina Nonlinear vibrations of hydraulic shock absorbers// Journal of Engineering Physics and Thermophysics, 2008, Volume 81, Number 6, Pages 1197-1200, Publisher Springer New York, ISSN: 1062-0125.

4. N. A. Dokukova, P. N. Konon and E. N. Kaftaikina Nonnatural vibrations of hydraulic shock-absorbers// Journal of Engineering Physics and Thermophysics, 2008, Volume 81, Number 6, Pages 1191-1196, Publisher Springer New York, ISSN: 1062-0125.

5. N. A. Dokukova, P. N. Konon On the equivalence of the methods of impedance and amplitude-frequency characteristics for the study of oscillations in a gyro dampers // Journal of Engineering Physics and Thermophysics, 2003. Volume 76, Number 6. Pages 115-118.