Алгебраические основы теории сингулярных возмущений и теорема Пуанкаре о разложении

Качалов В.И.

Россия, Москва, Национальный исследовательский университет Московский Энергетический Институт

Введение. Современная теория сингулярных возмущений, представленная различными асимптотическими методами [1,2,3] в своём развитии всё больше опирается на достижения функционального анализа и алгебры. В данной статье рассмотрена алгебраическая модель этой теории, основанная на общем для теории дифференциальных уравнений утверждении, что всякое дифференциальное уравнение первого порядка порождает гомоморфизм между алгебрами голоморфных функций различного числа переменных и, наоборот, каждому такому гомоморфизму соответствует дифференциальное уравнение. С точки же зрения функционального анализа, важным в теории сингулярных возмущений является вопрос обычной сходимости по степеням малого параметра асимптотических рядов, представляющих решения сингулярно возмущенных задач. Эта проблема решена в рамках метода регуляризации Ломова С.А. с использованием пространств векторов экспоненциального типа [1,5,6]. Асимптотические решение сингулярно возмущенных задач, сходящиеся в обычном смысле Ломовым С. А. были названы псевдоаналитическими [6]. Автор настоящей статьи разрабатывает метод голоморфной регуляризации [7], являющийся логическим продолжением метода регуляризации Ломова С.А.

1. Коммутационные соотношения и гомоморфизмы алгебр голоморфных функций.

Обозначим через алгебру голоморфных в точке функций одной комклексной переменной а, через алгебру функций двух комплексных переменных и w, голоморфных в точке Обе алгебры снабдим топологией индуктивного предела пространств функций, голоморфных в окрестностях, стягивающихся в указанные точки.

Теорема 1.Отображение удовлетворяющее соотношению

причём является непрерывным гоморфизмом алгебры в алгебру и, наоборот, всякий непрерывный гомоморфизм в удовлетворяет коммутационному соотношению (1).

Доказательство. Вначале докажем непрерывность отображения A, удовлетворяющего коммутационному соотношению (1). Для этого рассмотрим последовательность где алгебра функций, голоморфных в некоторой окрестности точки сходящуюся к функции в топологии и, пусть такая окрестность точки что если Здесь, через обозначено множество значений A[z] как функции двух переменных Тогда

и непрерывность отображения доказана.

Пусть теперь отображение подчинено коммутационному соотношению (1) и Тогда,

т.е. является гомоморфизмом алгебры в алебру Наоборот, пусть гомоморфизм алгебры в алебру Имеем,

Отсюда следует, что если

то

Здесь мы воспользовались линейностью и непрерывностью отображения A, а также тем, что Терема доказана.

Покажем, что каждому коммутационному соотношению (1) соответствует вполне определенное дифференциальные уравнение. Для этого обозначим через образ при отображении A, а через образ и дополнительно потребуем, чтобы

Далее, продифференцируем (1) по и w:

и, обозначим

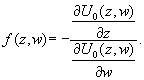
Очевидно, что и Тогда, если второе из этих равенство умножить на и сложить с первым, то получится - уравнение первых интегралов дифференциального уравнения первого порядка в окрестности точки Итак, всякое коммутационное соотношение а, значит, гомоморфизм алгебры в алгебру порождает дифференциальное уравнение и, наоборот, как будет показано в п.2, всякое дифференциальное уравнение первого порядка порождает гомоморфизм.

2. Сингулярно возмущенные задачи и теорема Пуанкаре о разложении. Рассмотрим сингулярно возмущенное при уравнение

с начальным условием

Теорема 2. Пусть правая часть уравнения (2) и Тогда отображения заданные формулой

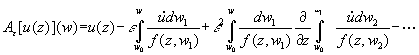
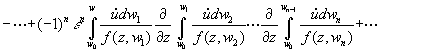
образуют голоморфное в точке семейство непрерывных гомоморфизмов алгебры в алгебру и удовлетворяют коммутационному соотношению при каждом достаточно малом При этом образ состоит из первых интегралов уравнения (2) в некоторой окрестности точки

Доказательство теоремы 2 приведено в [7]. Итак, теорема 2 гарантирует существование голоморфных в точке первых интегралов уравнения (2) и, поэтому можно сказать, что первые интегралы наследуют свойство гладкости левой части уравнения по параметру ( которой входит в уравнение голоморфным, даже целым образом). Само же решение задачи Коши (2),(3) в общем случае не может быть голоморфным в точке поскольку в этой точке теоремы существования не имеют места ввиду отсутствия при самого дифференциального уравнения. Совершенно другая ситуация возникает, когда малый параметр находится в правой части уравнения. В этом случае теорема Пуанкаре о разложении [4] гарантирует существование и единственность голоморфного в точке решение задачи Коши

если голоморфна как функция трех комплексных переменных в точке

Таким образом, в регулярном случае (4) решение голоморфно в точке в сингулярном случае (2),(3) существуют первые интегралы, голоморфные в точке Более того, теорема о существовании голоморфных по параметру первых интегралов имеет глобальный характер. В этом смысле, теорема Пуанкаре получает дальнейшее развитие.

3. Голоморфные решения сингулярно возмущенных задач. Введём следующее понятие.

Определение. Решение задачи (2),(3) называется псевдоголоморфным в точке если оно представимо в виде

где гомоморфная в точке функция, а голоморфна в точке и Если при этом ряд

представляющий функцию сходится в некоторой окрестности точки равномерно где некоторый компакт, содержащий точку а связное множество на комплексной плоскости содержащее бесконечно удаленную точку, то решение называется псевдоголоморфным в глобальном смысле.

Теорема 3. При выполнении условий теоремы 2 задача Коши (2),(3)имеет единственное голоморфное в точке решение.

Эта теорема доказана в [7] с использованием теоремы о неявной функции. Что касается глобальной псевдоголоморфности, то для нее найдены достаточные условия.

Пример. Рассмотрим задачу Коши

имеем в соответствии с формулой (4) первый интеграл при .

С помощью теоремы о неявной функции из общего интеграла получим решение поставленной задачи:

если считать и вещественными, то псевдоголоморфность в глбальном смысле при станет очевидной. При этом

равномерно по на отрезке где

Замечание. Метод голоморфной регуляризации [7] состоит в нахождении функции u(z), обеспечивающей глобальную псевдоголоморфность.

4. Структура особого многообразия, порждаемого точкой Как следует из определения псевдоголоморфности, особое многообразие (пограничный слой), порждаемого точкой описывается коэффициентами ряда

которые не определены в точке С другой стороны, из теоремы Пуанкаре о разложении очевидным образом следует голоморфность решения задачи (2),(3) в любой точке Следовательно, является изолированной особой точкой решения к тому же однозначного характера, поскольку для уравнения (2) выполнены условия единственности решения. Наиболее содержательным в теории сингулярных возмущений нам представляется случай, когда является существенно особой точкой функции (почти при всех

Обозначим через гиперповерхность в заданную уравнением где первый интеград уравнения (2)голоморфный в точке и такой, что Пусть множество из области существование решения для которых является особой точкой

Теорема 4. Для того чтобы точка была существенно особой точкой решения задачи (2),(3) необходимо и достаточно, чтобы при каждом и произвольном точка была предельной точкой гиперповерхности

Доказательство. Необходимость. Пусть точка такова, что является существенно особой точкой решения По теореме Пикара в любой сколь угодно малой окрестности точки функция может принимать все значения, кроме быть может одного. Фиксируем и выберем последовательность так, чтобы Поскольку определяется уравнением то

и, значит, а т.к. то точка является предельной точкой гиперповерхности

Достаточность. Пусть предельная точка гиперповерхности Это означает, что при любом фиксированном существуют последовательности и такие, что т.е. при Но, тогда поскольку определяется из уравнения Итак, при фиксированном функция голоморфная в кольце принимает в точках сколь угодно близких к нулю значения Ввиду произвольности это означает, что не существует, т.е. существенно особая точка решения задачи (2),(3). Перейдем к классификации существенно особых многообразий, порождаемых точкой

Определение. Будем говорить, что точка порождает существенно особое многообразие линейного типа, если решение задачи Коши (2),(3) представимо в виде где и голоморфные в точке

функции, а целая функция комплексной переменной в остальных случаях будем говорить о многообразиях нелинейного типа.

Многообразия линейного типа возникают, как правило, в случае обычной сходимости регуляризованных рядов. При этом функции, описывающие такое многообразие являются элементами пространства векторов экспоненциального типа [5,6], а пограничный слой имеет простую структуру. Однако в большинстве задач математической теории пограничного слоя возникают существенно особые многообразия нелинейного типа.

Заключение. Указанный в статье алгебраический подход настоящее время распространяется на уравнения высших порядков и системы дифференциальных

уравнений.

Литература

1. Ломов С.А. Введение в общую теорию сингулярных возмущений. ---М.: Наука,

1981.

2. Васильева А.Б., Бутузов В.Ф. Асимптотика разложения решений сингулярно

возмущенных уравнений. ---М.: Наука, 1973.

3. Богаевский В.Н., Повзнер А.Я. Алгебраические методы в теории возмущений.

---М.: Наука, 1987.

4. Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений.-М.: Изд-во иностранной литературы. 1958.-475 с.

5. Ломов С.А., Качалов В.И. Гладкость решений дифференциальных уравнений по

сингулярно входящему параметру // ДАН СССР, 1988, т. 299, № 4.

6. Ломов С.А., Качалов В.И. Псевдоаналитические решения сингулярно

возмущенных задач // Доклады РАН, 1994, т. 334, № 6.

7. Качалов В.И. Голоморфная регуляризация сингулярно возмущенных задач //

Вестник МЭИ, № 6, 2010. --- С. 54-62.