Физика/8. Молекулярная физика
к.т.н., доц. Магеррамов М.А.,
Бакинский Государственный Колледж Пищевой Промышленности
Асланова М.С.,
Азербайджанский
Государственный Аграрный Университет
Прогнозирование температурной зависимости
массовой доли вымороженной воды и изобарной теплоемкости ткани плодов граната
Для
моделирования теплофизических характеристик (ТФХ) (кроме теплопроводности) растительного сырья как
функции от температуры достаточно и эффективно используется аддитивное правило,
т. е нужно исходить, прежде всего, из заданного состава сырья и теплофизических
свойств (ТФС) по таким компонентам как вода, сухие вещества, жир т. д.[1,2]. В замо-роженном состоянии
соответственно появляются и дополнительные компо-ненты, как лед и воздух.
Если учесть, что вода имеет наибольшую
среди веществ объемную теплоемкость, а влагосодержание в фруктах и овощах составляет величины от 0.80 до 0.95 (в
гранатах в зависимости от сорта влаги составляет от 0.82 до 0.85)[2], то,
очевидно, что при исследовании ТФХ в процессе холодильной обработки, особенно
для процессов замораживания и размораживания, важно отличать объекты с разным
влагосодержанием. Однако, до настоящего времени свойства переохлажденной воды и
льда в области низких температур недоста-точно изучены, особенно когда жидкая вода
превращается из переохлажден-ного в стекловидное состояние. Результаты
исследований свойств воды в переохлажденном состоянии в ряде работ аппроксимированы
линейными и квадратичными зависимостями (до минус 7°С) явно не отвечают нашим требованиям, поскольку
на изобаре 1 атм температура на спинодали составляет -45°С [3].
В
данной работе мы воспользовались новыми результатами исследования изобарной
теплоемкости переохлажденной воды G. Archer (2000) и C. Bischof (2004) [4,5] в диапазоне ![]() . Формула для расчета изобарной
теплоемкости воды как функция от температуры была получена путем аппроксимации
этих экспериментальных данных методом
наименьших квадра-тов. Она получена в виде полинома (R2=0,996) с целыми и дробными степенями:
. Формула для расчета изобарной
теплоемкости воды как функция от температуры была получена путем аппроксимации
этих экспериментальных данных методом
наименьших квадра-тов. Она получена в виде полинома (R2=0,996) с целыми и дробными степенями:
![]() , (1)
, (1)
где Вi, ![]() - коэффициенты полинома.
- коэффициенты полинома.
B1=14,98992; B2=23,18982;
B3=-1714,94673; B4=14096,98228;
B5=-55893,6937;
B6=125391,0389; B7=-161981,892;
B8= 112360,1438; B9=-31909,7683.
По предложению В. П. Латышева [6] в
более низком температурном диапазоне от
Тэ до 228 К ( 77 К £ Т< 228К) из- за отсутствия эксперименталь-ных данных
по теплоемкости переохлажденной воды принято Св(Т) приблизи-тельно
как квадратичнyю функцию от температуры
Св(Т)=
а+ b·T+c·T2, (2)
a,b,c- коэффициенты; a=4198,4; b=-3,288; c=7,549.10-2 .
Изобарная теплоемкость льда определяется формулой, предложенной в ASHRAE- 2002 [7]
Cл(t) = с+d·t ,
(3)
где Cл(t)-теплоемкость льда, Дж/кг К; с,d -
коэффициенты; с = 2058,4; d = 6,0698; t- температура, оС.
В процессе замораживания мякоти семена
граната по доли вымороженной воды ткани
полученные экспериментальные данные по w(Т) показаны в табл.
Таблица
Экспериментальные данные
по равновесной доли вымороженной
воды в
процессе замораживания мякоти семена граната
|
Температура оС |
w(Т) |
|
0 |
0 |
|
-10 |
0,72936 |
|
-12 |
0,75398 |
|
-15 |
0,81923 |
|
-18 |
0,8319 |
|
-20 |
0,8482 |
|
-22 |
0,8487 |
|
-25 |
0,8973 |
|
-28 |
0,9132 |
|
-35 |
0,9286 |
|
-40 |
0,9692 |
Из этих данных получаем численные значения коэффициентов формулы (1) при (228 К £ Т< 271,85 К) a=1,051195108 ; b= -0,00362012 ; c= 0,00386679.
При более низком диапазоне температуре (77К £ Т< 228К), получаем парамет-ры формулы (2):
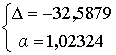
Экспериментальные данные по доли вымороженной воды
в мякоти семена граната в сопоставлении с данными других фруктов (ASHRAE 2002) показы-вает, что расчетные и
экспериментальные данные по доли вымороженной воды удовлетворительно совпадают.
В среднем погрешности апроксимации
имеют величины около 3,8%, максимум 5%, поэтому можно использовать формулу
(1,2) в целях дальнейшего прогнозирования ТФХ граната.
Расчет изобарной теплоемкости мякоти
семена плодов граната может проводиться в рамках аддитивной методики.
В диапазоне температур больше Ткр
(-1,3¸ 40оС) истинная изобарная теплоемкость граната совпадает с
эффективной изобарной теплоемкостью, и
может быть рассчитана по следующей формуле :
![]() (4)
(4)
где Св, Сс - изобарная теплоемкость воды, сухих
веществ, Дж/(кг·К);
Wв , Wс-
доля воды и сухих веществ в мякоти семена граната.
В диапазоне температур меньше Ткр (-1,3 оС) необходимо учитывать вли-яние
теплоты фазового перехода вода- лед в эффективной изобарной теплоем-кости
мякоти семена граната:
![]() ,
,
или
![]() , (5)
, (5)
где Сл - изобарная теплоемкость льда,
Дж/(кг·К);
Wл - доля льда в замороженной мякоти семена граната;
Wвн- начальная доля воды в мякоти семена граната;
L(Т) - теплота фазового
перехода вода- лед, Дж/кг.
При этом, изобарная теплоемкость сухих веществ
граната может быть аппрок-симирована какой – либо полиномиальной функцией, в
частности, опираясь на опыт В.П. Латышева [6], линейной функцией от
температуры:
Сс(Т) = А + В·Т
, (6)
где А, В – коэффициенты, определяемые
аппроксимацией данных различных исследований [8,9] методом наименьших
квадратов; A=- 5,484×102; B= 3,163.
Теплоту фазового перехода вода-лед как функцию
температуры можно опреде-лить следующим соотношением по уравнению
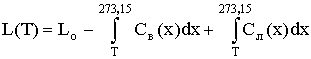 , (7)
, (7)
где Lo- теплота плавления льда при Т= 273,15 К; Lo= 333,6
кДж/кг.
Для расчета последнего интеграла в формуле (7),
используем формулу (3) и получаем следующий
результат:
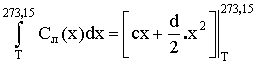 ,
(8)
,
(8)
Для расчета первого интеграла в формуле (7) его
необходимо разделить на два случая:
1) Если
228 K<
Т£ 273,15 K , то используя формулу (1), получаем:
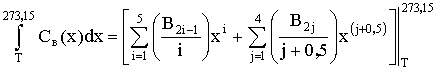 , (9)
, (9)
2) Если 77 K< Т£ 228 K , то используя обе формулы (1) и (2), получаем следующий результат:
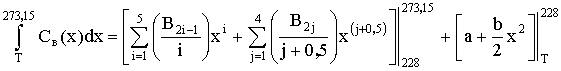 , (10)
, (10)
Поставив (8-10) в формулу (7), получаем
окончательную формулу для расчета теплоты фазового перехода вода- лед L(T).
Объединяя
формулы (2¸10), получаем модель для прогнозирования эффективной теплоемкости граната в
диапазоне температур (-196,15оС¸ 40оС).
На
основании расчетной формулы для эффективной теплоемкости граната получаем
формулу для расчета температурной зависимости энтальпии граната.
![]()
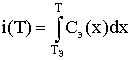 , (11)
, (11)
При этом расчет Сэ(Т) проводится по
формулам (4-5). Однако, формулу (5) можно преобразовать к виду, более удобному для интегрирования:
![]() , (12)
, (12)
Из формулы (7) вытекает, что ![]() ,тогда получаем следую-щее соотношение:
,тогда получаем следую-щее соотношение:
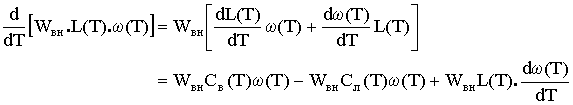 , (13)
, (13)
Поставив формулу (13) в формулу (12), получаем следующую формулу для Се
![]() , (14)
, (14)
Поставив формулу (14) в интеграл (11), получаем
формулу для расчета энтальпии:
Если Т ³ Ткр, то 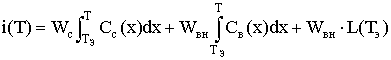 , (15)
, (15)
Если Т <
Ткр , то
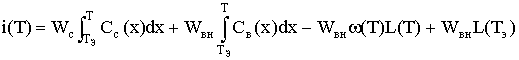 , (16)
, (16)
В итоге, на основании соотношений (1¸16) были разработаны процедуры для расчета и
прогнозирования температурных зависимостей эффективной теплоемкости и энтальпии
граната. При сопоставлении результатов расчета эффективной изобарной
теплоемкости с различными
экспериментальными данными других авторов
видно, что результаты расчетов достаточно совпада-ют с
экспериментальными данными. Погрешность между расчетными и экспе-риментальными
данными по эффективной теплоемкости оценена в пределах ±6 %. Эти результаты расчета свидетельствуют об
эффективности разработанной методики прогнозирования изобарной эффективной
теплоемкости и энтальпии мякоти семена граната.
Литература
1. Магеррамов М.А Теплофизические свойства
натуральных и концентриро-
ванных плодоовощных соков. Баку, Элм, 2006, 274 с.
2. Магеррамов М.А. Свойства плодов
граната и их хранение в модицирован-
ной атмосфере. Баку, ААСУ, 2002, 185
с.
3. Polley S.L., Shyder O.P., Kotnour P.A. Compilation
of thermal properties of
foods // J.Food Technology.-1980.-No.11.-P.78-94
4. Archer D. G. , Carter R. W. Thermodynamic Properties of the NaCl+ H2O
System.4. Heat Capacities of H2O and NaCl(aq)
in Cold-Stable andSuperco-
oled States // J. of Physic Chemical Biology(Pub. on Am. Chem. Soc. ).-2000.-
Vol.104 .-P.8563-8584.
5.
Han
B., Bischof J. C. Thermodynamic Nonequilibrium Phase Change Behavior and
Thermal Propeties of Biological Solutions for Cryobiology Applications // J.of
Biomechanical Engineering( Transactions of the ASME).-2004.-Vol.126.
-P.196-203.
6. Латышев В.П. Изобарная удельная теплоемкость, энтальпия
и доля вымо-роженной воды пищевых продуктов.- М.: Изд-во стандартов, 1989.- 92
с.
7.
ASHRAE Handbook. 2002 Refrigeration // Chapter 8.Thermal Properties
of foods.- SI Edition.-USA, Tullie Circle, N.E. Atlanta, 2002. - P.8.1-8.30.
8.
Pirunchana P., Methinee H. Prediction
of Internal Temperature in Mango Fruit during Heat Treatment// 31 st Congress
Science and Technology of Thailand.-2005.P-18-20.
9.
Rachit S., Methinee H. Effect of
Temperature on Thermal Properties of Mango cv. Nam Dok Mai Si Thong// Proc. of Conference on International Agricultural
Research for Development.- Stuttgart-Hohenheim (Germany).-2005.- P.471-478c.