Физика/8. Молекулярная физика

к.т.н., доц. Магеррамов М. А.,

Бакинский Государственный Колледж Пищевой Промышленности

Д.т.н., проф. Гореньков Э. С.

Всероссийский НИИ Консервной и Овощесушильной Промышленности

О возможности расчета термодинамических свойств плодоовощных соков на основе уравнения состояния

В данной работе рассмотрена возможность оценки величин некоторых термодинамических параметров (теплоемкость и др.) на основе уравнения состояния с использованием основным термодинамических соотношений. Методика расчета предложенная Гусейновым К.Д. [1], модифицирована нами в работах [2,3].

Для проведения расчетов было использовано уравнение вида:

, (1)

где а₀, а₁ и а₂ – являются постоянными для каждой изотермы.

Для температур Т= 280.16К эти постоянные имели следующие значения:

а₀ = 0,910707·10^{-3 ,} а₁= – 1,854436 , а₂= – 41491,1449.

С изменением температуры эти значения также меняются.

Это уравнение позволяет оценить величину изменения энтальпии, изобарной теплоемкости, а также термические величины жидких пищевых продуктов (в. т. числе гранатового сока).

Термодинамическая выражение изменения энтальпии имеет вид:

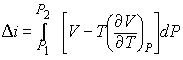(2)

Для вычисления этого интеграла надо определить величину из термического уравнения состояния (1):

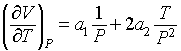(3)

Значения (1) и (3) подставим в (2) и после интегрирования в пределах от Р₁ до Р₂ получим следующее уравнение:

;

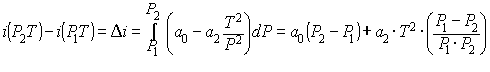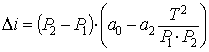(4)

Эта зависимость позволяет вычислить изменение энтальпии гранатово-го сока при различных температурах в пределах давления от Р₁ до Р_2.

Нами вычислены значения Δi при различных температурах и давлении ΔР = 10 МПа

Эти результаты представлены в таблице 1.

Таблица 1.

Значение Δ_i для гранатового сока сорта Гюлейша Азербайджанская при различных температурах и давлении Р=10 МПа

Т, К	280.16	304.18	334.19	362.19	378.17	402.18
	40.880	45.700	52.700	60.514	66.130	76.130

Графическая зависимость при является характерной кривой для жидкой фазы вещества. Согласно методике расчёта изменения энтальпии с помощью зависимости нами определено значение энтальпии для температурного шага К при Р=10 МПа.

Графический анализ функции позволил установить следующую эмпирическую зависимость:

(5)

Здесь С₀=161.280, С₁= – 4.658, С₂=0.01516.

Теперь мы можем воспользоваться следующей термодинамической зависимостью, для расчета изобарной теплоемкости (Ср) гранатового сока:

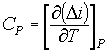(6)

Тогда производная от (5) по температуре дает для теплоемкости следующую зависимость:

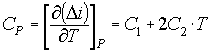, (7)

Таким образом, мы определили зависимость С_Р=φ(Т) при Р=10МПа, с помощью которой можно вычислить значение изобарной теплоемкости гранатового сока при различных температурах.

Эти данные приводятся в таблице 2.

Таблица 2.

Изобарная теплоемкость гранатового сока сорта Гюлейша Азербайджанская. при Р=10МПа

Т,К	280.16	320.16	334.16	362.16	402.18
	3.832	5.022	5.629	7.055	7.532

Полученные значения теплоемкости могут быть использованы как опорные данные для определения зависимости изобарной теплоемкости от давления; определим эффект давления на изобарную теплоемкость.

Для этой цели можно воспользоваться следующей термодинамической зависимостью:

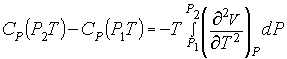, (8)

где С_р (Р₂Т) и С_р (Р₁Т) – значения теплоемкости при давлениях Р₂ и Р₁ и температуре Т. Чтобы оценить значение интеграла допустим, что при Р=const зависимость удельного объема от температуры имеет вид:

(9)

Вторая производная по Т от этой зависимости позволяет определить при Р=const:

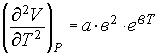(10)

Эти результаты позволяют получить из (8):

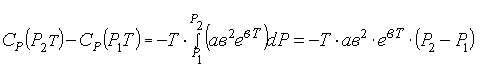(11)

Если учесть, что , тогда получим:

(12)

Значение в определяется из (11) следующим образом:

Из формулы для двух значений V и Т при Р=const получим:

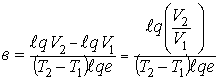(13)

Ниже приводятся результаты вычисления значения в, а также комплекса при различных давлениях (Р₁=30МПа и Р₂=50 МПа):

При Т=280.01К и в=2.3397 ּ10^-4,(1/К) получим:

Так вычисляется в и комплекс для других температур. Тогда зависимость (12) может быть записана в следующей форме:

, (14)

где значения С_Р(Р₁Т)=С_Р(10МПа,Т) приведены в таблице (2). По зависимости (14) мы определили значения изобарной теплоемкости при раз-личных температурах и давлениях. Эти результаты приводятся в таблице 3.

Таблица 3.

Изобарная теплоемкость гранатового сока сорта Гюлейша Азербайджанская.

Т, К	Давление, МПа
	10	30	50
280.16	3.382	3.500	3.269
320.16	5.022	4.695	4.459
340.16	5.629	5.280	5.021
362.16	7.055	6.682	6.405
402.18	7.532	6.906	6.806

Имея значения при 293К теплоемкости, удельного объема и коэффициента теплопроводности можно оценить величину температуропроводности a получим:

и

для температуры

Термическое уравнение состояния (1) позволяет определить также термические величины (тепловое расширение α_р и изотермическую сжимаемость β_Т:

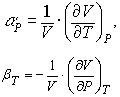(15)

Тогда величину изохорной теплоемкости можно легко определить термодинамическим соотношением:

, (16)

. (17)

По теории жидкостей и растворов предложены несколько работ. Имеется теория вязкости М.Ф.Широкова, Егера, Бриллуэна, А.М.Бачинского, Ференкеля, Панченко и др. [4,5]. Но все эти теории имеют определенные ограничения. Мы здесь рассмотрим теорию А.М.Бачинского и Френкеля. Предложенные ими расчетные уравнения для вязкости жидкости имеют теоретические основы, хотя и не описывают вязкостные свойства многих жидкостей. А.М.Бачинский экспериментально обнаружил, что между удельным объемом жидкости и ее текучестью существует линейная зависимость. Это положение нами проверялось для гранатового сока сорта Гюлейша Азербайджанская. Получена линейная зависимость. Уравнение прямой в координатах будет иметь вид:

, (18)

где , ω – собственный объем частиц жидкости, С – определенная постоянная.

На основании полученной линейной зависимости легко определяются ω и С.

Теория Френкеля более точно описывает вязкость жидкой фазы вещества, где предлагается следующая формула:

(19)

где к – постоянная Больцмана, ΔU – энергия активации частиц, А – величина постоянная. Формула (19) хорошо передает экспоненциальную зависимость вязкости от температуры. Энергии активации можно определить из формулы (19) на основании опытных значений вязкости η₁ и η₂:

(20)

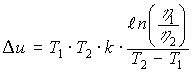(21)

Для гранатового сока можно определить значения для температур Т₂=334.16 К и Т₁=310.27 К.

При этих условиях для энергии активации сока получим следующее значение:

ΔU =1.2·10^-20Дж. (22)

Расчёт энергии активации при более высоких температурах показывает её уменьшение, что соответствует закономерностям молекулярной физики. При нагреве сока объем его увеличивается, то есть увеличивается расстояние между частицами, а также координационное число, что способствует уменьшению энергии активации.

Таким образом, предложенная нами методика расчета калорических (С_р, С_v), а также изменения термодинамических и термических величин при различных параметрах состояния может быть применена многокомпонент-ным пищевым жидкостям, каким является также гранатовый сок.

Литература

1. Гусейнов К.Д. Исследование термодинамических и переносных свойств ряда кислородсодержащих органических веществ в широком интервале параметров состояния: Автореф. Дисс… д- ра техн. наук. Баку, 1979.

2. Магеррамов М. А. Свойства плодов граната и их хранение в модифици-рованной атмосфере. Баку, ААСУ, 2002, 185 с.

3. Магеррамов М.А.Математическое описание расчетов теплофизических величин жидких пищевых продуктов // Производство и ремонт машин: Сборник материалов международной научно-технической конференции – Ставрополь: Издательство Ст. ГАУ «АГРУС», 2005. с. 191-197.

4. Панченков Г. М. Теория вязкости жидкостей, Гостехиздат. М.-Л. 1947 г.

5. Юсупов . Расчет теплоемкости хлопкового масла при повышенных параметрах температуры и давления //Хранение и переработка сельхозсырья. 1996. № 4. с. 9-11