И.А.Будько, А.Н.Волков, И.Б.Челпанов

МЕТОДЫ ЗАДАНИЯ ГЕОМЕТРИЧЕСКИХ ФОРМ ЗМЕЕПОДОБНЫХ РОБОТОВ

Сообщения об автоматических технических устройствах с более или менее сложной механикой, предназначаемых не для выполнения конкретных работ, а только для демонстрации, занимают все большее место в средствах информации, большинство их называется роботами. Понятие «демонстрационные роботы» было введено коллективом авторов, кафедры «Автоматы» СПбГТУ в серии публикаций, появившихся в последнее десятилетие в самом конце девяностых годов [1]. В настоящее время признано, что демонстрационные роботы представляют самостоятельный класс роботов со своими отличительными особенностями и типажом. К демонстрационным роботам относятся машины, подвижные или с подвижными составными частями, с автоматически управляемыми приводами, которые не выполняют никаких производственных функций, а демонстрируют или сами себя или другие объекты. Демонстрационные роботы широко используются в рекламе, для привлечения внимания на выставках, в сфере развлечений, в парках и аттракционах, на сценах театров [2], во время празднеств и шествий. Для некоторых видов демонстрационных роботов устраиваются соревнования (например, для роботов-гладиаторов, ведущих бои друг с другом). Большую популярность получили матчи колесных, управляемых вручную минироботов-футболистов. В демонстрационных роботах в первую очередь привлекает элемент изобретательства, однако многие демонстрационные роботы заслуживают серьезного научного рассмотрения, их механизмы, приводы, системы управления.

В оснащении театральной сцены, в кинематографии и на телевидении используются специально спроектированные демонстрационные роботы обычно при имитации живых существ.

В этой работе рассматриваются змеевидные или змееподобные демонстрационные роботы, роботы-змеи изменяемой геометрии, для которых характерно наличие длинного основного изгибающегося туловища. Голова может иметь самостоятельные степени свободы, но может представлять собой последнее звено туловища, у китайских драконов также имеются лапы. Известно, что змееподобный дракон является непременным участником празднеств в ряде стран юго-восточной Азии, была высказана заинтересованность в создании управляемого (на тросах) летающего дракона для Вьетнама длиной порядка 100-200 метров. Нет сомнения в том, что движущиеся змеи и драконы меньших, но достаточно больших размеров найдут место в постановках (в первую очередь со сказочными сюжетами) многих больших театров всего мира.

Конструкции демонстрационных роботов изменяемой геометрии и их составных частей могут строиться, или как многозвенные механизмы последовательной структуры с жесткими звеньями, или как деформируемые по всей длине протяженные упругие несущие элементы. Возможно также комбинирование обоих принципов.

В подавляющем большинстве случаев большие демонстрационные роботы строятся на несущих конструкциях, как на внутренних каркасах-скелетах, с легкой, декоративной наружной оболочкой, обшивкой. Если оболочка, которая формирует внешний облик, является жесткой, то ее крепление к стержневому или ферменному каркасу обычно осуществляется во многих точках, при изгибах необходимо обеспечивать подвижность, отсутствие касания смежных фрагментов или проскальзывание без заклинивания. Но не исключено, что гибкая (в частности, гофрированная) обшивка может быть использована, не только, как формирующая внешний облик, но и как несущая. В настоящее время несущие пластиковые обшивки бескаркасных конструкций используются исключительно в роботах, малых по размерам.

Объяснению и расшифровке механизмов движения змей, разработке их математических моделей и созданию подвижных макетов, в которых копируются именно такие принципы, заложенные живой природой, посвящено большое число публикаций (например, [4,5]). Признано, что сам принцип движения только за счет изгибания туловища без конечностей основан на использовании различий между коэффициентами трения в продольном и поперечном движениях.

Однако в соответствии с общей идеологией демонстрационной робототехники в данной статье речь идет о разных, возможно совершенно иных, но приспособленных для технической реализации способах построения их механизмов и воспроизведения типичных для змей геометрических форм в движении. Имеется в виду разделение задач движения на следование определенной траектории и на задание самого движения. Предполагается, что движение может задаваться колесами с приводами, которые могут быть неуправляемыми ни по скорости, ни по углам поворота.

Желаемые законы переменной геометрии и кинематики змееподобных роботов независимо от конструкций определяются следующими основными требованиями:

1. Точки средней линии сечений при извивании должны перемещаться по одной и той же неподвижной волнообразной траектории.

2. Движение в движущейся вместе со змеей системе координат представляется волной, бегущей от головы к хвосту.

3. Должны быть предусмотрены возможности изменения боковых отклонений от прямой линии в широких пределах.

4. Налагаются ограничения сверху на кривизну средней линии сечений, которые вытекают из конструктивных ограничений; при этом непрерывность кривизны не требуется.

5. Должна обеспечиваться приспособленность для программирования и воспроизведения с помощью системы приводов.

Для начала не будем учтывать естественную конструктивную дискретизацию тела змеи по длине. Важнейшим исходным моментом является выбор формы волнообразной траектории движения, бегущая волна в движущейся системе координат по этой форме должна быть использована, как программа управления автоматической системой приводов. Задание формы в виде синусоиды применительно к данной задаче представляется непригодным, явным недостатком синусоиды является непрерывное изменение кривизны и большая кривизна в вершинах при больших амплитудах.

При перечисленных требованиях может быть использована только параметрическая форма задания траектории в виде x(s) и у(s). В качестве аргумента s целесообразно выбрать длину дуги s участка траектории от выбранной начальной точки. Тогда для движения змеи со скоростью V определение координат точек его средней линии сечений по длине осуществляется непосредственно заменой аргумента s на (l + Vt – l₀).

Важно, что в программном движении вектор скорости каждой точки змеи по длине направлен по касательной к траектории. Это значительно облегчает возможности разнообразных принципиальных, схемных и конструктивных решений, а также реализации подобных движений на управляемых приводах. Например, вдоль по длине тела можно расположить опоры качения с осями, перпендикулярными средней линии сечений. Для сценического демонстрационного робота не исключена прокладка по всей длине рельсового пути, и тогда движение по нему будет происходить без проскальзывания.

Авторы предлагают формировать форму траектории в неподвижной системе координат (или бегущей волны в движущейся системе координат) сопряжением дуг окружностей радиуса R со смещенными центрами. На рис.1 изображен только один период такой волны, i-й участок длиной Δl, начинающийся от средней линии.

Рис. 1

Как форма, так и длина дуги на периоде определяется двумя параметрами: радиусом R и углом α. Аналитическое представление такой формы по половинам периода:

при 0< s <R(π +2α), т.е. для первой половины периода

x(Δs1) = R[cos α -cos (Δs1 /R –α)] ; y(Δs1) = R [sin α + sin(Δs1 /R –α)]

(1)

при R(π +2α) < s < 2R(π +2α), т.е. для второй половины периода

x(Δs2) = R[cos α -cos (Δs2/R –α)] ; y(Δs2) = -R [sin α + sin(Δs2/R –α)]

(2)

В этих выражениях приращение длины дуги Δs₁ отсчитывается от начала периода (от точки А_i), а приращение длины дуги Δs₂ отсчитывается от середины периода (от точки В_i).

При этом получаются следующие соотношения связи между длиной S₀ дуги на периоде, радиусом R, углом α, длиной дуги L по средней линии сечений, поперечным размахом В (т.е. габаритным размером) и смещением h центров круговых участков:

S0 =2R(π +2α); L= 4 R cos α; h= R sin α; В= 2 R(1 + sin α)

(3)

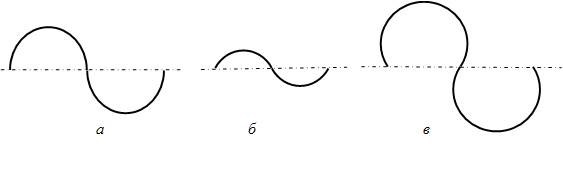
Простота этих соотношений определяет хорошую приспособленность предлагаемой формы для программирования движений. Характерные формы трех вариантов кривых при принятом аналитическом способе представления для одного и того же значения радиуса R представлена на рис.2 а, б, в. Здесь значения параметра α соответственно имеют значения α = 0, α = - 30⁰ , α = + 30⁰. Отрицательным значениям угла α соответствует более плавная и при том же значении радиуса R более короткая волна, при этом форма напоминает синусоиду.

Рис. 2

Три последовательные фазы такого движения, при котором все точки змеи перемещаются по одной и той же периодической траектории (пунктир), изображены на рис.3.

Рис. 3

Применительно к задачам управления формой важно, что при данном представлении кривизна и радиус кривизны кусочно-постоянны и изменяют знак два раза на периоде волны. Это позволяет создавать бегущую волну релейным управлением приводами по участкам.

СПИСОК ЛИТЕРАТУРЫ

1. Челпанов И.Б. Устройство промышленных роботов 2-ое изд; - СПб: Политехника, 2001.

2. Волков А.Н. Демонстрационная робототехника театральной сцены. Докторская диссертация. СПбГПУ, 2007.

3. Волков А.Н., Смородов П.В., Челпанов И.Б. Демонстрационные роботы на сцене театра: фигуры великанов в тетралогии Вагнера «Кольцо Нибелунга», Теория механизмов и машин, № 3, СПб, 2004.

4. Черноусько Ф.Л. Динамика змееподобных роботов. Материалы Всерос. Научно-техн. фестиваля. М. 2005.

5. Черноусько Ф.Л. Управление движением многозвенников на шероховатой плоскости. Труды ИММ УрО РАН, т. 6, 2000 № 1.