Карачун В.В., Мельник В.Н.
Национальный технический университет Украины «КПИ»
аКУСТИЧЕСКИЙ ИМПЕДАНС ПОПЛАВКОВОГО ПОДВЕСА
Продемонстрируем схему реализации метода Бубнова-Галеркина на уравнениях подвеса:
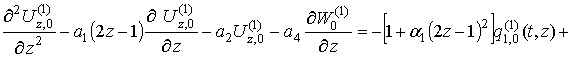
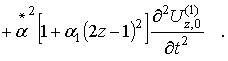 (1)
(1)
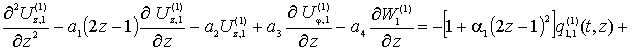
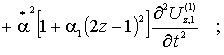 (2)
(2)
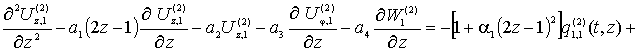
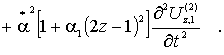 (3)
(3)
Для других уравнений все процедуры аналогичны.
Вначале
аппроксимируем отыскиваемые функции в самом общем виде:
![]()
![]() (4)
(4)
![]()
В принятых аппроксимациях использованы такие значения:
![]() (5)
(5)
- множества координатных функций
в направлении координаты z, полные и независимые в интервале (0,1).
При использовании метода
Бубнова-Галеркина, аппроксимации вида (3) предполагаются удовлетворяющими всем
(кинематическим и силовым) граничным условиям при z=0, z=1. Какой конкретный вид должны
иметь граничные условия для функций ![]() и
и ![]() на краях оболочки, т.е. при z=0 и z=1, предмет дальнейших
исследований. Вместе с тем, уже сейчас можно сказать, что концы оболочки (z=0, z=1) свободны от закреплений и это
очень усложняет проблему выбора функций (5).
на краях оболочки, т.е. при z=0 и z=1, предмет дальнейших
исследований. Вместе с тем, уже сейчас можно сказать, что концы оболочки (z=0, z=1) свободны от закреплений и это
очень усложняет проблему выбора функций (5).
Поэтому заранее в (4)
введем функции ω(z) Н.Ф.Кравчука, с помощью которых
можно удовлетворить любым граничным условиям.
Применительно к нашей
задаче, речь идет о функции типа
![]() (6)
(6)
где m,n- целые числа.
Умножим первую
аппроксимацию в (4) на ![]() вторую- на
вторую- на ![]() третью- на
третью- на ![]() где
где ![]() -
некоторые целые числа.
-
некоторые целые числа.
Таким образом,
получаем новые аппроксимации:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
где
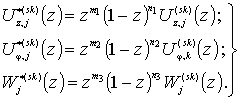 (10)
(10)
Интегрирование дифференциальных уравнений (1). Подставим в
уравнения (1) аппроксимации вида:
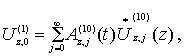 (11)
(11)
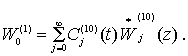 (12)
(12)
Получаем:
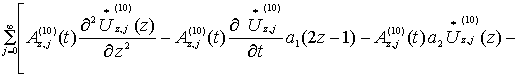 (13)
(13)
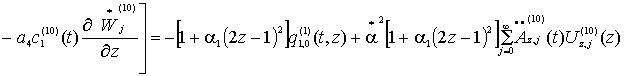 .
.
Умножим (13) на
произвольную функцию ![]() и проинтегрируем в пределах от 0 до
1. Получим систему обычных дифференциальных уравнений для определения амплитудных коэффициентов:
и проинтегрируем в пределах от 0 до
1. Получим систему обычных дифференциальных уравнений для определения амплитудных коэффициентов:
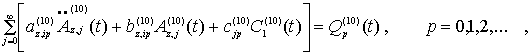 (14)
(14)
здесь
![]()
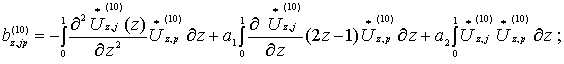
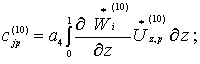 (15)
(15)
![]()
Интегрирование дифференциальных уравнений (2) и (3).
Подставим в уравнения
(2) , (3) следующие аппроксимации:
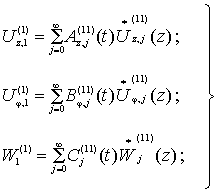 (16)
(16)
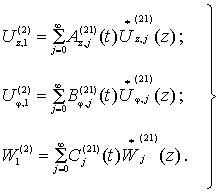 (17)
(17)
Рассмотрим уравнение (2)
и с учетом (16) вычислим
входящие в него производные:
![]() 1
1 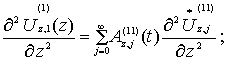
![]()
![]()
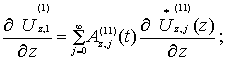
![]()
![]()
![]()
![]()
![]()
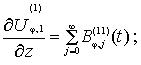 (18)
(18)
![]()
![]()
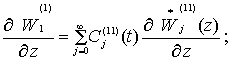
![]() 1
1 ![]()
![]() 1
1 ![]()
В
итоге получаем:
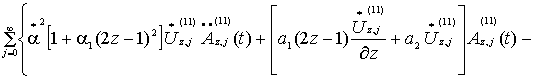
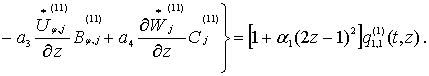 (19)
(19)
Умножим
(19) на функцию ![]() и проинтегрируем в пределах от 0 до 1 (по
координате z). Получаем
следующую систему обыкновенных дифференциальных уравнений для определения
функций
и проинтегрируем в пределах от 0 до 1 (по
координате z). Получаем
следующую систему обыкновенных дифференциальных уравнений для определения
функций ![]() ,
, ![]() ,
, ![]() :
:
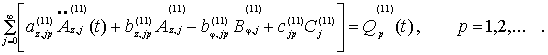 (20)
(20)
Коэффициенты
этих уравнений определяются из формул:
![]()
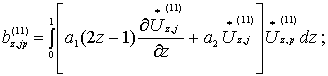
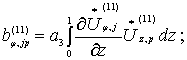 (21)
(21)
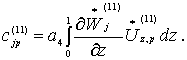
Переходим
к уравнению (3) с учетом аппроксимаций (17). Проводя аналогичные вычисления,
получаем следующую систему обыкновенных дифференциальных уравнений для
определения функций ![]()
![]()
![]()
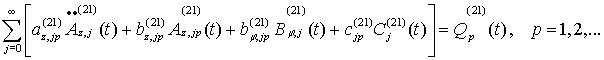 (22)
(22)
Коэффициенты
этих уравнений определяется из соотношений:
![]()
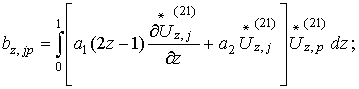
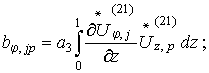 (23)
(23)
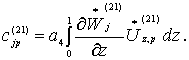
Можно получить иные системы обыкновенных дифференциальных уравнений для
определения амплитудных функций времени, которые будут входить в аппроксимации
решений дифференциальных уравнений в частных производных.