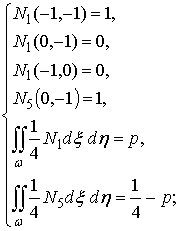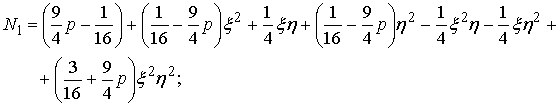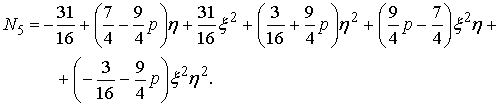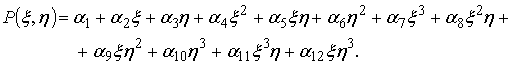Математика / 5. Математическое моделирование
Астионенко
И.А.
Херсонский
национальный технический университет, Украина
Серендиповы модели суперпараметрических аппроксимаций
Общие вопросы применения полиномиальных
аппроксимаций в методе конечных элементов (МКЭ) рассматривали многие авторы,
начиная с середины 60-х годов прошлого века. В 1968 г. Эргатудис, Айронс и
Зенкевич [1, 2] привели интересные примеры изопараметрических конечных
элементов, названных впоследствии серендиповыми конечными элементами (СКЭ).
Получены они были в результате модификации конечных элементов лагранжева
семейства путем исключения внутренних узлов.
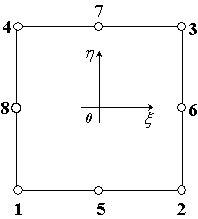
Рассмотрим биквадратичный СКЭ: это квадрат
размером 2х2, на границе которого регулярно расположены 8 узлов (рис.1).
|
|
|
|
|
Рис. 1
Биквадратичный СКЭ |
Рис. 2
Бикубический СКЭ |
Стандартный интерполяционный полином для
СКЭ-8 в общем виде имеет 8 параметров:
|
|
(1) |
где 
неопределенные
коэффициенты, которые находят методом обратной матрицы. После соответствующих
преобразований получают функции формы в явном виде [1]:
|
|
(2) |
;
|
|
(3) |
;
|
|
(4) |
;
Полученные базисные функции (функции
формы) обладают следующими свойствами (условия типа Лагранжа):
|
|
(5) |
,где 
− символ Кронекера,
− номер функции, 
− номер узла;
|
|
(6) |
.Кроме того, функции формы 
обеспечивают
непрерывность на границе: если узел 
принадлежит
конкретной стороне квадрата, то функция 
вдоль этой стороны
изменяется по закону квадратичной параболы (3 узла).
В литературе [3] изопараметрическими
принято называть элементы, у которых число узлов, определяющих форму элемента,
равно числу узлов, определяющих интерполяционную функцию. Число узлов,
используемых для определения формы элемента, может быть меньше или больше числа
узлов, используемых при определении интерполяционной функции. Такие элементы
называются субпараметрическими и суперпараметрическими соответственно.
В настоящей работе суперпараметрической
аппроксимацией будем называть такую, при которой интерполяционный полином типа
(1) имеет параметров больше, чем количество узлов в элементе. С помощью таких “внеузловых”
параметров можно избавиться от недостатков, характерных для стандартных
изопараметрических моделей, например, неестественного распределения равномерной
массовой силы по узлам (отрицательные нагрузки в угловых узлах).
Задача поиска суперпараметрического
интерполяционного полинома успешно решена несколькими способами [4-9]. В данной
работе предлагается новый метод, который позволяет получить бесчисленное
множество функций формы, зависящих от заданной переменной величины. При этом
возникает возможность, изменяя значение переменной, менять свойства
интерполяционного полинома.
Суперпараметрический полином для СКЭ-8
получим с помощью комбинированного алгебро-геометрического
подхода. Не нарушая условие изменения функции формы вдоль стороны по закону
квадратичной параболы, можно представить 
и 
в виде:
|
|
|
|
|
|
Неизвестные коэффициенты 
найдем, решив систему,
составленную с помощью (5):
|
|
(7) |
С помощью входящих в систему интегралов
вычисляют долю соответствующего узла в поузловом распределении равномерной
массовой силы. Приравнивая их переменной 
(в последнем
уравнении – зависимость 
от 
), мы получаем возможность записать функции формы 
в виде выражений, зависящих
от одной переменной 
− узлового значения равномерной массовой силы в вершине
КЭ. Решив систему (7), получим:
|
|
(8) |
|
|
(9) |
Функцию 
легко получить из 
перестановкой 
и 
. Найденные функции формы запишем в общем виде:
|
|
(10) |
;
|
|
(11) |
;
|
|
(12) |
;
Полученные базисные функции полностью
соответствуют условиям (5), (6).
Изменяя значение переменной 
, получаем бесчисленное множество базисов. Несложно увидеть,
что при 
(узловое значение
равномерной массовой силы в стандартном наборе функций формы) формулы (10)-(12)
переходят в (2)-(4). Наиболее естественным с физической точки зрения является
диапазон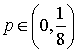 
, в котором все узловые значения положительные, а срединные –
больше угловых.
Чтобы определить, как будет выглядеть
интерполяционный полином типа (1) для этого базиса, раскроем все скобки в (8),
(9) и перегруппируем слагаемые по степеням 
и 
:
|
|
(13) |
|
|
(14) |
С помощью треугольника Паскаля легко
определить, что интерполяционный полином имеет 9 параметров (недостающие
симметричные значения находятся с помощью 
). К стандартному
полиному (1) добавился параметр 
, который исчезает при 
.
Рассмотрим бикубический элемент СКЭ-12
(рис. 2). Стандартный интерполяционный полином этого элемента имеет 12
параметров:
|
|
(15) |
Стандартные функции формы этого элемента
можно найти, например, с помощью метода обратной матрицы [1]:
|
|
(16) |
;
|
|
(17) |
;
|
|
(18) |
;
В
этой модели, кроме упомянутого ранее недостатка, присущего всем стандартным
моделям СКЭ высших порядков – “негативизм” в поузловом распределении
равномерной массовой силы (в модели (16)-(18) угловое значение 
), появляются ещё и избыточные кратные нули в узлах на
границе КЭ. Попытаемся устранить эти недостатки, введя внеузловой параметр.
Для получения 13-параметрического полинома
воспользуемся тем же комбинированным методом, что и для СКЭ-8. На стороне
СКЭ-12 равномерно расположены 4 узла, поэтому функция формы вдоль стороны
квадрата должна изменяться по закону кубической параболы. Это условие не
нарушается, если 
и 
представить в виде:
|
|
|
|
|
|
Неизвестные коэффициенты найдем, решив
систему, аналогичную (7). Полученные при этом функции формы имеют вид:
|
|
|
;
|
|
(20) |
;
|
|
(21) |
;
Проверка показывает, что условия 
, 
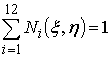выполняются. При
подстановке в (19)-(21) значения 
эти формулы переходят
в (16)-(18). Для того, чтобы выяснить, сколько параметров будет иметь
интерполяционный полином типа (15), достаточно раскрыть все скобки в 
и перегруппировать
слагаемые:
|
|
(22) |
При изменении переменной 
получаем бесчисленное
множество базисов (19)-(21), которые содержат 13-й параметр 
. При 
этот параметр
исчезает, при этом интерполяционный полином (22) становится стандартным.
Некоторые известные ранее другие модели можно получать как частные случаи при
определенных значениях 
. Модифицированная модель отличается от стандартной тем, что
количество кратных нулей в узлах уменьшилось, а также исчезают отрицательные
нагрузки в распределении равномерной массовой силы по узлам, если переменная 
. В диапазоне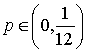 
значения поузловой
нагрузки в узлах 
превышают значения в
угловых узлах, что с физической точки зрения выглядит наиболее естественно.
Появление альтернативных базисов с
управляемыми характеристиками открывает новые возможности для решения задачи
оптимизации свойств серендиповых моделей. Представляет большой интерес поиск
для СКЭ-12 интерполяционных полиномов с
14, 15 и 16 параметрами.
ЛИТЕРАТУРА:
1. Зенкевич О. Конечные
элементы и аппроксимация / О. Зенкевич, К. Морган. ― М.: Мир, 1986.
― 318 с.
2. Ergatoudis I. Curved isoparametric “quadrilateral” elements for
finite element analysis/ I.Ergatoudis, B.M. Irons, O.C. Zienkiewicz //Internat.
J. Solids Struct., 4, 1968. ― P. 31-42.
3. Сегерлинд Л. Применение метода
конечных элементов / Л. Сегерлинд.
― М.: Мир, 1979. ― 392 с.
4. Хомченко А.Н.
Некоторые вероятностные аспекты МКЭ / А.Н. Хомченко. ― Ивано-Франк. ин-т
нефти и газа. ― Ивано-Франковск, 1982. ― 9 с. ― Деп. в ВИНИТИ
18.03.82, №1213.
5. Хомченко
А.Н. О базисных функциях МКЭ для
уравнений в частных производных / А.Н.
Хомченко // ІІІ Респ. симпозиум по диффер. и интегр. уравнениям: Тез.
докл. ― Одесса: ОГУ, 1982.
― С. 257-258.
6. Камаева Л.И. О
моделировании конечных элементов серендипова семейства / Л.И. Камаева, А.Н.
Хомченко // Прикл. проблемы прочности и пластичности: Всесоюз. межвуз. сб.
― Горький: ГГУ, 1985. ― С. 14-17.
7. Хомченко А.Н.
Геометрия серендиповых аппроксимаций / А.Н. Хомченко, Е.И. Литвиненко, П.И.
Гучек // Прикл. геом. и инж. графика. ― К.: Будівельник, 1996. ― Вып. 59. ― С.
40-42.
9. Хомченко А.Н.
Обратные задачи об интегральных средних для серендиповых полиномов / А.Н.
Хомченко, И.А. Астионенко, Е.И. Литвиненко // Вестник Херсонского национ. техн.
университета. Вып. 2(28). ― Херсон: ХНТУ, 2007. ― С. 383-389.
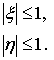