М. П. Ленюк
Чернівецький
факультет НТУ «ХПІ»
ПІДСУМОВУВАННЯ ФУНКЦІОНАЛЬНИХ РЯДІВ ЗА ВЛАСНИМИ ЕЛЕМЕНТАМИ ГІБРИДНОГО
ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА ФУР’Є – ЕЙЛЕРА – ЛЕЖАНДРА НА СЕГМЕНТІ ![]() ПОЛЯРНОЇ ОСІ
ПОЛЯРНОЇ ОСІ
Побудуємо обмежений на множині
![]()
розв’язок сепаратної системи з диференціальних рівнянь Фур’є, Ейлера та
Лежандра для модифікованих функцій
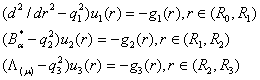 (1)
(1)
за крайовими мовами
![]() ,
,![]() (2)
(2)
та умовами спряження
![]() (3)
(3)
Умови на коефіцієнти: ![]()
![]()
![]()
У рівності (1) беруть участь диференціальні
оператори Фур’є ![]() [1], Ейлера
[1], Ейлера ![]() [1], та
Лежандра
[1], та
Лежандра ![]() [2]:
[2]: ![]()
![]() ;
; ![]() ,
, ![]() .
.
Фундаментальну систему
розв’язків для диференціального рівняння Фур’є ![]() складають функції
складають функції ![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера
[1]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера ![]() складають функції
складають функції
![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Лежандра
[1]; фундаментальну
систему розв’язків для диференціального рівняння Лежандра ![]() складають
узагальнені приєднані функції Лежандра першого роду
складають
узагальнені приєднані функції Лежандра першого роду ![]() та другого роду
та другого роду ![]() [2].
[2].
Наявність фундаментальної системи розв’язків дає
можливість побудувати розв’язок крайової задачі (1) – (3) методом функцій Коші
[1,3]: 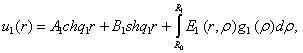
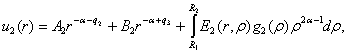
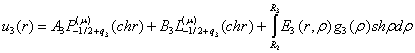 (4)
(4)
У рівностях (4) беруть участь функції Коші![]() [1,3]:
[1,3]:
![]()
![]() (5)
(5)
Тут ![]() .
.
Припустимо, що функція Коші
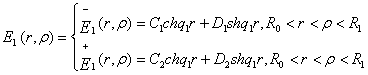
Властивість (5) для визначення
величин ![]() дають алгебраїчну
систему з двох рівнянь
дають алгебраїчну
систему з двох рівнянь
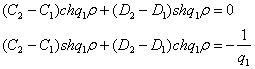
Звідси отримуємо співвідношення:
![]() (6)
(6)
Рівності (6) доповнимо
алгебраїчними рівняннями:
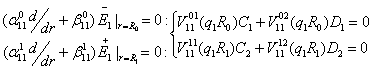 (7)
(7)
Алгебраїчна система (7) завдяки
рівностям (6) набуває вигляду:
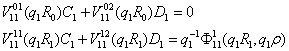
За правилами Крамера [4] знаходимо, що
![]()
Цим функція Коші ![]() визначена і внаслідок
симетрії відносно діагоналі
визначена і внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
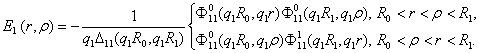 (8)
(8)
У формулах (7), (8) беруть участь функції:
![]()
![]()
![]()
![]()
Нехай функція Коші
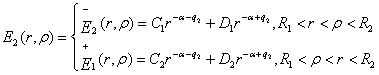
Згідно з властивостями
(5) маємо алгебраїчну систему з двох рівнянь:
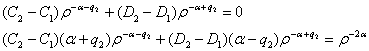
Звідси одержуємо
співвідношення:
![]() (9)
(9)
Доповнимо рівності (9)
алгебраїчними рівняннями:
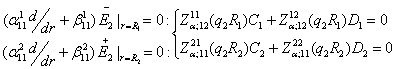 (10)
(10)
Алгебраїчна система (10) в силу
рівностей (9) набуває вигляду:
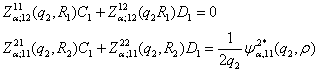 (11)
(11)
Згідно правил Крамера [4] маємо:
![]()
Цим функція Коші ![]() визначена і внаслідок
симетрії відносно діагоналі
визначена і внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
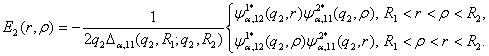 (12)
(12)
У рівностях (10), (12) беруть участь функції:
![]()
![]()
![]()
![]()
Припустимо, що функція
Коші
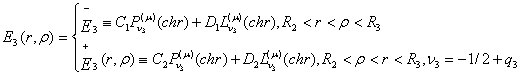
Властивості (5) функції
Коші дають алгебраїчну систему з двох рівнянь:
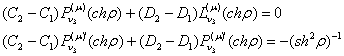
Звідси одержуємо
співвідношення:
![]() (13)
(13)
Доповнимо рівності (13)
алгебраїчними рівняннями:
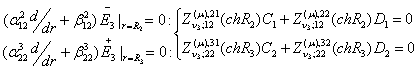 (14)
(14)
Алгебраїчна система (14)
внаслідок співвідношень (13) набуває вигляду:
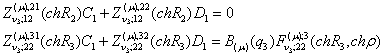
Згідно правил Крамера [4] одержуємо, що
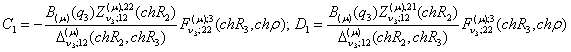
Цим функція Коші ![]() визначена і внаслідок
симетрії відносно діагоналі
визначена і внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
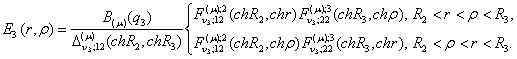 (13)
(13)
У формулах (14), (15) беруть участь функції:
![]()
![]()
![]()
![]()
![]()
![]() - гама функція
Ейлера.
- гама функція
Ейлера.
Повернемось до формул (4).
Крайові умови (2) та умови спряження (3) для визначення величин ![]() дають алгебраїчну
систему із шести рівнянь:
дають алгебраїчну
систему із шести рівнянь:
![]()
![]()
![]() (16)
(16)
![]()
У системі (16) беруть участь функції
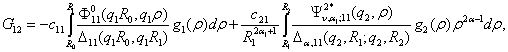 .
.
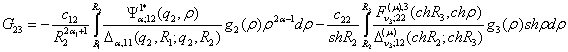
та символ Кронекера ![]() [4].
[4].
Введемо до розгляду
функції:
![]()
![]()
![]()
![]()
Припустимо, що виконана умова однозначної розв’язності даної
крайової задачі (1) - (3): для
будь-якого відмінного від нуля вектора ![]() визначник
алгебраїчної системи (16) відмінний від нуля:
визначник
алгебраїчної системи (16) відмінний від нуля:
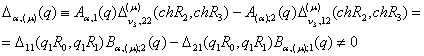 (17)
(17)
Визначимо головні розв‘язки крайової задачі (1) – (3):
1) породжені крайовою умовою в точці ![]() функції Гріна
функції Гріна
![]()
![]()
![]() (18)
(18)
2) породжені
неоднорідністю умов спряження функції Гріна
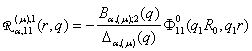 ,
, 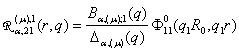 ,
,
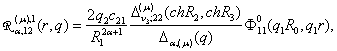
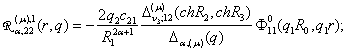 (19)
(19)
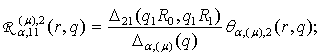
![]()
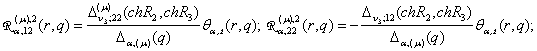
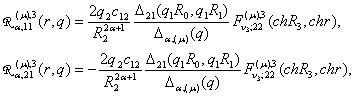
![]()
3)
породжені неоднорідністю системи функції впливу
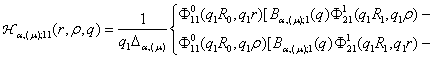
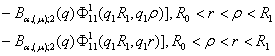 ,
,
![]()
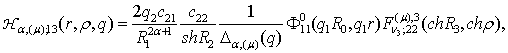
![]() (20)
(20)
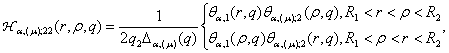
![]()
![]()
![]()
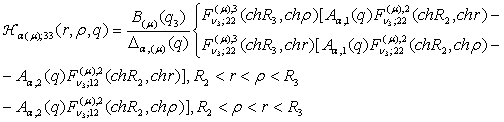
4) породжені крайовою
умовою в точці ![]() функції Гріна
функції Гріна
![]()
![]() (21)
(21)
![]()
У результаті однозначної розв’язності алгебраїчної
системи (16) й підстановки одержаних значень ![]() та
та![]() у формули (4) маємо єдиний розв’язок крайової задачі (1) –
(3):
у формули (4) маємо єдиний розв’язок крайової задачі (1) –
(3):
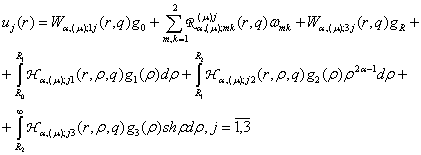 (22)
(22)
Побудуємо
розв’язок крайової задачі (1) – (3) методом інтегрального
перетворення, породженого на множині ![]() гібридним диференціальним оператором (ГДО)
гібридним диференціальним оператором (ГДО)
![]() (23)
(23)
![]() - одинична функція Гевісайда [3].
- одинична функція Гевісайда [3].
Самоспряжений ГДО не має на множині ![]() особливих точок. Тому спектр його
дискретний. Цьому спектру відповідає дискретна спектральна функція (власна
функція операторна
особливих точок. Тому спектр його
дискретний. Цьому спектру відповідає дискретна спектральна функція (власна
функція операторна ![]() ).
).
Для знаходження власних елементів ГДО ![]() (власних чисел та
відповідних їм власних функцій) розглянемо спектральну задачу Штурма –
Ліувілля: побудувати ненульовий розв’язок системи звичайних диференціальних
рівнянь Фур’є, Ейлера та Лежандра
(власних чисел та
відповідних їм власних функцій) розглянемо спектральну задачу Штурма –
Ліувілля: побудувати ненульовий розв’язок системи звичайних диференціальних
рівнянь Фур’є, Ейлера та Лежандра
![]()
![]() (24)
(24)
![]()
за однорідними крайовими умовами
![]() (25)
(25)
та однорідними умовами спряження
![]() (26)
(26)
Тут ![]() - компоненти
спектральної вектор-функції
- компоненти
спектральної вектор-функції
![]()
![]() - спектральний
параметр,
- спектральний
параметр, ![]()
Фундаментальну систему розв’язків
для диференціального рівняння Фур’є ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера
[1]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера ![]() утворюють функції
утворюють функції
![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Лежандра
[1]; фундаментальну
систему розв’язків для диференціального рівняння Лежандра ![]() утворюють функції
утворюють функції
![]() та
та ![]() [2];
[2]; ![]() .
.
Наявність фундаментальної системи розв’язків дозволяє
написати:
![]() ,
,
![]() , (27)
, (27)
![]()
Крайові умови (25) й умови спряження (26) для визначення
шести величин ![]() дають однорідну
алгебраїчну систему із шести рівнянь.
дають однорідну
алгебраїчну систему із шести рівнянь.
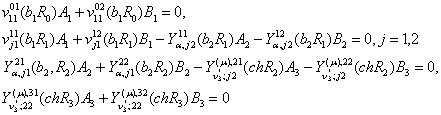 (28)
(28)
У
системі (28) беруть участь функції
![]()
![]()
![]()
![]()
![]()
![]()
Алгебраїчна
система (28) має ненульові розв’язки тоді і тільки тоді, коли визначник системи рівний нулю [4]:
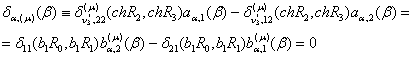 (29)
(29)
У рівності (29) прийняті
позначення:
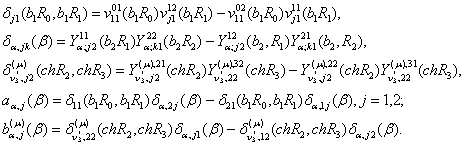
Корені ![]() трансцендентного
рівняння
трансцендентного
рівняння ![]() утворюють дискретний
спектр ГДО
утворюють дискретний
спектр ГДО ![]() [5]: дійсні, різні, симетричні
відносно
[5]: дійсні, різні, симетричні
відносно ![]() й на піввісі
й на піввісі ![]() складають монотонно
зростаючу числову послідовність з
єдиною граничною точкою
складають монотонно
зростаючу числову послідовність з
єдиною граничною точкою ![]() .
.
Підставимо в систему (28)
![]() й відкинемо останнє
рівняння в силу лінійної залежності. Покладемо
й відкинемо останнє
рівняння в силу лінійної залежності. Покладемо ![]()
![]() - підлягає визначенню.
Перше рівняння системи перетворюється в тотожність.
- підлягає визначенню.
Перше рівняння системи перетворюється в тотожність.
Розглянемо
алгебраїчну систему стосовно ![]() :
:
![]() (30)
(30)
Визначник системи (20)
![]() .
.
Алгебраїчна
система (30) має єдиний розв’язок [4]:
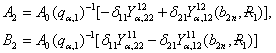 (31)
(31)
Розглянемо алгебраїчну систему
стосовно ![]() :
:
![]() (32)
(32)
Визначник
алгебраїчної системи (32)
![]()
Тут беруть участь величини:
![]()
![]()
Алгебраїчна система (32) має
єдиний розв’язок:
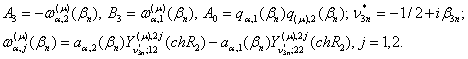 (33)
(33)
Підставимо в рівність
(27) визначені величини ![]() згідно формул (31),
(33). Отримаємо функції:
згідно формул (31),
(33). Отримаємо функції:
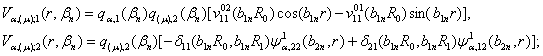 (34)
(34)
![]()
![]()
![]()
Цим спектральна (власна) функція ![]() визначена.
визначена.
Введемо до розгляду вагову функцію
![]() (35)
(35)
й квадрат норми спектральної
функції
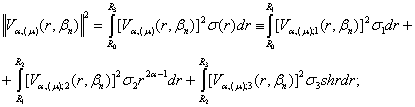 (36)
(36)
![]()
Згідно
з роботою [5]
сформулюємо твердження.
Теорема 1. (про власну функцію).
Система ![]() власних функцій ГДО
власних функцій ГДО ![]() ортогональна на
множині
ортогональна на
множині ![]() з вагою
з вагою ![]() , повна і замкнена.
, повна і замкнена.
Теорема
2. (про зображення рядом Фур’є). Будь-яка вектор-функція ![]() з області визначення
ГДО
з області визначення
ГДО ![]() зображається за
системою
зображається за
системою ![]() абсолютно й
рівномірно збіжним на
абсолютно й
рівномірно збіжним на ![]() рядом Фур’є:
рядом Фур’є:
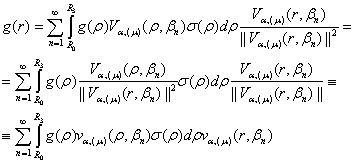 (37)
(37)
Ряд Фур’є (37) визначає пряме ![]() та обернене
та обернене ![]() скінченне гібридне інтегральне перетворення (СГІП), породжене
на множині
скінченне гібридне інтегральне перетворення (СГІП), породжене
на множині ![]() ГДО
ГДО ![]() :
:
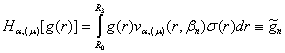 , (38)
, (38)
![]() (39)
(39)
Визначимо величини та функції
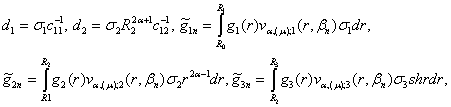
![]()
Теорема 3. (про основну тотожність). Якщо вектор-функція
![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовiльняють крайові умови (2)
та умови спряження (3) то справджуються основна тотожність СГІП ГДО
задовiльняють крайові умови (2)
та умови спряження (3) то справджуються основна тотожність СГІП ГДО ![]() :
:
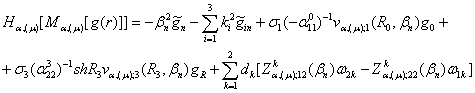 (40)
(40)
Формули (38), (39) та (40) утворюють математичний апарат, потрібний для розв’язання крайової задачі (1) – (3)
методом СГІП.
Скористаємось відомою
логічною схемою [5].
Запишемо систему (1) в матричній формі:
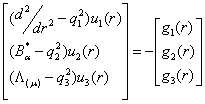 (41)
(41)
Оператор ![]() згідно правила (38)
зобразимо у вигляді операторної матриці-рядка:
згідно правила (38)
зобразимо у вигляді операторної матриці-рядка:
![]()
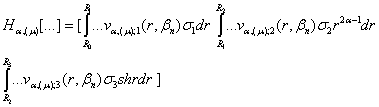 (42)
(42)
Застосуємо до системи
(41) за правилом множення матриць операторну матрицю-рядок (42). Внаслідок
тотожності (40) маємо алгебраїчне рівняння
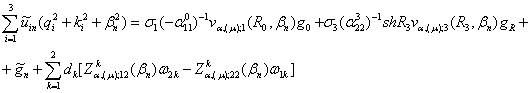 (43)
(43)
Припустимо, що ![]() . Покладемо
. Покладемо ![]() ,
, ![]() ;
;![]()
![]() .
.
Із рівняння (43) знаходимо, що
функція
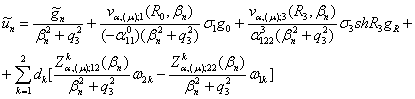 (44)
(44)
Оператор ![]() згідно правила (39)
як обернений до (42) зобразимо у вигляді операторної матриці-стовпця:
згідно правила (39)
як обернений до (42) зобразимо у вигляді операторної матриці-стовпця:
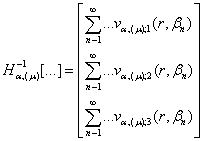 (45)
(45)
Застосувавши операторну матрицю-стовбець (45) за правилом
множення матриць до матриці-елемента ![]() , де функція
, де функція ![]() визначена формулою (44), маємо
єдиний розв’язок крайової задачі (1) – (3):
визначена формулою (44), маємо
єдиний розв’язок крайової задачі (1) – (3):
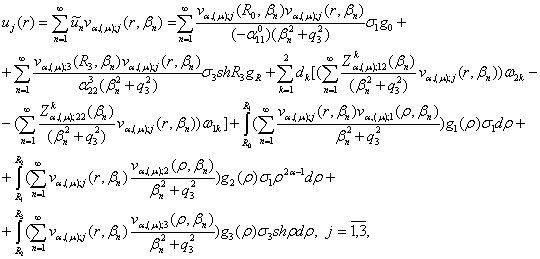 (46)
(46)
Порівнюючи розв’язки (22) та (46) в силу єдиності, приходимо до
низки формул підсумовування функціональних рядів за власними елементами ГДО ![]() :
:
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
Функції впливу ![]() визначені формулами (20), функції
Гріна
визначені формулами (20), функції
Гріна ![]() умов спряження визначені формулами
(19), функції Гріна
умов спряження визначені формулами
(19), функції Гріна ![]() визначені формулами (21).
визначені формулами (21).
Зауваження 1: Якщо ![]() , то
, то ![]()
![]() і вираз
і вираз ![]() заміниться на
заміниться на ![]() . Якщо
. Якщо ![]() то
то ![]()
![]() і замість
і замість ![]() буде всюди
буде всюди ![]() .
.
Зауваження 2: Праві частини формул (47) – (51) не залежать від
нерівностей ![]() .Тому при необхідності можна покласти
.Тому при необхідності можна покласти ![]() .
.
Висновком проведеного в роботі дослідження є твердження.
Основна теорема: Якщо вектор-функція ![]() задовільняє умови
теореми про основну тотожність і виконується умова (17) однозначної
розв’язності крайової задачі (1) – (3), то мають місце формули (47) –
(51)підсумовування поліпараметричних функціональних рядів за власними
елементами ГДО
задовільняє умови
теореми про основну тотожність і виконується умова (17) однозначної
розв’язності крайової задачі (1) – (3), то мають місце формули (47) –
(51)підсумовування поліпараметричних функціональних рядів за власними
елементами ГДО ![]() , визначеного рівністю (23).
, визначеного рівністю (23).
Література:
1. Степанов В.В. Курс дифференциальных уравнений. -
М.:Физматгиз, 1959. – 468с.
2. Конет І.М., Ленюк М.П. Інтегральні перетворення типу Мелера
– Фока. – Чернівці: Прут, 2002. – 248с.
3.
Шилов Г.Е. Математический анализ.
Второй специальный курс.- М.: Наука, 1965. – 328с.
6. Курош А.Г. Курс высшей алгебры.- М.: Наука, 1971. – 432с
7. Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні
інтегральні перетворення, породжені диференціальними рівняннями другого
порядку. – Чернівці: Прут, 2001. – 228 с.