Технические науки / 4. Транспорт
К.т.н., Айтбаев К.
АО «Казахстанский дорожный научно-исследовательский
институт», Республика Казахстан
К постановке
задачи о напряженно-деформированном состоянии
дорожной
конструкции с подземным теплопроводом
По сложившейся традиции, в больших городах теплоснабжение
осуществляется подземным способом, и теплопроводы, как правило, заложены непосредственно под проезжей частью.
Ремонт таких теплосетей сопряжены с известными затруднениями при эксплуатации
городских дорог, так как приводит
вскрытию дорожной одежды.
Автомобильные дороги, под которыми проложен
теплопровод, чаще выходят из строя из-за появления в них деформаций в виде
сквозных продольных трещин, параллельных направлению подземного теплопровода и
просадок дорожного покрытия над ним. Как известно, одна из причин этому явлению
имеет механическую природу. Наличие подземного, жесткого железобетонного
коллектора в грунтовой среде вызывает повышенную концентрацию напряжений вокруг
угловых точек железобетонного коллектора [1]. Другая, возможно наиболее
существенная, причина повышенной
податливости дорожной конструкции с подземным теплопроводом может заключаться в
особенностях температурного поля, формируемого вокруг подземного теплопровода.
Появление зон, в которых температура не
опускается ниже нулевой отметки в течение всего года, может изменить
влажностный режим грунта под дорожной одеждой, что, в конечном счете, приведет
к ослаблению основания, подстилающего дорожную одежду.
Построение математической модели многослойной дорожной
конструкции с подземным теплопроводом предполагает полноты информации о
теплофизических и физико-механических
свойствах слагающих частей рассматриваемой конструкции. Однако, для
упрощения процесса выявления напряженно-деформированного состояния дорожной
конструкции, ограничимся учетом лишь упругих деформаций.
Теплопровод представляет собой пару стальных труб,
заключенных в железобетонные коллекторы прямоугольного поперечного сечения. По
одной из труб подается горячая вода потребителю, которая, после использования,
возвращается по другой трубе в центр теплоснабжения.
Для построения механической модели важны лишь деформационные
характеристики спаренных железобетонных коллекторов, поэтому будем пренебрегать
наличием в них труб водовода (рисунок 1).
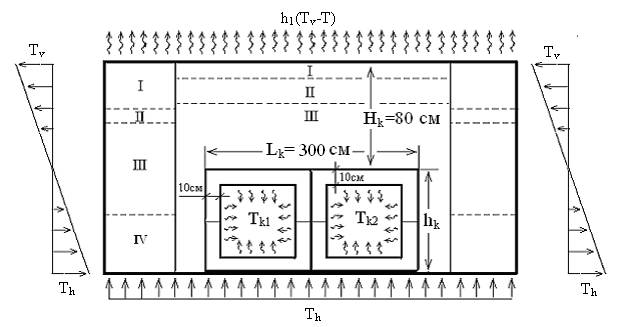
Рисунок
1. Условные обозначения: I – двухслойный асфальтобетон, II –
щебень из твердых пород, III –
гравийно-песчаная смесь, IV – грунт
естественного залегания, суглинок легкий, Tv –
температура наружного воздуха, Th –
температура грунта на глубине h м, Tk1 и Tk2 –
температура воздуха внутри коллекторов.
Определение напряженно-деформированного состояния
предполагает решения неоднородного дифференциального уравнения второго порядка
в частных производных совместно с граничными условиями. Однако, для такой
сложной области, каковой является многослойная дорожная конструкция с
подземными пустотами, получение аналитического решения представляет собой
сложную математическую задачу.
Наиболее приемлемым путем является численное решение
задачи. Для этого нужно построить функционал, определяемый полем перемещений в исследуемой области. Функция
перемещений, предоставляющая минимум данному функционалу и есть решение
вышеупомянутого дифференциального уравнения. Минимизация функционала на искомом
решении будет осуществляться методом конечных элементов.
В работе [2] приводится алгоритм
решения задачи по определению напряженно-деформированного состояния в сплошном
теле. Согласно этому алгоритму в качестве
функционала берется полная потенциальная энергия деформации, накапливаемая
сплошным телом к моменту наступления стационарного состояния процесса
деформирования.
Полная потенциальная энергия деформации вычисляется по
формуле:
![]() , (1)
, (1)
где ![]() - энергия деформации,
а
- энергия деформации,
а ![]() - работавнешних сил [2].
- работавнешних сил [2].
После
разбиения исследуемой области на конечные элементы выражение (1) запишется так:
![]() ,
,
где ![]() - полная
потенциальная энергия
- полная
потенциальная энергия ![]() -го элемента.
-го элемента.
Энергия деформации бесконечно
малого обьема ![]() тела вычисляется по
формуле [3]
тела вычисляется по
формуле [3]
![]() .
.
Здесь ![]() - полная деформация;
- полная деформация; ![]() - начальная
деформация. Величина
- начальная
деформация. Величина ![]() называется
плотностью энергии деформации. Полная энергия деформации тела определяется
путем интегрирования этой величины по всему обьему тела:
называется
плотностью энергии деформации. Полная энергия деформации тела определяется
путем интегрирования этой величины по всему обьему тела:
![]() . (2)
. (2)
Вид векторных величин ![]() и
и ![]() определяется типом
рассматриваемой задачи. Например, для двухмерной задачи
определяется типом
рассматриваемой задачи. Например, для двухмерной задачи
![]()
и
![]() .
.
В
методе конечных элементов закон Гука в общем случае запишется так:
![]() . (3)
. (3)
Здесь матрица ![]() определяется упругими
характеристиками материалов тела. А
соотношения, связывающие деформаций с перемещениями:
определяется упругими
характеристиками материалов тела. А
соотношения, связывающие деформаций с перемещениями:
![]() ,
, ![]() ,
, ![]() ,
,
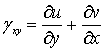 ,
, 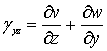 ,
, ![]() .
(4)
.
(4)
определяются через значения узловых перемещений
следующим образом:
![]() , (5)
, (5)
где ![]() -так называемая функция формы [2],
определяемая координатами узлов конечного элемента и зависящая от текущих
координат точки. Здесь
-так называемая функция формы [2],
определяемая координатами узлов конечного элемента и зависящая от текущих
координат точки. Здесь ![]() и
и ![]() компоненты перемещения
точки в направлении координатных осей
компоненты перемещения
точки в направлении координатных осей ![]() и
и ![]() .
.
Выразим
вектор деформации ![]() через перемещения
узлов
через перемещения
узлов ![]() с помощью соотношений
(4):
с помощью соотношений
(4):
![]() . (6)
. (6)
Здесь матрица ![]() определяется путем дифференцирования матрицы
определяется путем дифференцирования матрицы ![]() согласно соотношениям
(3).
согласно соотношениям
(3).
Энергия
деформации отдельного элемента ![]() будет
вычисляться с помощью формул (2) и (6):
будет
вычисляться с помощью формул (2) и (6):
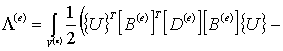
![]() . (7)
. (7)
Но, последние два слагаемых в
полученном выражении не будут учитываться при применении формулы (7), так как в
задаче не будет рассматриваться начальная деформация.
Работу
внешних сил можно разделить на три части: работа сосредоточенных сил ![]() , работа компонентов напряжений, действующих на внешних
поверхностях исследуемой области
, работа компонентов напряжений, действующих на внешних
поверхностях исследуемой области ![]() , и работа обьемных сил
, и работа обьемных сил ![]() .
.
В рассматриваемой
задаче, вектор внешних сил, согласно вышеупомянутому алгоритму [2] будет
вычисляться по формуле:
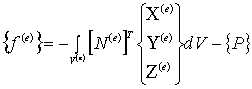 , (8)
, (8)
где первая слагаемая соответстувует весу треугольных конечных элементов, а вторая – сосредоточенным
силам, действующим в узловых точках.
Тогда полная потенциальная энергия рассматриваемого сплошного тела будет
вычисляться по формуле:
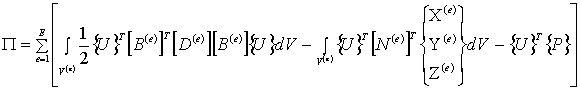 . (9)
. (9)
Для минимизации полной
потенциальной энергии нужно дифференцировать выражение (8) по ![]() , и результат приравнять нулю:
, и результат приравнять нулю:
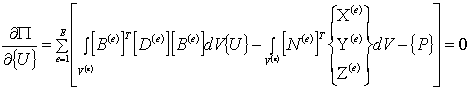 . (10)
. (10)
Интегралы в последнем выражении
определяют вектор нагрузки ![]() и матрицу жесткости
и матрицу жесткости ![]() элемента.
элемента.
В таком случае, выражение (9)
сокращенно можно записать в виде:
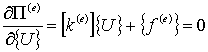 . (11)
. (11)
Здесь матрица жесткости
элемента ![]() вычисляется с помощью
следующего обьемного интеграла:
вычисляется с помощью
следующего обьемного интеграла:
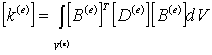 , (12)
, (12)
а вектор узловой нагрузки элемента ![]() – по формуле (8).
– по формуле (8).
Матрица
упругости в матрице жесткости (11) для случае плоского напряженного состояния
будет вычисляться по формуле:
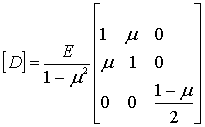 , (13)
, (13)
где ![]() модуль упругости, а
модуль упругости, а ![]() коэффициент Пуассона
материала элемента.
коэффициент Пуассона
материала элемента.
Если
условие минимума полной потенциальной энергии системы записать в матричной
форме, то получим систему линейных алгебраических уравнений равновесия,
записанную через обобщенную матрицу жесткости ![]() и вектор-столбец
и вектор-столбец ![]() узловых нагрузок:
узловых нагрузок:
![]() . (14)
. (14)
Здесь
![]() (15)
(15)
и
![]() . (16)
. (16)
Литература
1. Айтбаев К.А., Устойчивость грунтов вокруг комплекса
городских коммуникационных сооружений. Диссертация на соискание ученой степени
кандидата технических наук. Алматы: КазАТК и ИММаш МНВО РК,1999. - 133 с.
2. Сегерлинд Л. Применение метода конечных элементов. М:
Мир, 1979. – 392 с.