УДК 519.6(07)

В.П. Житников, Н.М. Шерыхалина, С.С. Поречный

Уфимский государственный авиационный технический университет

УСТРАНЕНИЕ НЕКОРРЕКТНОСТИ ПРИ ПРАКТИЧЕСКОЙ ОЦЕНКЕ ПОГРЕШНОСТЕЙ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ

Предлагается видоизмененная методика фильтрации результатов решения задач численными методами, включающая формальное правило (корректную задачу) выбора эталона, играющего роль уточненного результата вычислений. Показано, что применение предложенного правила позволяет избежать неопределенности и устранить недостатки правил Рунге и Ромберга.

Ключевые слова: оценка погрешностей, сравнение с эталоном, численная фильтрация.

Введение

Несмотря на интенсивное применение численных методов для моделирования и проектирования различных систем, а также наличие большого количества математических программных пакетов, проблема оценки вычислительных погрешностей стоит очень остро. В известных учебниках и монографиях по численным методам внимание в большей степени уделяется анализу остаточных членов, что для практики представляет большие трудности и поэтому используется редко. Очень малое внимание уделяется оценке погрешностей, связанных с округлением чисел. В связи с этим разработка надежных методов оценки погрешности численных методов весьма актуальна.

1. Математическая модель процесса оценки погрешности

Зависимость приближенных результатов вычисления многими численными методами можно представить в виде математической модели

, (1)

где z – точное значение; z_n – приближенный результат, полученный при числе узловых точек, равном n; f₁,…, f_L – некоторые функции числа узлов.

Для разностных формул численного дифференцирования, квадратурных формул Ньютона-Котеса, разностных методов решения задач для уравнений математической физики и многих других формул и численных методов , k_j – произвольные действительные числа. Некоторым другим численным методам, например, методу простых итераций соответствуют функции .

В могут входить не вошедшие в сумму слагаемые степенного вида, остаточный член, погрешность округления и многие другие составляющие, обусловленные как численным методом, так и конкретной программной реализацией. Поэтому не стремится к нулю при увеличении n, а может даже возрастать.

Пусть имеется конечная последовательность вычисленных результатов. Тогда можно записать систему линейных алгебраических уравнений

,

,

……………………………………………………… (2)

.

Если считать неизвестными искомыми параметрами наряду с z, c₁,…c_L, то неизвестных в системе (2) всегда больше, чем уравнений, и она имеет бесконечное множество решений, среди которых точное. Применяя методы регуляризации [1-5] можно получить оценку этого точного решения z и оценку погрешности. Однако известные методы регуляризации требуют задания некоторой априорной информации не только о неизвестных , но и об искомых z, c_j. Результаты такой оценки зависят от этой априорной информации, поэтому могут привести к получению ошибочных оценок.

2. Известные методы оценки погрешности

Возможен другой известный подход [6]. Рассмотрим линейную комбинацию

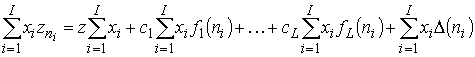. (3)

Наложим условия полного подавления компонент погрешности

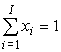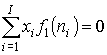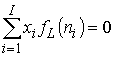, ,…,. (4)

Если I=L+1 и система функций линейно независима, то система (4) имеет единственное решение. Отметим, что эта задача имеет точное, независимое от погрешностей решение. В результате из (3) получается значение

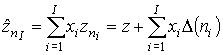, (5)

которое принимается в качестве приближенной оценки точного значения z. Это значение называют квадратурной формулой Ромберга [6]. Однако оценку погрешности этого значения найти невозможно, в связи с отсутствием априорной информации о .

Пусть , , то есть мы устанавливаем некоторый регулярный способ задания n (чаще всего величина Q выбирается равной 2). Для этого случая при решение системы (4) может быть получено путем последовательного применения экстраполяционной формулы Ричардсона [6].

Результатом этого на каждом шаге экстраполяции является треугольная матрица экстраполированных значений вида

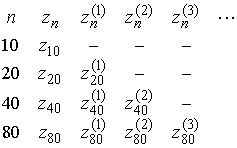(6)

Оценка погрешности проводится по правилу Рунге, т.е.

, , , … (7)

Этот процесс построения матрицы экстраполированных по Ричардсону значений (6) по строкам и сравнение (для получения оценки погрешности по правилу Рунге) двух последних элементов последней строки называют методом Ромберга.

Недостатком этого метода является отсутствие обоснованности полученных оценок в связи с неопределенностью , поскольку оценки (7) представляют собой частные случаи (5).

Этот процесс можно усовершенствовать.

Численной фильтрацией [7, 8, 9] называется последовательное устранение (подавление) компонент погрешности, т.е. определение отфильтрованных последовательностей , l=1,…,L. Для уравнений (2) фильтрация сводится к линейной комбинации , причем и определяются из решения системы двух уравнений

, .

Отсюда получаем формулу фильтрации

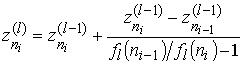. (8)

Как правило, рассматриваются случаи, когда I>L+1, тогда уравнений в системе (4) больше, чем неизвестных и матрица, аналогичная (6), не является треугольной. Матрица заполняется по столбцам с помощью формулы (8) или других фильтров [8], при этом для оценки погрешности сравнивается каждая пара значений . Для наглядности это можно проиллюстрировать на графике в логарифмическом масштабе (рис. 1), где представлены результаты обработки данных, полученных при вычислении второй разностной производной [6].

При этом шаг сетки h=1/n. По оси ординат отложены десятичные логарифмы относительных разностей , , по оси абсцисс – десятичные логарифмы n. Разности значений двух столбцов при этом представляются системой точек, которую можно условно соединить между собой некоторой кривой или ломаной. Каждая кривая близка к отрезку прямой, если слагаемые в сумме (1) существенно отличаются по величине. Угловой коэффициент каждого отрезка при () приближенно равен соответствующему показателю k_j.

На графике располагаются несколько линий, тем самым, появляется возможность сравнить их взаимное расположение. Это дает возможность заметить несоответствия, неправильность поведения линий.

Например, на рис. 1, а каждая линия имеет два четко выделенных участка. Первый участок имеет наклон, соответствующий показателю степенной функции. Поведение второго участка линий, в отличие от первого, носит хаотический характер, угловой коэффициент приближенно равен -2. Это связано с преобладанием составляющей погрешности D(n), аналогично задаче, рассмотренной в [7]. При этом применение экстраполяции Ричардсона неправомерно, так как она возможна только при преобладании составляющей, имеющий вид степенной функции с определенным показателем.

В диапазоне, где преобладает нерегулярная погрешность, меняющая знак, в качестве оценки погрешности можно использовать разность пар значений. В экстраполяционной формуле Ричардсона эта разность делится на достаточно большое число . Поэтому разница приближенного и экстраполированного результатов оказывается малой и оценка по Рунге дает завышенные по точности результаты. С этим связан сдвиг вверх (при увеличении количества фильтраций) участков линий, соответствующих условию преобладания нерегулярной погрешности. Сравнивая рис. 1, а и рис. 1, б нетрудно заметить, что оценка по Рунге соответствует реальной погрешности в диапазоне, отделенном хотя бы половиной масштабной единицы от уровня нерегулярной погрешности у=19-2×lg n.

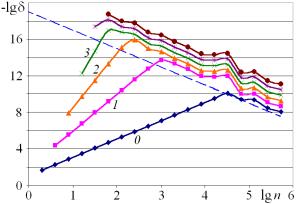
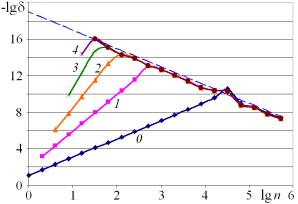
а б

Рис. 1. Оценки погрешности при вычислении второй производной: а – по правилу Рунге; б – сравнение с точным значением. Прямая у=19-2×lg n

3. Сравнение с эталоном

В отличие от правила Рунге все приближенные значения можно сравнивать с одним числом – эталоном , которое считается наиболее точным. Разность представляет собой оценку погрешности приближенного значения . В этом случае результат расчета с оценкой погрешности представляется в виде интервала .

На рис. 2 представлены результаты сравнения с эталоном при оценке погрешностей вычисления второй разностной производной. На рис. 2, а эталон выбран предложенным ниже способом. На рис. 2, б эталон искусственно загрублен в 13-м разряде. Как видно из рис. 2, б, при неправильном выборе эталона возникает характерная картина, связанная с ограничением точности на уровне, соответствующем погрешности выбора эталона.

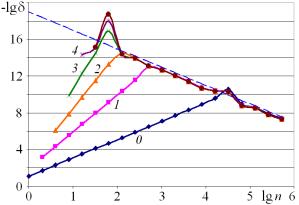
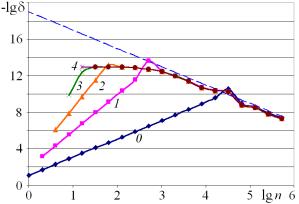
а б

Рис. 2. Сравнение с эталоном при вычислении второй производной при различном выборе эталона: а – по результатам оценки с исключением искомого; б – эталон искусственно загрублен в 13-м разряде

4. Правило выбора эталона

При выборе эталона приходится решать некорректную задачу, поскольку каждое уравнение (2) содержит неизвестное искомое z и неизвестную погрешность, состоящую из нескольких компонент.

Для уменьшения неопределенности предлагается разделить этапы оценки погрешности и определения эталона. Для этого на первом этапе проводится фильтрация по формуле

, (11)

устраняющая из последовательности неизвестное искомое z. Тем самым, дальнейшая фильтрация по формуле (8) служит оценкой погрешностей, независимой от выбора эталона (рис. 3, а).

Такая оценка лишена указанного выше недостатка правила Рунге («кажущегося уточнения»), вызванного зависимостью оценки от конкретной закономерности изменения погрешности, и субъективности, связанной «экспертным» выбором эталона.

Отметим, что преобразование (11) изменяет компоненты зависимости (1)

,

однако при это изменение незначительно. Именно этим объясняется «привязка» результата фильтрации (11) к .

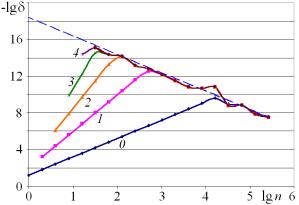
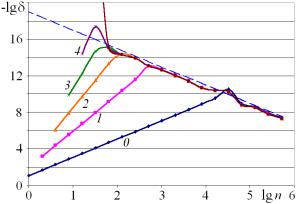
а б

Рис. 3. Результаты двухэтапной оценки погрешности с исключением искомого по формуле (11): а – оценка погрешности; б – сравнение с эталоном

Полученная таким способом оценка позволяет выбрать наилучшие, с точки зрения минимума погрешности (или комбинации близких по погрешности значений), соотношения и j=j₀. Тем самым, мы приходим к задаче минимизации

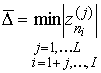, (12)

или в более общем случае при некотором постоянном k=0,1,2,…

,

,

. (13)

Значения и j=j₀, которые получаются при решении задачи минимизации, используются для определения значения (эталона, см. рис. 3 б) путем фильтрации последовательности по формуле (8).

Тем самым, определена формальная процедура (корректная задача) определения эталона . В совокупности с оценкой (13) определяется некоторое множество – интервал неопределенности.

Следует отметить, что выбор эталона на основе минимума погрешности, найденного по одному значению (12) может привести к ошибке, так как нерегулярная составляющая погрешности не исключает наличия близких по значению пар. Использование нескольких условий (13) позволяет избежать таких ошибок, хотя и несколько осложняет процедуру.

Таким образом, методика решения некорректной задачи оценки погрешности заключается в:

· фильтрации по формуле (11) и многократной фильтрации на основе формулы (8);

· выборе результата фильтрации, обладающего наилучшей оценкой погрешности;

· определении эталона согласно полученным данным путем многократной фильтрации по формуле (8) без применения формулы (11);

· оценке погрешности эталона и размытости оценки.

Выводы

Оценка погрешности вычислений является некорректной задачей. Математическая модель погрешности может быть рассмотрена как априорная информация при решении этой задачи. Адекватность этой модели проверяется результатами использования предложенной методики.

Сравнение результатов вычислений и фильтрации с единым эталоном позволяет, в отличие от правила Рунге, получать оценки погрешности в условиях преобладания нерегулярной составляющей погрешности D(n).

Предложенное правило исключения искомого дает возможность выбрать эталон с наименьшей в условиях данного эксперимента погрешностью.

СПИСОК ЛИТЕРАТУРЫ

1. Морозов В. А. Регулярные методы решения некорректно поставленных задач. − М.: Наука, 1987. − 240 с.

2. Тихонов А. Н., Гончарский А. В., Степанов В. В. и др. Численные методы решения некорректных задач. − М.: Наука, 1990. − 290 с.

3. Тихонов А. Н., Леонов А. С., Ягола А. Г. Нелинейные некорректные задачи. − М.: Наука, 1995. − 312 с.

4. Федотов А. М. Некорректные задачи со случайными ошибками в данных. − Новосибирск: Наука, 1990. − 280 с.

5. Зверев Г. Н., Дембицкий С. И. Оценка эффективности геофизических исследований скважин. − М.: Недра, 1982. − 224 с.

6. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. - М.: Наука, 2004. – 636 с.

7. Житников В. П., Шерыхалина Н. М., Поречный С. С. Об одном подходе к практической оценке погрешностей численных результатов. Научно-технические ведомости СПбГПУ. Информатика. Телекоммуникации. Управление. 3(80)/ 2009, СПб, 2009. С. 105–110.

8. Шерыхалина Н. М. Методы обработки результатов численного эксперимента для увеличения их точности и надежности // Вестник УГАТУ (сер. Управление, вычислительная техника и информатика), 2007. Т. 9, №2 (20). – С. 127-137.

9. Житников В. П., Шерыхалина Н. М. Обоснование методов фильтрации результатов численного эксперимента // Вестник УГАТУ, 2007. Т. 9, №3. – С. 71-79.