УДК 517.98

д.ф.-м.н., проф. Фетисов В.Г., Панина И.И.

Южно-Российский государственный университет экономики и сервиса, г. Шахты, Россия

МОДИФИКАЦИЯ ТОПОЛОГИЧЕСКОГО ПРИНЦИПА КРАСНОСЕЛЬСКОГО ДЛЯ С-НОРМИРОВАННЫХ ПРОСТРАНСТВ

Известны различные варианты классической теоремы Банаха о сжатых отображениях. В настоящей работе доказано обобщение топологического принципа Красносельского-Дарбо для суммы итерированного оператора сжатия и вполне непрерывного, действующей в с-нормированных пространствах.

ОПРЕДЕЛЕНИЕ 1. (cм. также [1]) Пусть X – линейное пространство. Функционал , называется обобщенной нормой или с-нормой, если выполняются условия:

1) 0≤ g(u)<+, для любого элемента ;

2) при и , где – нуль линейного пространства Х;

3) если , то , где a, b – любые действительные числа и элемент ;

4) для любых , где выбор с не зависит от элементов ;

5) для любого , .

Само исходное пространство X называется обобщенным нормированным пространством.

Аналогичным образом вводится определение обобщенного метрического пространства и рассматриваются предельные соотношения, понятия сходимости и другие сведения, с ними связанные.

Пусть даны две обобщенные нормы (метрики) и , определенные на X. Обозначим через , если из условия при следует условие при , где . Если и , то будем говорить, что обобщенные нормы и эквивалентны.

Сначала приведем ряд конструктивных примеров обобщенных с-нормированных (метрических) пространств, играющих роль среды рассматриваемой нелинейной динамической системы.

ПРИМЕР 1. Если g(u) – c-норма, то функция , где – любое положительное число, также является c-нормой.

Аналогичное утверждение справедливо и для обобщенных метрик.

ⁿ

ПРИМЕР 2. Пусть М(u) и N(v) – взаимно дополнительные друг к другу по Юнгу N-функции. Через G обозначим замкнутое ограниченное множество n-мерного евклидова пространства , а через – класс таких измеримых по Лебегу, определенных на G функций u(x), для которых конечен интегральный модуляр вида

.

Обозначим через класс всех таких измеримых функций u(x), для которых

для любой функции .

Функция тогда и только тогда, когда

для любой функции , для которой .

Как известно, если , то

.

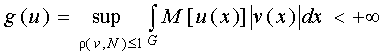Если M(u) удовлетворяет -условию [2], то функция g(u) является с-нормой на , причем пространство полно относительно с-нормы g(u).

ПРИМЕР 3. Пусть S –пространство всех измеримых на G функций. Функция

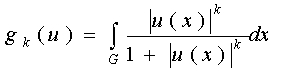
является с-нормой на S, причем пространство S является полным, где . Можно заметить, что все с-нормы g_k(u), k=1,2,…, эквивалентны между собой, а сходимость по с-норме эквивалентна сходимости по мере.

ПРИМЕР 4. Пусть является -функцией (см. [3]); и – две взаимно дополнительные N-функции по Юнгу. Рассмотрим интегральный модуляр вида:

,

а через обозначим класс функций :

.

В классе можно задать с-норму по формуле Люксембурга:

.

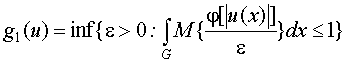Аналогично в классе можно ввести и другую с-норму по формуле Орлича:

,

причем с-нормы и эквивалентны.

ПРИМЕР 5. Пусть . Положим

.

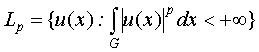Определим с-норму в следующим образом:

.

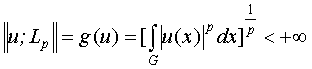Как показал Кёте 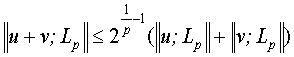, то есть является с-нормированным пространством, причем (см. [4]).

Из приведенных примеров видно, что постоянная с может принимать различные положительные значения. В связи с этим представляет определенный интерес следующее замечание.

Для любого числа в любом с-нормированном пространстве X можно ввести такую эквивалентную с-норму, что с=а.

Красносельским в [5] был получен известный топологический метод неподвижной точки, который представляет собой линейную комбинацию принципа сжатых отображений Банаха и принципа неподвижной точки Шаудера. Учитывая итерационные соображения, докажем следующую теорему:

ТЕОРЕМА 1. Пусть А – линейный оператор в с-нормированном полном пространстве X, n-я итерация которого является оператором сжатия, а оператор В, заданный на ограниченном замкнутом выпуклом множестве , вполне непрерывен, причем для любых элементов . Тогда уравнение имеет по крайней мере одно решение .

◄ Пусть задан любой фиксированный элемент . Так как по условию теоремы n-я итерация оператора А есть оператор сжатия, то , значит, уравнение

(1)

имеет единственное решение , причем согласно условию настоящей теоремы это решение принадлежит исходному множеству D. Можно заметить, что решение является однозначной функцией от , так как исходный оператор А является линейным.

Подставляя в уравнение (1), получим справедливое при каждом элементе тождество

, (2)

Очевидно, что оператор K отображает множество D в себя.

Сначала предположим, что однозначный оператор K является вполне непрерывным. В силу принципа Шаудера оператор будет иметь по крайней мере одну неподвижную точку, принадлежащую множеству , то есть для некоторого элемента .

Учитывая тождество (2), получим, что , то есть утверждение теоремы имеет место в случае полной непрерывности оператора K. Обоснование факта полной непрерывности оператора K вытекает из следующей цепочки рассуждений.

Используя линейный оператор А в обеих частях формулы (2), получим следующее тождество:

(3)

Аналогично, применяя теперь оператор А к обеим частям предыдущего тождества (3) и учитывая (2), имеем:

(4)

Продолжая процесс образования новых аналогичных тождеств, получим при каждом n>1

(5)

Меняя в последней формуле u на v, имеем:

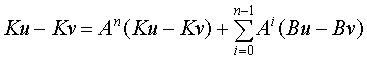. (6)

Учитывая, что , можно видеть, что для любых элементов , будет справедливо неравенство вида:

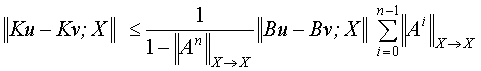. (7)

А так как исходный оператор В по условию настоящей теоремы вполне непрерывен, то из последней мажорантной оценки (7) для вспомогательного оператора K непосредственно вытекает полная непрерывность оператора K.►

Библиографический список.

1. Леви, П. Конкретные проблемы функционального анализа [Текст] : монография / П. Леви. – М.: Наука, 1967. – 474 c.

2. Красносельский, М.А. Выпуклые функции и пространства Орлича [Текст] : монография / М.А. Красносельский, Я.Б. Рутицкий. – М.: Физматлит, 1958. – 272 с.

3. Фетисов, В.Г. Операторы и уравнения в линейных топологических пространствах [Текст] : монография / В.Г. Фетисов, В.И. Филиппенко, В.Н. Козоброд ; под общ. ред. В.В. Обуховского. – Владикавказ: ВНЦ РАН, 2006. – 432 с.

4. Przeworska-Rolewicz, D. Equations in linear spaces / D. Przeworska-Rolewicz, S. Rolewicz. – Warszawa, 1968. – 380 p.

5. Красносельский, М.А Топологические методы в теории нелинейных интегральных уравнений [Текст] : монография / М.А. Красносельский. – М.: ГИТТЛ, 1956. – 392 с.