к.ф.-м.н. А.И. Долгарев

Структура галилеева пространства-времени

Структура пространства-времени общей теории относительности существенно отличатся от структуры пространства-времени специальной теории относительности. Указанным пространствам соответствуют некоммутативное галилеево пространство и классическое пространство-время Галилея. Ниже рассматриваются основные понятия галилеевых пространств и проводится аналогия с пространствами из теории А. Эйнштейна.

Существует аналогия между структурами пространства-времени в теории относительности А.Эйнштейна и пространства-времени Г. Галилея. Это закономерно, так как пространство-время Галилея является предельным случаем пространства-времени в теории Эйнштейна. Переход от системы отсчета, в которой событие имеет координаты к системе отсчета, где то же событие имеет координаты в теории Эйнштейна осуществляется в результате преобразований Лоренца

, , , ;

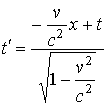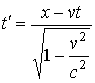а в пространстве-времени Галилея в результате преобразований Галилея:

, , , .

Если скорость события мала по сравнению со скоростью света , т.е. стремится к нулю, то формулы Лоренца превращаются в формулы Галилея.

1. О структуре пространства-времени в теории относительности.

Структура пространства-времени специальной теории относительности (СТО) принципиально отличается от структуры пространства-времени в общей теории относительности (ОТО), см., например, [1, с. 615 – 639], в популярном изложении: [1, с. 37 – 38]. В указанных книгах вопрос о пространстве-времени Галилея не обсуждается.

Временные (времени-подобные) мировые линии наблюдателей в пространстве-времени в СТО являются прямыми линиями. К ним перпендикулярна 3-мерная пространственная (пространственно-подобная) составляющая пространства-времени. Здесь может идти речь о слоении пространства-времени в СТО.

В случае ОТО конгруэнции мировых линий наблюдателей искривлены. Направление движения наблюдателя задано касательной к мировой линии наблюдателя. В ОТО каждый наблюдатель в каждый момент времени определяет 3-мерное пространственное направление ортогонально касательной к мировой линии наблюдателя. Указанные пространственные направления возможно не сшиваются в гладкое пространство. О слоении говорить не проходится.

В пространстве-времени в СТО можно ввести глобальную систему отсчета, в пространстве ОТО – только локальную. Пространство-время в ОТО настолько искривлено, что множество одновременных событий не составляет евклидовой гиперплоскости. Однако, некоторую аналогию с галилеевыми некоммутативными пространствами можно усмотреть.

2. Пространство-время Галилея и его евклидовы гиперплоскости.

Имеется линейное и коммутативное классическое пространство-время Галилея и некоммутативные галилеевы пространства.

Пусть есть линейное пространство действительного аффинного пространства , и , , векторы из . Операции над векторами:

, , ,

поле действительных чисел. В вводится галилеево скалярное произведение векторов

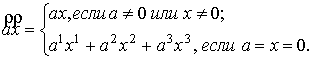(1)

Линейное пространство с галилеевым скалярным произведением векторов называется галилеевым векторным пространством и обозначается .

Для вектора определяется галилеева норма равенством

, (2)

в координатах имеется:

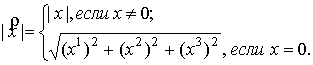(3)

Галилеева норма векторов относится к квазинормам в виду того, что галилеево скалярное произведение векторов определяется двумя равенствами.

Первая компонента вектора называется временной, остальные компоненты вектора называются пространственными. В связи с этим изменяются обозначения компонент векторов:

.

Векторы , согласно определению (3) галилеевой нормы, являются евклидовыми; векторы , , называются галилеевыми векторами. Евклидовы векторы составляют в 3-мерное евклидово подпространство, это евклидово подпространство наибольшей размерности в пространстве . Векторы и называются перпендикулярными, если . Выполняется:

Лемма. Всякий галилеев вектор перпендикулярен всякому евклидову вектору. #

В результате введения галилеева скалярного произведения векторов в линейное пространство аффинного пространства , аффинное пространство становится пространством-временем Галилея и обозначается . Точка аффинного пространства называется еще событием пространства . Событие происходит в момент времени и имеет пространственные координаты . Множество всех событий есть мир . Траектория движения события называется мировой линией события . Прямые линии аффинного пространства являются прямыми линиями пространства-времени . Всякая прямая однозначно определяется точкой , через которую она проходит, и вектором , в направлении которого она проходит:

;

она является мировой линией события . Прямая есть множество точек:

. (4)

Зафиксируем момент времени . Множество событий есть множество одновременных между собой событий.

Утверждение 1. Множество событий , одновременных с событием , является евклидовой гиперплоскостью в пространстве-времени Галилея , ее векторное пространство есть – 3-мерное евклидово подпространство галилеева пространства .

# Пусть и два события из . Парам событий соответствуют векторы

в , векторы евклидовы, и все эти векторы составляют евклидово векторное подпространство пространства . Следовательно, множество событий является в евклидовой гиперплоскостью с векторным пространством . #

Утверждение 2. Пусть лежит в евклидовой гиперплоскости , , , – галилеевы векторы. Тогда галилеевы прямые перпендикулярны гиперплоскости и параллельны между собою.

# Векторы и перпендикулярны, так как по (1), скалярное произведение , см. лемму. Все векторы параллельны временной оси , начало отсчета, . В коммутативном пространстве имеется один вид параллельных прямых. #

3. Некоммутативное галилеево пространство-время с растраном.

Линейное пространство над является коммутативным одулем Ли. К некоммутативным одулям Ли относится растран , заданный на многообразии следующими операциями:

, ; (5)

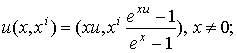
, . (6)

Элементы растрана называются растами и обозначаются малыми греческими буквами. Нулевой раст есть ; раст, противоположный расту , равен = = ; см. [3, с. 107]. Растран некоммутативная алгебраическая структура с внешней операцией, обобщает линейное пространство и относится к одулям Ли, [3, с. 102 – 115]. Одули и одулярные пространства определены в [4].

Галилеево скалярное произведение растов определяется также, как галилеево скалярное произведение векторов (1). Пусть . Имеем:

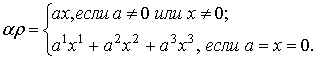(7)

Формально определения (1) и (7) совпадают. Галилеева норма раста определяется равенством:

,

ср. с (2), и вычисляется следующим образом:

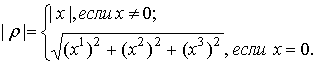(8)

Определение квазинормы растов выглядит также, как определение квазинормы векторов (3). Компонента раста называется временной, остальные компоненты называются пространственными. Раст = является вектором, все расты составляют 3-мерное евклидово векторное пространство – евклидов подрастран растрана ; операции (5), (6) при превращаются в операции над векторами. Расты , , называются галилеевыми. Всякий галилеев раст перпендикулярен всякому евклидову расту, так как (скалярное произведение этих растов равно нулю).

Рассматривается многообразие и отображение

,

в котором паре кортежей и ставится в соответствие раст

. (9)

Для отображения выполняются аксиомы Г.Вейля аффинного пространства, в которых линейное пространство заменено растраном, [3, с. 128]. Тем самым, на многообразии определено галилеево пространство время с растраном, обозначаемое . Геометрия галилеева пространства с растраном некоммутативна.

Элементы пространства называются и точками и событиями, есть некоммутативный мир. Всякое событие имеет временную компоненту и пространственные компоненты . Зафиксировав момент времени , имеем в множество событий , одновременных с событием .

Утверждение 3. Множество одновременных событий из является евклидовой гиперплоскостью галилеева пространства-времени с растраном , векторное пространство гиперплоскости есть – евклидов подрастран растрана .

# Паре событий и из соответствует раст, согласно (9),

.

Эти расты являются векторами, как уже отмечалось, см. (8), и составляют 3-мерное евклидово векторное пространство . #

Прямую галилеева пространства определим по аналогии с прямой аффинного пространства (4):

= .

При использовании операций над растами (5), (6), в [2, с. 136] получены параметрические уравнения прямой:

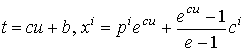, . (10)

В случае галилеева раста прямая описывается нелинейными (экспоненциальными) уравнениями, другими словами, прямые некоммутативного галилеева пространства , не лежащие в евклидовой гиперплоскости , искривлены.

Утверждение 4. Прямые , проходящие через точки евклидовой гиперплоскости в направлении галилеева раста , перпендикулярны евклидовой гиперплоскости и параллельны между собой.

# Так как евклидов раст, см. утверждение 3, и галилеев раст, то . Прямые, имеющие один и тот раст, параллельны. #

В пространстве-времени имеется два вида параллельных прямых. Во-первых, это прямые с общим растом. Во-вторых, расты и неперестановочны, поэтому раст отличен от раста и прямые не имеют общих точек, [3, с. 136]. Однако, достаточно рассматривать прямые , параллельные в одном смысле.

4. Движение во времени наблюдателей в галилеевых пространствах.

Пусть в момент времени во всех точках пространства-времени Галилея и в некоммутативном пространстве-времени с растраном находятся наблюдатели. С изменением времени наблюдатели движутся по временным мировым линиям. Система отсчета каждого наблюдателя имеет своим началом событие . Мировые линии наблюдателей являются прямыми линиями в каждом из пространств и . Структура каждого из этих пространств описывается на основании разделов 2 и 3.

Теорема 1. Мировые линии наблюдателей в пространстве параллельны; события, соответствующие положению наблюдателей в любой фиксированный момент времени, составляют 3-мерную евклидову гиперплоскость, перпендикулярную прямолинейным мировым линиям. Пространство-время плоское.

# По утверждению 1, множества событий, одновременных между собой, составляют 3-мерную евклидову гиперплоскость . Временные мировые линии, т.е. прямые, проходящие в направлении галилеевых векторов, перпендикулярны гиперплоскости в любой момент времени , утверждение 2. Как прямые линии аффинного пространства, прямые пространства-времени не искривлены, пространство плоское. #

Теорема 2. Мировые линии наблюдателей в некоммутативном галилеевом пространстве-времени , являясь прямыми в , описываются нелинейными уравнениями (10), и пэтому искривлены. В любой момент времени положения наблюдателей составляют 3-мерную евклидову гиперплоскость некоммутативного галилеева пространства-времени . Мировые линии наблюдателей перпендикулярны всякой 3-мерной евклидовой гиперплоскости галилеева пространства-времени .

# По утверждению 3, положения наблюдателей в галилеевом пространстве-времени составляют 3-мерную евклидову гиперплоскость в . Временные мировые линии, определенные галилеевыми растами, перпендикулярны всем евклидовым растам плоскости , утверждение 4, а поэтому и перпендикулярны гиперплоскости . Мировые линии (10) наблюдателей искривлены и параллельны между собою. #

Таким образом, как в пространстве-времени Эйнштейна, коммутативное и линейное 4-мерное пространство-время Галилея обладает прямолинейными мировыми линиями наблюдателей, эти прямые параллельны между собою, время наблюдателей согласовано. 3-мерные пространственные направления пространства Галилея перпендикулярны временным направлениям и составляют в каждый момент времени гладкое евклидово пространство. В этом случае пространство плоское.

В каждом некоммутативном галилеевом пространстве-времени временные мировые линии наблюдателей описываются нелинейными уравнениями. В галилеевом пространстве-времени они играют роль прямых и их галилеевы кривизны равны нулю. Но по своей сути эти мировые линии искривлены (по сравнению с коммутативным пространством). В фиксированный момент времени 3-мерные пространственные составляющие галилеева пространства-времени представляют собой 3-мерное евклидово пространство. Некоммутативное галилеево пространство-время не плоское, оно искривлено, [5].

Имеется некая аналогия коммутативного пространства-времени Галилея и пространства СТО; а также аналогия некоммутативного галилеева пространства-времени и пространства ОТО.

Структура пространства-времени в ОТО описывается локально, а структура галилеева пространства-времени описыватся глобально. Искривление некоммутативного пространства-времени обеспечивается его некоммутативностью.

В других 4-мерных некоммутативных галилеевых пространствах множества одновременных событий составляют 3-мерные евклидовы подпространства , см. [3]. Временные мировые линии событий являются прямыми, описываются нелинейными уравнениями. В пространстве с сибсоном:

, , , ;

в пространстве с диссоном:

, ,

, .

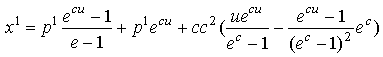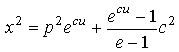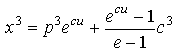Каждое из некоммутативных галилеевых пространств, изучаемых в [3], искривлено [5]. В пространствах с растраном и диссоном мировые линии наблюдателей экспоненциальны; в пространстве с сибсоном – параболы второго порядка. Римановы и псевдоримановы пространства некоммутативны. Это следует из того, что при параллельном перенесении вектора вдоль некоторого замкнутого пути , в результате получается вектор , отличный от вектора , [1, с. 411 – 515].

Псевдоевклидову пространству соответствует коммутативное пространство-время Галилея, а псевдориманову пространству соответствует некоммутативное одулярное галилеево пространство-время.

Литература

1. Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967. – 664 с.

2. Владимиров Ю.С. Пространство-время: явные и скрытые размерности. Изд.2 – М.: Книжный дом «ЛИБРОКОМ», 2010. – 208с.

3. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005. – 306с.

4. Сабинин Л.В. Одули как новый подход к геометрии со связностью //ДАН СССР. 1977. N5. C. 800 – 803.

5. Долгарев А.И. 2-параметрические кривизна и кручение 3-мерных галилеевых одулярных разрешимых пространств. – Известия высших учебных заведений. Поволжский регион. Физико-математически науки, Пенза, 2007, № 4, С. 3 – 17.