Економічні науки/8. Математичні методи в економіці

К.ф.-м.н. Мельник О.О.

ДВНЗ "КНЕУ імені Вадима Гетьмана", Україна\

Представлення поверхонь функції комплексної змінної, що інтерпретує закон Парето

В даний час економічний аналіз використовується на всіх підприємствах, які прагнуть зробити свою роботу ефективною. Одними з найбільш розвинених методів економічного аналізу є економіко-математичні методи, чия інструментальна база в основному розвивається по шляху вдосконалення існуючих методів і моделей. Нові напрями розвитку інструментальної бази економічного аналізу з'являються достатньо рідко. Одним з таких напрямів виступає теорія функцій комплексних змінних [1], яка широко використовується в природничонаукових дисциплінах, але мало використовується в гуманітарних науках, у тому числі і в економіці. Тому актуальним є питання розширення інструментальної бази економічного аналізу за допомогою економіко-математичного моделювання за рахунок використання елементів теорії функцій комплексних змінних.

Особливий інтерес представляє закон Парето. Число осіб, котрі мають прибуток не менш як , можна визначити за формулою: Лінії, які задані рівняннями називаються лініями гіперболічного типу.

Розглянемо функцію комплексної змінної вигляду закону Парето:

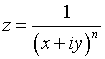. (1)

На рис.1 представлені поверхні дійсної частини [1] функції (1) при різних значеннях n.

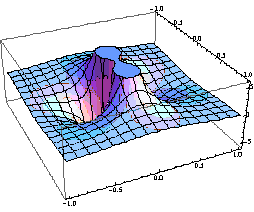
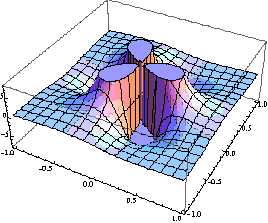
а) б)

Рис. 1. Поверхня функції 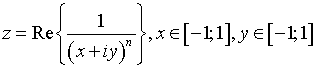при значеннях n: а) n=2; б) n =3.

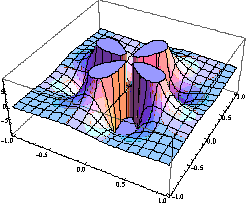
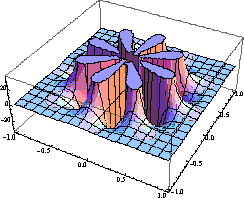
На рис.2 представлені поверхні уявної частини [1] функції (1) при різних значеннях n.

а) б)

Рис. 2. Поверхня функції 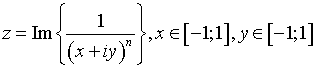при значеннях n: а) n=4; б) n =8.

Закон Парето достатньо точно описує розподіл великих прибутків, але не справджується для малих. У 1897 р. італійський економіст Вільфредо Парето вивів формулу, яка описує розподіл багатств в світі. 80/20 - 80% багатств у світі розподілені між 20% населення. Далі стали помічати, що ця формула діє в багатьох областях, наприклад, 80% населення планети живе на 20% землі. Ця формула, закон Парето, говорить приблизно про наступне: вісімдесят відсотків результату виходить з двадцяти відсотків використовуваних дій. Стосовно, скажімо, мережевого бізнесу, це означає, що всього лише двадцять відсотків вибраних вами завдань або дій, на які ви витрачаєте свій час, створять вісімдесят відсотків потрібних вам результатів.

В економіці криві обернених функцій застосовуються при вивченні взаємозв’язку між рівнем інфляції та рівнем безробіття (крива Філіпса), при аналізі уподобань споживача (крива байдужості), при вивченні факторів виробництва, які можуть бути використані для певного обсягу продукції (ізокванта), для вивчення закону розподілу прибутків (закон Парето), ринків збуту, для розв’язку задачі про розподіл зон економічного впливу.

Можна зробити висновки, що представлення основних економічних функцій у вигляді функцій комплексного змінного можливе і необхідне, що розкриває нові можливості економіко-математичного моделювання економічних процесів та систем [3].

При побудові поверхонь використовувався пакет програм Математика 8 [2], що представляє ряд нових функцій: масштабування, 2D і 3D графіки та гістограми, нові можливості для застосування текстур на поверхні і регіонів, поліпшення дискретних ділянок.

Література:

1. Блудова Т.В., Мартиненко В.С. Теорія функцій комплексного змінного. – К. Просвіта, 2000.-472 с.

2. http://www.wolfram.com/mathematica/

3. Светуньков С.Г., Светуньков И.С. Производственные функции комплексных переменных: Экономико-математическое моделирование производственной динамики. – М.: Изд-во ЛКИ, 2008. -136 с.