ДОСЛІДЖЕННЯ ДОХІДНОСТІ ЦІННИХ ПАПЕРІВ З РІВНЕМ РИЗИКУ

Лаптєва В.В.

Інвестиційний портфель являє собою єдину сукупність фінансових активів. Всі можливі комбінації інвестиційних портфелів можна представити у площині «очікувана прибутковість - середньоквадратичне відхилення». Ці комбінації інвестиційних портфелів утворюють множину допустимих портфелів. Верхня межа множини допустимих портфелів носить назву ефективна межа (efficient frontier). Портфелі, які знаходяться на ефективному кордоні (ефективні портфелі), являють собою комбінації з максимальною дохідністю при заданому рівні ризику. Увігнутість ефективного кордону пояснюється тим, що характеристики портфеля – очікувана дохідність і ризик – змінюються нелінійно по відношенню до зміни ваги активів в портфелі.

Згідно з принципом µ - σ задачу знаходження ефективного інвестиційного портфеля із n фінансових активів можна записати наступним чином:

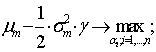(1)

при додаткових обмежених на активи інвестиційного портфеля:

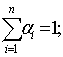
де - доходність портфеля ризикових активів; - дисперсія портфеля ризикових активів; - параметр, що відображає схильність інвестора до ризику, .

Доходність портфеля і дисперсія є функціями від ваги портфеля ,

;

,

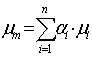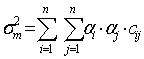де - коваріації випадкових величин доходностей активів, що входять у портфель.

Очевидно, що значення (коваріація активу з самим собою) представляють собою дисперсії -го активу . Вирішуючи завдання квадратичної оптимізації методом Лагранжа, отримуємо вираз для параметра:

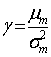, (2)

Принцип µ - σ є наслідком принципу максимізації очікуваної корисності, тому параметр задачі Марковіца повинен збігатися з постійною абсолютною мірою Ерроу-Пратта. Параметр має розмірність зворотний розмірності прибутковості, а абсолютна міра Ерроу-Пратта має розмірність, обернену розмірності багатства.

Таким чином, в моделі Марковіца абсолютна міра Ерроу-Пратта виражається через відношення прибутковості портфеля ризикових активів до його дисперсії.

Вибір персоналізованого інвестиційного портфеля в рамках портфельної теорії полягає у виборі оптимального інвестиційного портфеля з безлічі ефективних інвестиційних портфелів у відповідності з принципом µ - σ. Для врахування індивідуальних переваг інвестора при виборі оптимального інвестиційного портфеля використовують мікроекономічний апарат кривих байдужості (indifference curves). Криві байдужості – це криві, які будуються в площині «прибутковість-середньоквадратичне відхилення» (або «прибутковість - ризик») і відображають ставлення особи, що приймає рішення до ризику та дохідності. Можна припустити, що кожній особі, яка приймає рішення відповідає сімейство кривих байдужості, що відображають його переваги в термінах прибутковість – ризик. Кожної кривої байдужості відповідає певне фіксоване значення корисності, яке не змінюється при переході від однієї її точки до іншої.

У площині «очікувана прибутковість» - «ризик» інвестора, несхильності до ризику, характеризується сімейство кривих байдужості, які мають негативний нахил, інвестора - ризикофіла - сімейство кривих байдужості, що мають негативний нахил, для нейтрального до ризику інвестора криві байдужості – горизонтальні прямі. Оптимальний портфель буде розташовуватися на кривій байдужості, яка знаходиться вище і лівіше інших. Цей портфель буде відповідати точці, в якій крива байдужості стосується ефективної множини. Якщо кореляційна матриця не вироджена, то межа ефективної множини графічно відображається як вігнута функція. Тому, враховуючи, що криві байдужості інвестора, несхильного до ризику, мають негативний нахил, існує тільки одна точка дотику кривої байдужості і ефективної кордону. Інакше кажучи, існує тільки один оптимальний портфель, що задовольняє ризиковим перевагам конкретного інвестора.

Наступним кроком у розвитку портфельної теорії стала модель Дж. Тобіна, який розвинув підхід Г. Марковіца, додавши в модель безризиковий актив з доходністю і дисперсією, яка дорівнює нулю. З появою без-ризикового активу інвестор отримав можливість вкладати частину своїх грошових коштів у цей актив, а решту – в будь-який із ризикових портфе-лів, що містяться в безлічі Марковіца.

З урахуванням безризикового активу умови задачі Марковіца змінюються наступним чином:

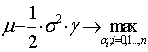(3)

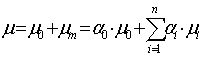
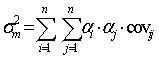
де – частка вкладень в безризиковий актив;

– абсолютна міра Ерроу-Пратта;

при додаткових обмеженнях на ваги інвестиційного портфеля:

;

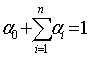; (4)

Вирішуючи завдання квадратичної оптимізації методом Лагранжа, отримуємо:

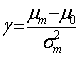. (5)

Таким чином, абсолютна міра Ерроу-Пратта в моделі Тобіна виражається через відношення різниці доходностей ризикового портфеля і без-ризикового активу до дисперсії ризикового активу. Основним недоліком подібного способу вибору оптимального інвестиційного портфеля з ефективної множини є його опора на апарат кривих байдужості, який має описовий характер в тому випадку, коли ризикові переваги особи, що приймає рішення, вже відомі.