дтн, професор Матов О.Я., ктн, доцент Василенко В. С.,

Національний авіаційний університет (НАУ), Україна

Несиметричне кодування з використанням лишкових класів. Блукання точок по числовим кільцям

Відомо, що сенсом криптографічних перетворень є така зміна початкового повідомлення (тесту, частини мовної конструкції тощо), при якій це повідомлення стає незрозумілим для тих, хто не володіє ключем зворотного перетворення, а пошук зворотного перетворення з тих чи інших причин є неприйнятним (наприклад, із-за занадто великих витрат часу - великої криптографічної стійкості). Існує багато способів таких перетворень із різною криптографічною стійкістю. Найвідомішими із таких перетворень є переклад на іншу мову (ключі перетворення - словники мов та діалектів); кодування в межах однієї із мов (наприклад, із застосуванням підміни понять, різних символів (алфавітів) для запису звуків, слів, речень тощо, коли ключами перетворення можуть бути, наприклад, кодувальні таблиці); перемішування символів з їх одночасною зміною, наприклад, із застосуванням матричних кодових перетворень та т. ін. Можливим є також комбінація із різних способів перетворення, наприклад, перехід на іншу мову (інший алфавіт) із застосуванням матричних кодових перетворень [1, 2].

Одним із найсучасніших напрямків у задачах асиметричного шифрування є шифрування на еліптичних кривих – наборах точок, обумовлених двома координатами, які є рішеннями певних рівнянь [3]. Операції в цьому рівнянні виконуються в деякому кінцевому полі, наприклад, полі лишків, по якому-небудь модулю p. Для цих точок визначається операція “додавання”, що задовольняє властивостям комутативності й асоціативності. У таких нечислових конструкціях вдається визначити задачу логарифмування так, щоб знання секрету дозволяє реалізувати швидкий алгоритм. Зокрема, цей підхід використається в прийнятому недавно російському стандарті асиметричного шифрування.

В еліптичних кривих виразилася загальна тенденція розвитку криптографічних алгоритмів з відкритим ключем: відмова від задач роботи із числовими об’єктами і перехід до більше складних й менш вивчених математичним конструкцій, благо для них сформульовано досить багато складних задач. Втім, нечислові конструкції вивчені слабко, а, отже, немає гарантії того, що через якийсь час не з’явиться ефективний алгоритм, що зробить такий шифр ненадійним.

Крім еліптичних кривих є ще кілька перспективних нечислових конструкцій, які можна використати для криптографічних цілей. Одна з них – коди, що виправляють помилки [3]. Придумані вони були для цілей зменшення втрат інформації при її передачі або зберіганні, але алгоритми відновлення виявилися настільки складними, що їх можна використати й для криптографічних цілей. Суть технології стійких до помилок кодів полягає в пошуку найближчого кодового слова в багатомірному просторі базових векторів. Виявляється, ця задача має експонентну складність, оскільки для пошуку найближчого кодового слова потрібно обчислити відстані до усіх слів. У цій статті здійснена спроба показати можливість використання підходів, відомих із галузі теорії лишкових класів, до задач побудови алгоритмів криптографічного перетворення з несиметричними ключами із застосуванням елементів нечислових конструкціях типу цифрових кіл, що дотикаються.

Прикладом застосування теорії кодів, що виправляють помилки, для криптографічних перетворень є завадостійкі криптографічні перетворення із симетричними ключами і переводом з однієї системи числення (мови запису числових послідовностей) в іншу. В [4, 5] розглянуто варіант криптографічного матричного перетворення шляхом переходу із позиційної системи числення (ПСЧ) у систему лишкових класів (СЛК), коли ключами перетворення є набір основ чи інші константи системи числення.

Зрозуміло, що можливим повинен бути й варіант криптографічного перетворення шляхом переводу зі СЛК у позиційну. З цією метою достатньо розбити вихідний (призначений для шифрування) код позиційної системи числення, наприклад, двійкової, на певні групи розрядів і вважати кожну із таких груп двійковим відображенням символу деякої системи лишкових класів. У зв’язку із тим, що таке представлення є несправжнім, умовним, будемо називати таку СЛК системою умовних лишків (СУЛ).

Звернемо увагу на те, що при обмеженому діапазоні числення (обмеженій розрядній сітці), незалежно від системи числення, що розглядається, існує максимальне число, яке можна записати в цій системі. Таке число (див. рис. 1) дорівнює (Р- 1) незалежно від системи числення (наприклад, у ПСЧ , де q- основа системи числення; в СЛК , - і - та основа СЛК, n- кількість символів (розрядів) в представленні чисел в даній системі числення). Величина Р досить часто має назву “робочого” чи “правильного” діапазону представлення, а розряди, які утворюють цей “робочий” діапазон - розрядами робочого діапазону, чи просто робочими.

Рисунок 1 - Традиційне представлення системи числення у вигляді числової вісі

При спробі збільшувати числа в таких система числення наступними знову стають числа 0, 1, 2, і т.д. Тобто будь-яка система числення при обмеженій розрядній сітці графічно може бути представлена не числовою віссю, як це робиться найчастіше (див. рис. 1, 2), а числовим кільцем (в термінах кінцевих полів), як це наведено на рис. 3, з початком відліку в точці 0 (Р).

Рисунок 2 - Перенос числа на числовій вісі із робочого діапазону у випадковий

Звернемо увагу на те, що числові кільця, залежно від величини діапазону представлення Р, тобто залежно від величини основ та їх кількості (величини розрядної сітки) мають різний розмір. При цьому сукупність числових кіл усіх систем числення для будь-яких значень основ системи числення, їх кількості чи довжин розрядних сіток має одну спільну точку дотику (рис. 3) як раз у точці початку відліку 0 (Р).

При будь-якій модифікації (спотворенні) інформації, яка відображена в робочих розрядах, модифіковане число завжди буде розташованим у межах усе того ж робочого діапазону. Тому для вирішення питань із виявлення та виправлення спотворень (модифікацій природного чи штучного характеру), в представлення чисел потрібно ввести певну надлишковість. Ця надлишковість вводиться за рахунок того чи іншого розширення розрядної сітки шляхом введення додаткових груп розрядів (чи основ). Між інформаційним змістом робочих та надлишкових розрядів установлюється певна відповідність. При цьому правила (алгоритм) вибору кількості та порядку розташування надлишкових розрядів та встановлення відповідності між інформацією робочих та надлишкових розрядів складають сутність кодування, яке по традиції прийнято називати завадостійким, а власне сукупність визначених, таким чином, змістовностей інформаційних та надлишкових розрядів має назву завадостійкого коду.

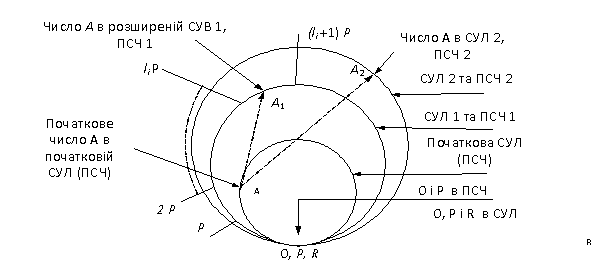
Рисунок 3 - “Блукання” точки, що відображає число А, по числовим кільцям, що дотикаються в точках А = 0 (Р, R)

Розглянемо випадок щодо представлення початкового числа А (слова для шифрування) в деяких системах числення (незалежно від того, ПСЧ, СЛК чи СУЛ). Нехай для визначеності це число А буде в наданим у початковій системі числення (на рис. 2, 3 це позначено точкою А в початковій СУЛ (ПСЧ)) у вигляді:

А = α₁, α₂, α₃, ..., α_n,

де α_і-і- та складова початкового числа А та, одночасно, - умовний “лишок” від ділення А на р_і. Як відомо, в цій системі числення однозначне представлення чисел є можливим при умові А ≤ Р.

Нехай збільшення кількості основ у СУЛ здійснюється за рахунок введення додаткової основи р_k. При цьому діапазон представлення чисел розширюється до R = Р∙р_k, тобто складається із р_k піддіапазонів Р. Для представлення числа А в розширеній СУЛ слід якимось чином задати лишок А по цій новій основі - величину α_k. Із теорії лишкових класів відомо, що в разі визначення величини α_k як:

,

число

А = α₁, α₂, α₃, ..., α_n, α_к

залишається в першому (“робочому”) діапазоні (0, Р] розширеного діапазону
(0, R), якщо ж α_k ≠ , а дорівнює, наприклад, α_k = х, число А виходить поза межі робочого діапазону і попадає в інший діапазон, наприклад, в діапазон (див. рис. 2, 3).

Тобто, за рахунок додавання замість “правильного” лишку по основі р_k іншого (наприклад, випадкового чи помилкового числа α_k = х по цій же основі) здійснюється “викид” вихідного числа (точки А₁ чи А₂ на рис. 2) із робочого діапазону [0, Р) у випадковий діапазон, наприклад, в діапазон (l_i∙Р, (l_i+ 1)∙Р) в межах діапазону [0, R). Таке переміщення точки А по числовим кільцям можна вважати випадковим “блуканням”. При цьому в СУЛ таке число записується у вигляді

= α₁, α₂, α₃, ..., α_n, х.

До речі, такий “викид” буде спостерігатися і при модифікації лишку по будь-якій іншій основі. Визначити номер l_і, в який потрапляє число А при спотворенні лишку по будь-якій основі, наприклад, по основі р_і, можна наступним чином. Спотворення по одній з основ у СУЛ має вигляд:

(α₁, α₂, α₃, ..., α_i-1, х, ..., α_k) - (α₁, α₂, α₃, ..., α_i-1, α_i, ..., α_k) = 0, 0, ..., , ..., 0.

Числа такого виду, які мають в СУЛ усі лишки окрім одного (в цьому випадку -р_і) такими, що дорівнюють нулю, є числами кратними усім основам системи числення за виключенням основи р_і. Тобто, є числами виду

= ,

тоді:

= ,

звідкіля

= .

Тобто здійснивши “випадкове”, але відоме на передаючому боці, спотворення лишку по певній основі, досить просто знайти номер того інтервалу, куди попаде у своєму “блуканні” спотворене число.

Із рис. 2, 3 видно що:

.

Останнє, у свою чергу, при визначених та дозволяє досить просто визначити величину “спотворення” Δα_і = :

Δα_і = = =

і здійснити, при потребі, корекцію цього “спотворення”

α_і = .

Розглянута властивість точок, що “блукають” по кільцях систем числення, надає можливість побудови криптосистем із несиметричними (відкритими) ключами.

1. Василенко В.С. Варіант завадостійкого криптографічного перетворення. /В.С.Василенко, В.М.Горицький // “Современные проблемы телекоммуникаций”, збірка доповідей на 6 – ій міжнародній науково - технічній конференції, 19 - 22 серпня 2003 р. (ч. 1) // Одеська національна академія зв’язку ім. А.С. Попова - с. 71 - 73.

2. Василенко В.С. Варіант завадостійкого криптографічного перетворення. / В.С.Василенко // Правове, нормативне та метрологічне забезпечення системи захисту інформації в Україні, вип.. 8, 2004 р. - с. 101 - 108.

3. Коржов В. Асимметричные криптоалгоритмы./В. Коржов// Открытые системы. № 7- 8/2002.