К.ф.-м.н. Бозиев О.Л.

Кабардино-Балкарский государственный университет (г.Нальчик, Россия)

О приближенных решениях краевых задач для параболических уравнений со степенной нелинейностью

В области Q = {(x, t): 0 < x < l, 0 < t < T} при натуральном p > 1, рассмотрим квазилинейное уравнение со степенной нелинейностью вида

, (1)

в котором

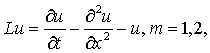
– линейный дифференциальный оператор параболического типа. Требуется найти интегрируемую функцию , удовлетворяющую уравнению (1) в области Q, а также начальному условию

(2)

и одному из следующих типов граничных условий

(3)

(3¢)

При этом , .

Способ решения задачи (1) – (3) путем аппроксимации нелинейного уравнения (1) соответствующим нагруженным дифференциальным уравнением описан в [1]. В общих чертах он сводится к последовательному приближению к решению уравнения (1) путем решений уравнений вида За начальное приближение принимается решение уравнения где . Применение данного способа позволяет получить формулы общих членов последовательностей приближенных решений исходной задачи. Некоторые из них для случая однородных начальных и краевых условий приведены в [2]. Приведем примеры приближенных решений для неоднородного начального и однородных граничных условий.

1. Рассмотрим задачу (1), (2), (3) в которой l = p, p = 2. Положим j(x) = sinx, y₁(t) = y₂(t) = 0. Проинтегрируем дважды по x уравнение используя условия (3) найдем δ = –12/p². Для нахождения начального приближения получаем задачу

. (4)

Ее решение найдем с помощью формулы Грина для параболического уравнения (см. [1]):

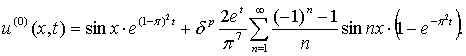
Найденную функцию примем за нулевое приближение в итерационном процессе «уточнения» приближенных решений рассматриваемой задачи, состоящем в последовательном решении линейных задач

(5)

. (6)

начиная с k = 1. В частности, очередное приближение определяется выражением

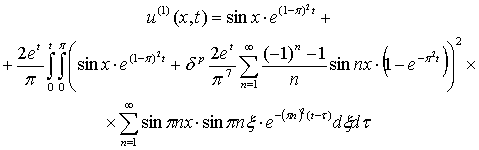(7)

Вычисление интегралов в (7) и использование итерационного процесса (5) – (6) позволяет получить более “точные” приближенные решения задачи (6) для уравнения (1) с p = 2.

2. Рассмотрим задачу (1), (2), (3¢) в которой l = 1, p = 2. Пусть j(x) = 2x, y₁(t) = y₂(t) = 0. В этом случае δ(t) = 1, а для нахождения нулевого приближения u⁽⁰⁾ получаем задачу

u⁽⁰⁾(x, 0) = 2x, u_x⁽⁰⁾(0, t) = 0, u_x⁽⁰⁾(l, t) = 0.

Ее решение с помощью соответствующей формулы Грина дает

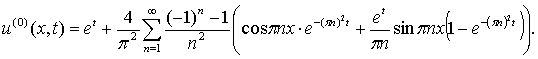
Очередное приближение будет найдено после вычисления интегралов в выражении

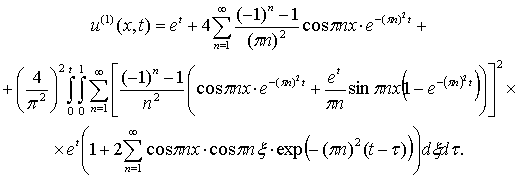(8)

Аналогично предыдущему случаю, отталкиваясь от (8) можно получить любое количество приближений к точному решению рассматриваемой задачи

Литература

1. Бозиев О.Л. Решение начально-краевой задачи для нелинейного параболического уравнения методом редукции к нагруженному уравнению // Известия КБНЦ РАН. – 2012 – № 4(48) – с. 20 – 25.

2. Бозиев О.Л. Построение приближенных решений краевых задач для нелинейных дифференциальных уравнений методом редукции к нагруженным уравнениям // Материалы международного симпозиума «Устойчивое развитие: проблемы, концепции, модели», посвященной 20-летию КБНЦ РАН. Россия, Нальчик, 28 июня – 3 июля 2013 г. Т. 2, с. 84 – 87.