И.А. Долгарев, А.И. Долгарев

ГАЛИЛЕЕВА ГЕОМЕТРИЯ ПОДОБИЙ. ДВИЖЕНИЯ ПО ТРАЕКТОРИЯМ

ПОДОБИЙ. РАСШИРЯЮЩЕЕСЯ ПРОСТРАНСТВО

Геометрия одного из ВО-пространств является галилеевой геометрией подобий, она осуществлена в аксиоматике Г. Вейля на одуле Ли, называемом растраном – одуле Ли гомотетий и переносов. Траектории растрана экспоненциальны или прямолинейны. Скорость движений материальных точек по траекториям в геометрии подобий не совпадает со скоростью движений по тем же траекториям в евклидовом пространстве. Относительно движений по линейным траекториям галилеево пространство подобий является расширяющимся с увеличивающимися скоростями, т.е. с красным смещением.

1. Пространство-время с растраном

1.1. Некоммутативность геометрии подобий

В основе геометрии подобий лежит растран, который состоит из расширений (гомотетий) и трансляций (параллельных переносов) аффинного пространства. Композиция гомотетий является либо гомотетией, либо параллельным переносом. Существует группа гомотетий с фиксированным центром, но гомотетии с различными центрами приводят к параллельным переносам. Группа подобий является расширением группы движений группой гомотетий. Как евклидова геометрия основана на группе параллельных переносов, так и геометрия подобий основана на группе гомотетий и переносов. На группе переносов и гомотетий определена внешняя операция. Композиция преобразований считается их суммой; определена операция умножения гомотетий на действительное число, а умножение на действительное число параллельных переносов уже известно. Группа гомотетий и переносов с внешней операцией обобщает линейное пространство, называется растраном и относится к одулям Л.В. Сабинина, [1, 2]. В настоящее время разработана галилеева геометрия с растраном, она изложена в [2]. Группа гомотетий и переносов некоммутативна, поэтому геометрии пространств с растраном некоммутативны, в частности, галилеева геометрия подобий некоммутативна.

Ранее, в [3], проведено сравнение геометрии галилеевых движений и геометрии параллельных переносов, т.е. евклидовой геометрии. Оказалось, что скорость движения материальной точки по траекториям галилеевых движений может быть больше или меньше скорости движения по тем же траекториям в евклидовом пространстве, [3, теорема 5]. Ниже рассмотрены скорости движений по траекториям подобий и в евклидовой геометрии. Установлено, что относительно движений по линейным траекториям галилеево пространство подобий является расширяющимся: от всякой точки этого пространства все точки движутся со все возрастающими скоростями.

1.2. Растран и его сетевые уравнения

Геометрия пространства с растраном впервые рассмотрена в [4], где содержится и арифметическая модель растрана. Наличие модели свидетельствует о непротиворечивости геометрии подобий. На многообразии однородный растран задается операциями

, (1)

. (2)

[2, c. 107]. Элементы растрана называются растами, растран обозначается . Нулевой раст есть ; раст, противоположный расту , равен

.

Расты вида = составляют линейное пространство над как 2-мерный подрастран в , это линейное пространство параллельных переносов. Всякий раст обладает разложением

=;

расты , , составляют базис растрана. Выполняется соотношение

=,

т.е. раст , , задает на линейном пространстве гомотетию с коэффициентом . Расты составляют подрастран , являющийся 1-мерным линейным пространством над , это линейное пространство гомотетий с общим центром. Растран является расширением линейного пространства линейным пространством :

=┤,

это полупрямая сумма линейных пространств, [2, c. 111]; растран относится к двухступенно разрешимым 3-мерным одулям Ли.

Пусть 1-мерное подпространство в . Имеются смежные классы , . Если в некотором базисе , , , то сетевые уравнения линейного пространства таковы

.

[2, c. 249]. В растране всякий 1-мерный подрастран является линейным пространством. Смежные классы по =, есть , [2, c. 248 – 249]. Если в базисе растрана : , , , то сетевые уравнения растрана записываются по операциям (1) и (2):

. (3)

Уравнения экспоненциальны и имеют вид . Если , т.е. раст является вектором, то уравнения принимают вид

,

[2, c. 250]. Таким образом, для векторов из растрана сетевые уравнения такие же, как для линейного пространства и уравнения сети линейны.

1.3. Галилеева норма растов. Дифференцирование ратранных функций

Галилеевой нормой раста называется число

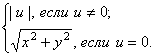(4)

см. [2, c. 120 – 121], галилеева норма растов определена на основе их галилеева скалярного произведения. Это аналог расстояния в пространстве-времени Галилея, [5, c. 843 – 844]. Если еще один раст, то по (1) и (2) получаем

. (5)

В этом случае по (4):

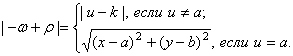(6)

Растранную функцию можно рассматривать в виде:

= , . (7)

В [6] вычислена производная растранной функции, см. также [2, c. 125 – 126]:

= . (8)

Имеем: . В частности,

. (9)

1.4. Пространства с растраном

В [2, c. 128 – 138] в аксиоматике Г. Вейля построена геометрия пространства с растраном . Это одно из ВО-пространств, называется ЛМ-пространством и обозначается , [6]. Паре точек и соответствует раст

, (10)

см. (5). Прямая линия ЛМ-пространства определяется точкой и растом : = . Пусть . Уравнения прямой:

, (11)

[2, c. 136]; это сетевые уравнения (3) растрана. (Обозначения в (3) и (10) изменены по сравнению с [2].) Если точка вне прямой и , то существуют две различные прямые, проходящие через точку и параллельные прямой , [2, c. 129 – 130]. Пространство с некоммутативным одулем, в нашем случае с растроном, является гиперболическим.

Если для растов введена галилеева норма, то имеется ВО-пространство с раст-раном, обладающее метрическими свойствами. Оно называется ЕМ-пространством и обозначается . Согласно (4), первую компоненту растов и точек считаем временной, обозначаем , вторая и третья компоненты растов и точек считаются пространственными. Пространство с нормированным растраном является галилеевым пространством-временем. Геометрия пространства-времени некоммутативная, это галилеева геометрия подобий.

1.5. Движения по траекториям в ЕМ-пространстве

Кривая ЕМ-пространства-времени описывается растранной функцией

= , . (12)

Считается, что кривая регулярна класса , т.е. функция не менее трех раз дифференцируема, . Точки регулярной кривой называются обыкновенными. Временной параметр для кривой (12) является естественным. Расты производных функции (12) есть (8) и (9). Прямая линия в естественной параметризации есть

,

по сравнению с (11): . Прямая ЕМ-пространства описывается функцией вида

= , (13)

уравнения экспоненциальны, при линейны. По (8), (9):

= , . (14)

Всякая точка пространства-времени является событием, множество всех событий есть мир. Если событие принадлежит линии (12), то (12) называется мировой линией события . Ввиду разложения растов по базису, имеем для мировой линии (12):

= = , (15)

= . (16)

Множество всех событий , одновременных с событием , характеризуется, согласно (10), растами

,

все эти расты являются векторами из , и, по (4), все события составляют евклидову плоскость в ЕМ-пространстве-времени. Через всякую точку в проходит единственная евклидова плоскость. Функция (16) описывает линию в евклидовой плоскости = ЕМ-пространства-времени , проходящую через начало отсчета . Кривая (16) является проекцией мировой линии (12) события в евклидову плоскость , и (16) является траекторией события . Имеем

1. ТЕОРЕМА. Траектории подобий есть евклидовы прямые.

# По разложению (15) для (13) имеем , откуда . #

Производная по времени мировой линии (12) события определяет скорость движения точки по траектории . По (16) и (13) имеем

= .

Следовательно, скорость движения точки по траектории (16) в ЕМ-пространстве-времени описывается векторной функцией

= . (17)

Символ означает функцию скорости в пространстве с растраном . Выполняется

2. СВОЙСТВО. Вектор скорости движения точки по траектории в ЕМ-

пространстве есть (17), его обе пространственные координаты зависят соответственно от компонент траектории и их производных; в результате дифференцирования функции мировой линии движения в пространственных компонентах появляется множитель . # Отметим, что .

Если же траектория движения точки рассматривается в евклидовом пространстве , а не в ЕМ-пространстве-времени, то скорость движения по этой траектории есть . Выполняется

3. СВОЙСТВО. Вектор скорости при движении в евклидовом пространстве отличается от вектора скорости в ЕМ-пространстве . #

Мы получили следующий факт.

4. ТЕОРЕМА. Скорость движения по траектории в ЕМ-пространстве-времени есть (17) – разность вектора евклидовой скорости и вектора , умноженная на коэффициент . #

1.6. Движение по траекториям растрана

По теореме 1, траектории растрана есть прямолинейные траектории ЕМ-прост-ранства. В движениях с прямолинейной мировой линией (13) траектория описывается функцией = , она прямолинейна, см. доказательство теоремы 1. Согласно (15) и (17), скорость по траектории (18) постоянна и равна = , . Ускорение движения равно нулю.

5. ТЕОРЕМА. В галилеевом пространстве подобий движения по траекториям растрана прямолинейны, скорости движений материальных точек постоянны, ускорение отсутствует. #

1.7. Движения в одулярных пространствах

И в пространстве-времени с сибсоном [3], и в пространстве-времени подобий с растраном траектории соответствующих одулей Ли прямолинейны в своих пространствах, как и траектории параллельных переносов в евклидовом пространстве; но в ЕС- ЕМ- пространствах прямые описываются нелинейными уравнениями. Геометрии пространств галилеевых движений и подобий некоммутативны, скорости движений материальных точек по траекториям указанных галилеевых пространств отличаются от скоростей движений, описываемых средствами евклидовой геометрии.

2. Расширяющееся пространство

2.1. О геометрии многообразия

В [7] рассмотрен один из аспектов геометрии многообразия . В линейном пролстранстве аффинного пространства определены различные скалярные произведения векторов: собственно евклидово, псевдоевклидово, галилеево и т.д.. Аффинная геометрия изучает свойства фигур, не связанные с метрическими понятиями. Метрику, квазиметрику и т.д. можно ввести в пространство, определяя в скалярное произведение векторов. Аффинные объекты, после введения скалярного произведения векторов, выявляют свои метрические свойства. Определяя собственно евклидово скалярное произведение векторов, мы получаем возможность изучать евклидовы свойства объектов, в частности, кривых. Определив галилеево скалярное произведение векторов, мы выявляем галилеевы свойства объектов, среди них кривых. Одни и те же кривые обладают аффинными, евклидовыми, галилеевыми свойствами. Но изучаются указанные свойства кривых различными средствами: аффинными, евклидовыми, галилеевыми. Аффинные прямые остаются прямыми и в евклидовой геометрии и в галилеевой геометрии. Этот факт зависит от операций над векторами в ; операции коммутативны и линейны.

На помимо структуры линейного пространства определены и некоммутативные алгебраические структуры – одули Ли, [2, c. 102 – 121], среди них структура растран. Прямые в пространствах с линейным пространством (в аффинном пространстве) описываются линейными функциями . Прямые в пространствах с растраном описываются в общем случае экспоненциальными функциями (13), растран на задан нелинейными операциями (1) и (2). Геометрия многообразия зависит от операций алгебраической структуры, на которой строится геометрия (речь идет об их общей аксиоматике – аксиоматике Г. Вейля).

2.2. Расширение пространства с растраном

В ЕМ-пространстве-времени рассмотрим непрямолинейные мировые линии, заданные линейными функциями

= , ; (18)

прямолинейные мировые линии событий из описываются функциями (3). Тогда, по (8), в ЕМ-пространстве-времени

=

и при в каждой компоненте является возрастающей линейной функцией, , ускорение движения по рассматриваемой траектории постоянно и равно

;

а в евклидовом пространстве по траектории = евклидова скорость есть и постоянна.

6. ТЕОРЕМА. В ЕМ-пространстве-времени в движениях по мировым линиям вида

(18) из любой точки во всех направлениях с увеличением времени движения скорость движения точек неограниченно увеличивается, т.е. ЕМ-пространство-время является разбегающимся.

# В движении по мировой линии (18) скорость движущейся точки возрастает при удалении о начала отсчета (от значения ), т.е. увеличивается со временем. На том же многообразии , совпадающем с , имеет место еще аффинная геометрия, см. п.2.1, никак не связанная с геометрией пространства . Функция (18) в аффинной геометрии определяет прямую с вектором . Значит, в через всякую точку проходит линия (18) во всяком направлении. Расширение пространства происходит от точки при в (18) во всех направлениях , кроме направления, лежащего в плоскости ЕМ-пространства. Для вектора из растрана , как отмнчено в п. 1.2, в плоскости выполняется равенство

=, ,

т.е. и в евклидовой плоскости ЕМ-пространства-времени происходит увеличение расстояний с увеличением значения . Следовательно, и по мировым линиям в направлениях происходит увеличение скорости движения, т.е. происходит расширение, ускоряется разбегание точек. Точки ЕМ-пространства-времени разбегаются с увеличивающейся скоростью по мере удаления от начала отсчета. Началом отсчета может быть выбрана любая точка. Разбегание точек происходит от любой фиксированной точки. #

Разбегание ЕМ-пространства проиходит по линиям (18). Результат обеспечивается выбором линий, описываемых линейными функциями. В ЕМ-пространстве-времени определены метрические понятия, что позволяет дифференцировать растранные функции. Обнаружены мировые линии и траектории точек в , проходящие через всякую точку во всех направлениях, в движениях по которым происходит разбегание точек с увеличивающейся скоростью. Линии (18) бесконечны, при движении по ним увеличение пространства не происходит. Описываемый процесс напоминает разбегающуюся Вселенную со всеувеличивающейся скоростью, т.е. с красным смещением.

Литература

1. Сабинин Л.В. Одули как новый подход к геометрии со связностью // ДАН СССР. 1977. N5. C.800-803.
2. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005. – 306 с.
3. Долгарев И.А., Долгарев А.И. Геометрия галилеевых движений в сравнении с геометрией параллельных переносов. // Материали за IX международна научна конференция «Ключови въпроси в съвременна наука наука», 2013. Том 33. Физика. Математика. София. «Бял ГРАД-БГ» ООД, 2013. С. 3 – 11.

4. Долгарев А.И. ЛМ-пространство //Римановы пространства и методы эллиптических дифференциальных уравнений. Л.: ЛГПИ, 1986. - С. 8 – 25.

5. Математическая энциклопедия, Т.1. – М. Советская энциклопедия, 1977. – 1152с.

6. Долгарев А.И. ЕМ-пространства. Дис... канд. физ.-мат. наук, Красноярск: КГПИ, 1991.- 95 с.

7. Долгарев А.И. О геометрии 3-мерного действительного многообразия. – Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2010, вып. 1(23). – С. 2 – 19.