Д.т.н. Володин Г.Т., Новиков А.С.

Тульский государственный университет, Россия

Метод Б.Г. Галеркина в задачах гарантированного разрушения оболочечных конструкций взрывом

Нахождение условий разрушения оболочечных конструкций является актуальной проблемой при проектировании несущих элементов конструкций взрывоопасных производств, определении технических условий при проектировании складов боеприпасов, утилизации крупногабаритных элементов конструкций, при проектировании взрывозащитных инженерных сооружений и др. Важно определить форму и величину заряда взрывчатого вещества (ВВ), при взрыве которого на некотором расстоянии от оболочечной конструкции, гарантированно произойдет её разрушение. Под разрушением понимаем потерю несущей способности оболочки вследствие появления в ней трещин, сколов, разделений на фрагменты.

Физическая модель (основные допущения)

Рассмотрим задачу о нахождении необходимой массы С заряда ВВ для гарантированного разрушения открытой цилиндрической оболочки (рисунок 1).

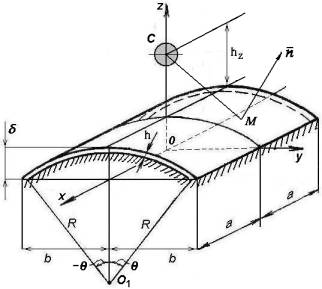
Рисунок 1 – Схема расположения заряда ВВ над оболочкой при взрыве

Оболочка, с размером плана 2а×2b м, выполнена из упругого материала (серый чугун марки СЧ 24 - 44), имеет постоянную толщину h, радиус кривизны R и шарнирно оперта по всему своему контуру. Оболочка принимается тонкой и пологой, т.е. [1] и [6] соответственно. Материал оболочки предполагается однородным и изотропным. Рассматривается упругий режим деформирования вплоть до ее разрушения. Принимаются основные классические гипотезы теории тонких оболочек [1]. Прогибы оболочки предполагаются малыми, не превышающими 1/5 ее толщины. На расстоянии h_Z от срединного слоя оболочки, над центром симметрии плана, располагается сосредоточенный сферический заряд взрывчатого вещества радиуса r₀, тип и энергетические характеристики которого определяются обобщенным параметром А₀. В качестве ВВ возьмем литой тротил с плотностью ρ₀ = 1630 кг/м³ и А₀ = 400 м/с [2]. Рассматривается ближняя область действия взрыва [2], для которой давлением окружающей среды можно пренебречь по сравнению с давлением продуктов взрыва. Вследствие кратковременности действия взрывной нагрузки (время её действия не превышает 2×10^-4 с) начальными смещениями точек пластины, за время действия нагрузки, можно пренебречь [5].

Математическая модель и решение задачи

Введем прямоугольную декартову систему координат Oxyz с началом в центре симметрии плана оболочки (рисунок 1). Обозначим δ – стрелу подъема оболочки над планом, , О₁ – центр кривизны, 2θ – угол, определяющий длину дуги цилиндрической оболочки радиуса R.

Оболочка имеет геометрические и механические характеристики: a = 0,75 м, b = 0,5 м, R = 2 м, h = 4·10^-2 м, δ = 6,4·10^-2 м, h_Z = 0,3 м, плотность чугуна ρ = 7,2·10³ кг/м³, коэффициент Пуассона μ = 0,24, модуль Юнга Е = 1,33·10¹¹ Па, коэффициент однородности на гарантированное разрушение К_0* = 1,4, коэффициент динамичности µ₃ = 1,3, предел прочности на одноосное растяжение σ·^р = 2,4·10⁸ Па и на сжатие σ·^с = 8,5·10⁸ Па.

Согласно принятым допущениям, деформирование оболочки происходит уже после действия взрывной (импульсной) нагрузки, в течение свободных колебаний, которые описываются уравнением

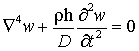, (1)

где D = Eh³/[12(1-µ²)] – цилиндрическая жесткость, w = w(x, y, t) – прогиб произвольной точки M(x, y). Начальные условия для уравнения (1) имеют вид:

w(x, y, 0) = 0, (2)

, (3)

где удельный импульс i, действующий в ближней зоне, может быть вычислен, согласно исследованиям Т.М. Саламахина [2, 5], по формуле

, (4)

где r – расстояние от точки М до центра заряда ВВ, φ – угол падения (угол образованный скоростью потока продуктов взрыва с нормалью к поверхности преграды). Начальные скорости точек оболочки V = i/ρh, с учетом (4), выразятся в виде

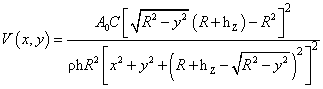. (5)

Обозначим V(x, y) = C·V₁(x, y), где

.

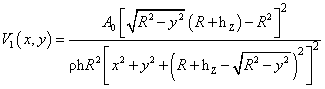Граничные условия соответствуют способу закрепления. Для шарнирно опертой по всему своему контуру оболочки получим

при x = ± a, (6)

при y = ± b. (7)

Для решения поставленной задачи, определяемой уравнением (1), начальными (2), (3) и граничными условиями (6), (7), применим приближенный метод Б.Г. Галеркина [9]. Функцию w(x, y, t) будем искать в виде

(8)

Функция w(x, y, t), определяемая выражением (8), удовлетворяет граничным условиям. Введем обозначения

,.

Начальное условие (2) выполняется, если с₁(0) = 0 и с₂(0) = 0. Обозначим и . Найдем из (8) выражение подставим в начальное условие (3). Получим невязку, которую будем минимизировать следующим образом

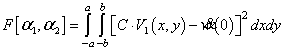. (9)

Соответствующие преобразования приводят выражение (9) к виду

,

где

, , ,

, , .

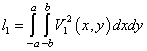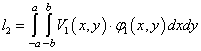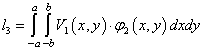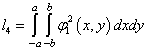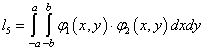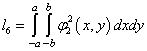Решая систему уравнений и , получаем

, .

Таким образом, полностью находим начальные условия для выражения (1). Подставляя (8) в (1), так же получаем невязку N(x, y, t).

Помножив N(x, y, t) на координатные функции φ₁(x, y), φ₂(x, y) и проинтегрировав полученные выражение по площади плана оболочки [8], придем к системе уравнений

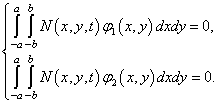(10)

Система (10) преобразуется к виду

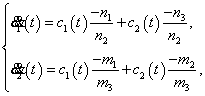(11)

где , , , , , ,

, , , , , ,

, .

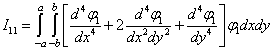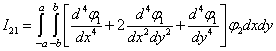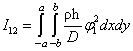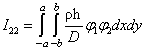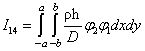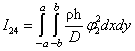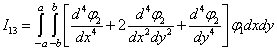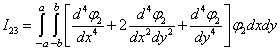Решая систему дифференциальных уравнений (11), найдем выражения для с₁(t) и с₂(t), графики которых для промежутка времени то 0 до t₁ = 0,002 с показаны на рисунке 2А. Для момента времени t₁ график функции w(x, y, t), определяющий прогибы, представлен на рисунке 2Б. В любой момент времени максимальный прогиб оболочки w_max будет находиться в точке с координатами x = 0, y = 0; график движения точки с указанными координатами до момента времени t₁ представлен на рисунке 3. Первое амплитудное колебание происходит в момент времени t_* = 0,0008 c (определено графическим способом). Подставим полученное таким образом приближенное решение w(x, y, t) в выбранный критерий разрушения, предложенный П.П. Баландиным [7], в котором учтем динамический характер действующей нагрузки. Согласно введенным ранее основным гипотезам теории тонких оболочек и динамике внешнего воздействия, этот критерий приводит к соотношению

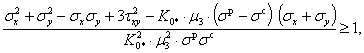(12)

где для срединной поверхности имеем

(13)

Подставив (13) в (12), получим выражение вида . Минимальную массу С заряда ВВ определим исходя из того, чтобы оболочка гарантированно разрушилась, т.е. выполнилось равенство в выражении (12), в момент времени t_* = 0,0008 c (в первом амплитудном колебании). Это масса будет равна 1,2 кг. Пересечение поверхностью Ω(x, y, t) плоскости Ω₁(x, y) = 1 в момент времени t_* (при найденной массе С = 1,2 кг) показано на рисунке 4А, а линии уровня поверхности Ω(x, y, t) в тот же момент времени на рисунке 4Б. Сравнение скорости V(x, y) из (5), при массе С = 1,2 кг, со скоростью приведено на рисунке 5.

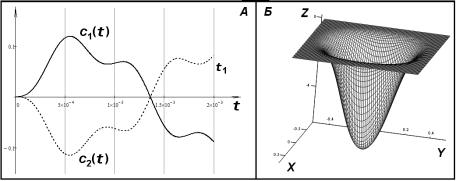
Рисунок 2 – Графики с₁(t), с₂(t) и w(x, y, t)

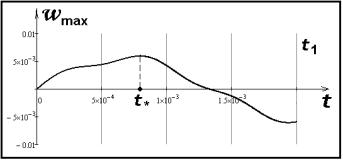
Рисунок 3 – График w_max

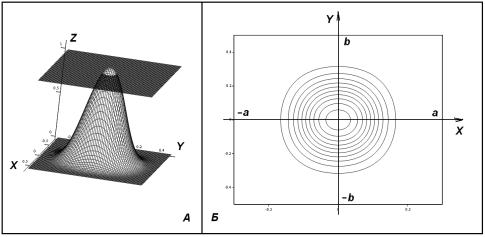
Рисунок 4 – Графики поверхности Ω(x, y, t) и ее линий уровня

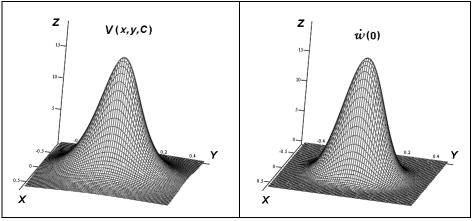
Рисунок 5 – Сравнение скоростей V(x, y) и

Отношение максимального прогиба к толщине оболочки, в момент времени t_*, будет равно w_max/h = 0,148. Данная величина не превышает 1/5, что соответствует введенной гипотезе малых прогибов.

Таким образом получены соотношения, позволяющие определить по известным физическим и геометрическим характеристикам оболочечной конструкции, способу ее закрепления на опорах, минимальную массу заряда ВВ данного типа, взрыв которого на заданном расстоянии от оболочки приводит к ее гарантированному разрушению. Методика проведенных исследований может быть использована для инженерных расчетов в задачах прогнозирования гарантированного разрушения элементов конструкций взрывом неконтактных зарядов ВВ.

Библиографический список

1. Новожилов В.В. Теория тонких оболочек. Л.: ГСИСП, 1962. – 432 с.

2. Саламахин Т.М. Физические основы механического действия взрыва и методы определения взрывных нагрузок. М.: ВИА, 1974. – 255 с.

3. Володин Г.Т. Действие взрыва зарядов конденсированных ВВ в газовой и жидкой средах. Часть 2. Взрывостойкость и гарантированное разрушение элементов конструкций. Тула: Левша, 2005. – 160 с.

4. Володин Г.Т. Прямой вариационный метод исследования взрывостойкости и гарантированного разрушения балочных конструкций взрывной нагрузкой // Вестник Тульского государственного университета. Серия Дифференциальные уравнения и прикладные задачи. Вып. 1. – 2009. – С. 49–54.

5. Саламахин Т.М. Разрушение взрывом элементов конструкций. М.: ВИА, 1961. – 275 с.

6. Колкунов Н.В. Основы расчета упругих оболочек. М.: Высшая школа, 1963. – 278 с.

7. Гольденблат И.И., Копнов В.А. Критерии прочности и пластичности конструкционных материалов. М.: Машиностроение, 1968. – 191 с.

8. Флетчер К. Численные методы на основе метода Галеркина. М.: Мир, 1988. – 347 с.

9. Галёркин Б.Г. Собрание сочинений. М.: Изд-во АН СССР, Т.1 – 1952. – 391 с., Т.2 – 1953. – 438 с.