Бойко О. Р., Квєтний Р.Н., Степова Т. О.

Вінницький національний технічний університет

Вирішення задач апроксимації експериментальних даних, отриманих в умовах невизначеності

У зв’язку з розвитком таких напрямів науки і техніки, як механіка, теплотехніка, математична хімія, літакобудівництво, виникла необхідність обчислення не тільки наближених рішень різноманітних задач, але й гарантованих оцінок їх близькості до точних рішень. Використання методів інтервальної математики дозволяє не лише представити опис невизначених даних, а й врахувати неточність результатів обчислювальних операцій, що значно полегшує подальший аналіз достовірності даних. Інтервальні методи можуть бути використані для розв’язку таких проблем управління, як робастні аналіз та управління, інтервальне імітаційне моделювання і цифрове управління в умовах невизначеності.

В багатьох інженерних задачах засоби знаходження аналітичного виразу невідомої залежності грають напрочуд важливу роль, діяльність інженера є неможливою без знаходження закономірностей та оцінки точності розрахунків проведених операцій. Засобами апроксимації здійснюється обробка експериментальних даних в задачах ядерного магнітного резонансу в хімії, їх використовують при сліпому розділі сигналів в МІМО в системах передачі інформації, обробці сигналу в інженерній практиці, томографії мозку і внутрішніх органів в медицині, в задачах ідентифікації голосу або образу та інших напрямках науки і техніки.

Важливим фактором також є те, що попри широке використання методів апроксимації, традиційні підходи не враховують умов певної невизначеності, при яких отримуються експериментальні дані, що забезпечують похибку, яка, в свою чергу, не враховується при вирішенні задач апроксимації. Даний фактор є суттєвим недоліком при вирішенні задач, в яких особливе місце займає прогнозована точність, достовірність оцінки похибки. Ось чому перспективним є поєднання принципів інтервальної математики та методів обробки експериментальних даних, що дає можливість отримати потужний інструмент для застосування в інженерній практиці, вдосконалити існуючі засоби, запровадити більш уважний підхід до наближень та мати гарантовану достовірність отриманих результатів. Тому розробка методів апроксимації на основі інтервальних даних є актуальною науковою задачею.

Інтервалом називається деякий відрізок дійсної вісі, що має верхню та нижню межу. Найпростішим апаратом для оперування з ними є класична інтервальна арифметика, більш досконалою є арифметика Каухера, особливістю якої є наявність інтервалів, де нижня границя не обов’язково має бути меншою за верхню та низка додаткових властивостей, що значно розширюють спектр операцій над інтервалами.

Було запропоновані наступні нововведення для підвищення достовірності апроксимації. Було введено правила інтервальної класичної арифметики при виконанні дій над інтервалами. І, зважаючи на нескладність необхідних операцій було обрано саме класичну інтервальну арифметику, так як при дослідженні методу за використанням інтервальної арифметики Каухера було отримано ті ж результати але з ускладненням алгоритму та логіки методу.

Для розв’язку отриманої в інтервальному вигляді системи лінійних рівнянь, було модифіковано метод Гаусса, до вигляду показаного на рисунку 1.

Також запропоновано перехід від інтервальної до точної моделі, за використанням середнього значення інтервалу, що ґрунтується на намаганні зрівноважити похибку з обох боків значення.

Тестування розроблених методів було проведено на значеннях моніторингу споживання холодної та гарячої води у багатоквартирних будинках за місяць. В результаті коефіцієнти поліноміальної апроксимації за інтервальними вхідними даними містили в собі значення коефіцієнтів поліноміальної апроксимації за точними вхідними даними. При переході до точних значень було отримано, що апроксимуюча функція, побудована з коефіцієнтів рівних значенню середнього отриманих інтервалів, не виходить за межі вхідних значень. Більш того, максимальне відхилення середніх значень інтервалів апроксимуючої функції не перевищувало значення 0.03, яке дає змогу стверджувати, що маючи лише набір можливих значень функції і певній точці можна відтворити її з достовірністю гіршою за апроксимацію на точних даних на значення, не більше за це значення.

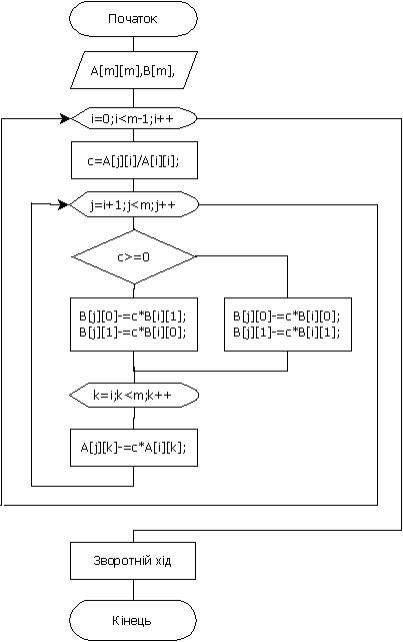
Рисунок 1 - схема алгоритму інтервального методу Гаусса

Отже, використання принципів інтервального аналізу є дієвим методом для включення у результати обрахунків точного вирішення задачі з урахуванням похибок обчислення, округлення, тощо. Також це ефективний підхід до вирішення задач з вхідними даними заданими в умовах невизначеності. Виконані дослідження дозволили на основі узагальнення відомих підходів і використання нових положень запропонувати нові алгоритми та методики для реалізації у інтервальній математиці методів поліноміальної апроксимації функції однієї і двох змінних.