29.00.00
Фундаментальная физика
УДК
530.18 (УДК 530.10(075.4))
Яловенко С.Н.,
Черный предел. Часть 11.
Плоский конусный взрыв при образовании чёрной дыры.
Гравитация как изменяющаяся плотность эфира.
В
предыдущих главах были получены расширенные формулы для гравитации:
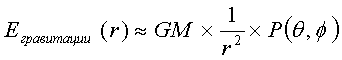 (1)
(1)
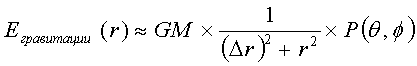 (2)
(2)
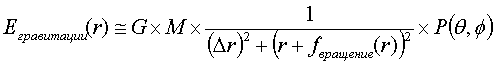 (3)
(3)
Для облегчения понимания расширенного
уравнения для гравитации (1-3), где формула 1/r2 изменена на формулу 1/(r+fвращение(r))2,
гравитацию можно представить как
стрельбу во все стороны с неподвижной и
вращающейся платформы (рис.1). В первом случае, когда платформа неподвижна,
плотность силы действия пуль пропорциональна 1/r2 , но когда платформа
вращается, траектория движения пули изменяется из-за вращения, т.е. длина
пробега пули увеличивается на fвращение(r) и коэффициент 1/r2 переписывается с учетом увеличения длины
пробега как 1/(r+ fвращение(r))2. В зоне совпадения 1, (рис.1.)
fвращение(r)≈0 из-за большой скорости пули и им можно
пренебречь, соответственно формула 1/(r+ fвращение(r))2 переходит в формулу 1/r2 .
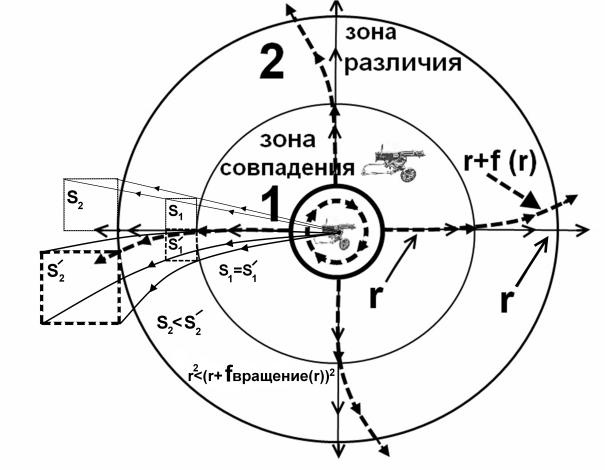
Рис. 1.Изменение гравитационного поля от расстояния.
а) б)
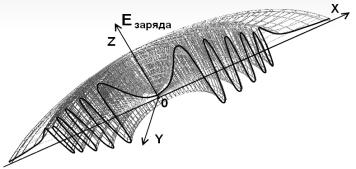
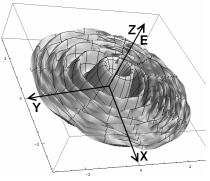
Рис.2. Графики изменения
напряженность электрического заряда элементарной частицы: а) срез изменения
напряженности элементарной частицы б) трехмерное представление напряженности
электрического заряда элементарной частицы
В зоне не совпадения 2 различия становятся
существенными, и пренебрегать ими нельзя. Напомним, что в водоворотной
криптоновой теории все частички представлены плоскими водоворотами (рис.2.а) и (рис.2,б.),
а гравитация рассматривается как суммарное изменение плотности крептона (эфира)
в пространстве и описывается формула(4).
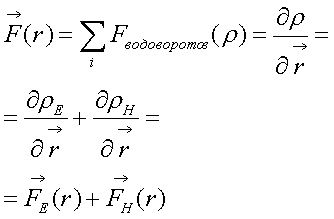 (4)
(4)
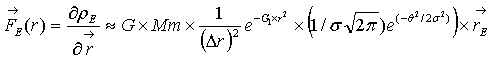 (4.1)
(4.1)
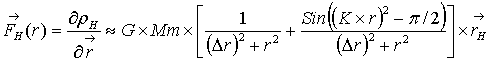 (4.2)
(4.2)
Где FE и FH
записаны приближённо и зависят от коэффициента сжатия, ρ –плотность эфира,
r – расстояние.
Для облегчения понимания второй части
формулы (1-3) гравитации Р ( θ , φ ) вероятностной функции
распределения, которая изменяет форму вида гравитации от сферической (форма
круга) к нормально распределённой форме (приближенно эллипсоидной на ранних этапах сжатия) по плоскостной составляющей FE=∂ρE /
∂r (для Е составляющей), можно предложить эксперимент со сферой
представленный на рисунках (рис.3,а,б.) и (рис.4).
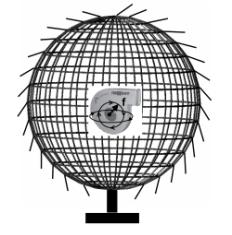
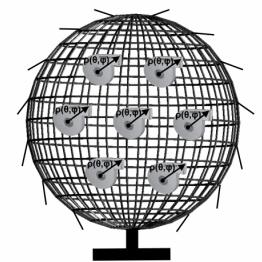
Эксперимент заключается в том, что в сферу
с наклеенными на её поверхность индикационными лентами помещаются плоские
вентиляторы (рис.3,а,б) или вращающиеся диски с выемкой, или пластиной на своей
поверхности (рис.4.). Эти вращающиеся диски вызывают эффект аналогичный плоским
вентиляторам, и создают модель изменения плотности (крептона, эфира) аналогичную
изменению плотности элементарной частицы представленной в крептоновой теории
плоскими водоворотами (рис.3,а,б).
а)
б)
Рис.3.Сфера для моделирования
и измерения гравитации: а) Сфера для моделирования гравитации для одной частицы
б) Сфера для моделирования действия гравитации для многих частиц.
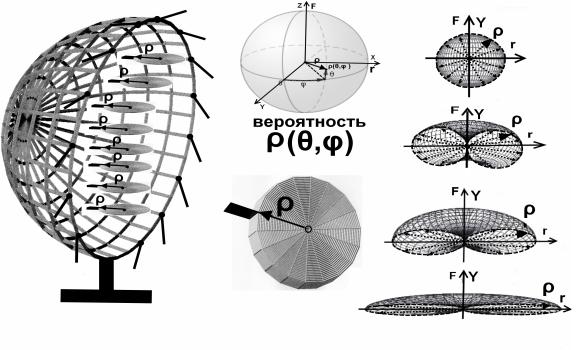
Рис. 4. Модель изменения
гравитации чёрной дыры для разных степеней сжатия.
При вращении плоскостных вентиляторов,
когда расстояние между ними велико и они не мешают друг другу, вероятностная
функция распределения вектора плоскости (XOY) ρ(θ,φ) равна Р(
θ , φ )=1, и индикационные ленты показывают сферическое распределение
силы (Ньютоновское, классическое ). По мере сжатия сферы, расстояния между вентиляторами
уменьшаются и когда оно становятся сопоставимыми с их размерами, то начинают
мешать друг другу, что приводит к изменению вероятностной функции распределения
вектора плоскости (XOY) ρ(θ,φ)
и Р( θ , φ )≠1. С учетом теплового движения (и других
факторов) функции распределения вектора плоскости (XOY), ρ(θ,φ),
Р(θ, φ ) от равномерного распределения будет переходить к нормальному
и индикационные ленты покажут изменение распределение силы (рис.4,5,в). Во
втором случае Р(θ, φ)=1 переходит в Р( θ, φ )=(1/σ√2π)ехр(-θ2/2σ2)
и распределение действия не будет соответствовать Ньютоновскому сферическому
распределению силы, что приведет к существенному суммарному отличию силы (рис.4.5,в,б.).
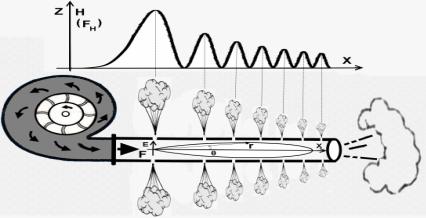
В данном эксперименте не учитывается изменение плотности перпендикулярной
плоскости (XOY) создающейся вектором Н, представленной функцией FH=∂ρH
/ ∂r , которая показана на рис.(5,а,б) жирной линией.
Более точную модель гравитации (с учетом FH
составляющей) можно получить если
заменить трубчатый вентилятор изображенный на (рис.3.а) на трубчатый вентилятор
с неравномерными прорезями создающими перпендикулярные потоки воздуха (модели
функции FH=∂ρH / ∂r ) относительно
основного потока воздуха (модели функции FЕ=∂ρЕ /
∂r). График силы, который при этом получится, показан на (рис.5.в.)
жирной линией.
а)

б)
в)
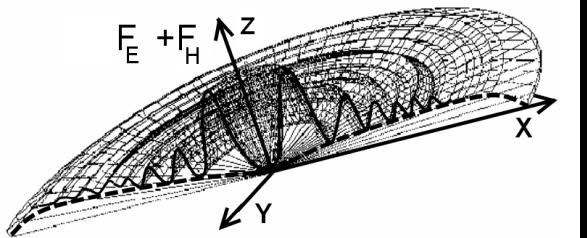
Рис.5. Графики суммарной плоской гравитации чёрной дыры:
а) Модель гравитации одной
частицы; б) трехмерное график гравитации чёрной
дыры; в) срез трехмерного
графика гравитации чёрной дыры
Компьютерное моделирование изменение гравитационной
силы при приближении массы к массе черной дыры при М→М чёрной дыры
без учета статистического размытия по Н составляющей рис.6 дает изменение гравитации показанной на рис.7. и является
аналогом графиков изображенных на рис.4.
а)

б) в)
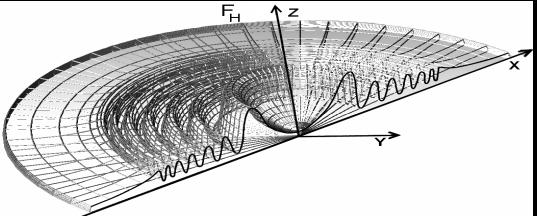
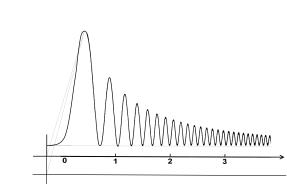
Рис.6. Гравитация, которую
создает Н составляющая. а) Трехмерный график гравитации FH. б) График гравитации FH на плоскости ZOX. в) График гравитации FH на плоскости ZOX с учета статистического размытия по Н составляющей.
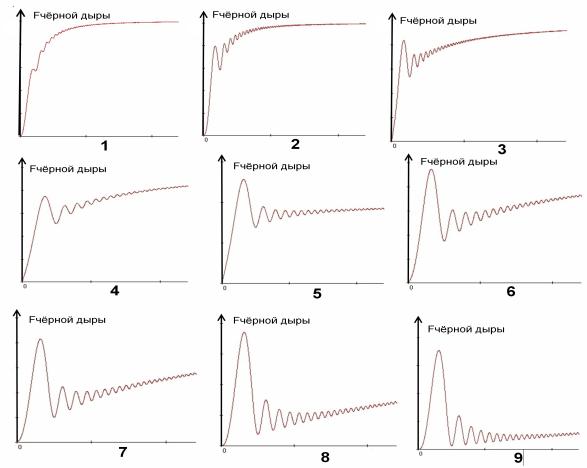
Рис.7. Графики
суммарной плоской гравитации чёрной дыры
при М→М чёрной дыры
В полярных координатах эти графики будут выглядеть,
как показано на рис.8.
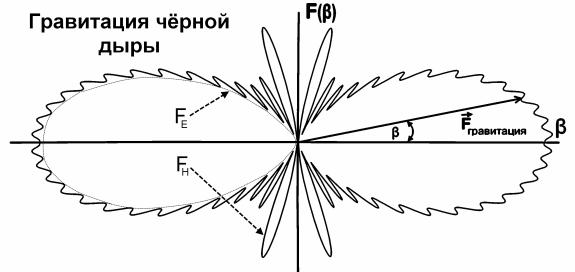
Рис.8 Гравитация чёрной дыры в полярных координатах при
М→М чёрной дыры
Поэтому при схлопывании (взрыве) звезды, взрыв будет
идти по путь наименьшего сопротивления гравитации как показано на рис.9 и будет
иметь вид конусных юбочек рис.10. По виду взрыва можно судить о степени сжатия
чёрной дыры образовавшейся в результате схлопывания звезды.
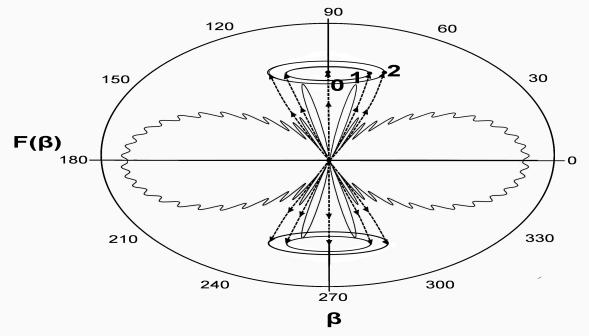
Рис.9 Гравитация
чёрной дыры в полярных координатах при
М→М чёрной дыры
с выделением конусных направлений минимальной силы F(β).
а)
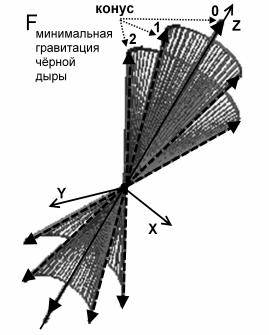
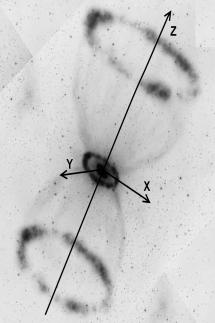
б) в)
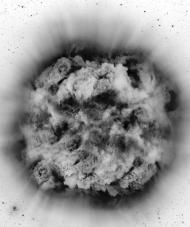
Рис.10 Изображения
взрывов звезд с формированием чёрной дыры а) Обычный сферический взрыв звезды
без формирования чёрной дыры внутри. б) График конусного взрыва при формировании
чёрной дыры. в) Взрыв звезды, где сформировалась чёрная дыра.
То есть будет отличатся от привычного сферического
взрыва из за то го, что гравитация чёрной дыры плоская.
Напомним, что гравитация и заряд рассматривается как
сумма плоских водоворотов рис.11, которые из-за статистически случайного
вращения воспринимаются как сферы. Из-за этого суммарная гравитация изменяется
пропорционально коэффициенту 1/r2 , что приводит к орбитальной скорости планет как показано на
рис.12а. При сжатии в чёрную дыру гравитация от сферической формы переходит в
плоскую рис.4-9 что приводит к распределению орбитальных скоростей в галактике
к виду показанном на рис 12.б . В нутрии галактики может быть не одна а
несколько чёрных дыр на разных стадиях сжатия, вращающихся вокруг общего
гравитационного центра, что приводит к
разнообразию форм графиков. Нестабильность (вращение) гравитационного центра
может приводить к размытию (сглаживанию) форм графиков рис.7.
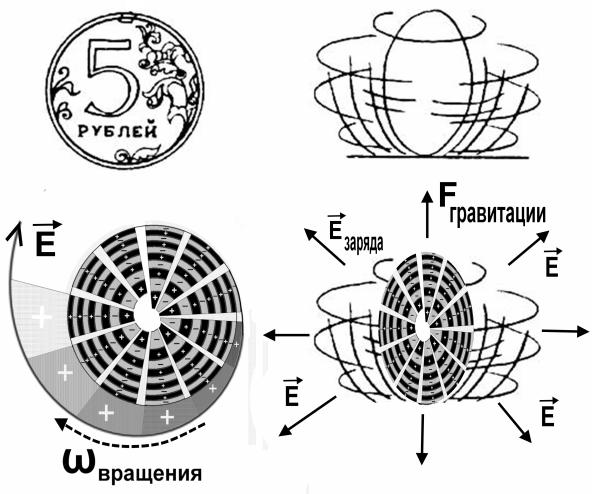
Рис.11.Водоворотная модель
частицы создающая сферический заряд и гравитацию.
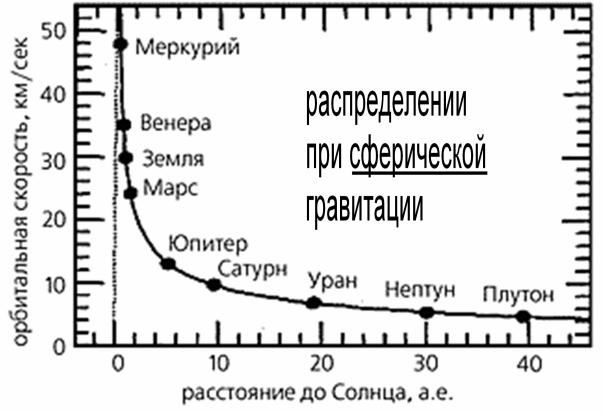
а)
б)
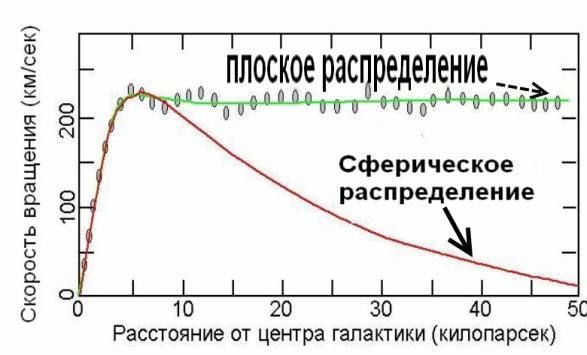
Рис.12. Распределение
орбитальных скоростей при сферическом и плоскостном распределении гравитации. а)
Сферическое распределение гравитации. б) Обобщёно разница между сферической и
плоскостной гравитацией показана
В плоскостной гравитации продольная составляющая в
основном формируется FE гравитацией, а поперечная
(колебания) формируется FH
составляющей. Гравитация рассматривается как изменяющая плотность эфира
(крептона) и базируется на схожести процессов рис.13 и рис.14;(а,б,в,). Волна в
эфирной среде движется по пути наименьшего сопротивления, наименьшей плотности эфира
рис.14.в.
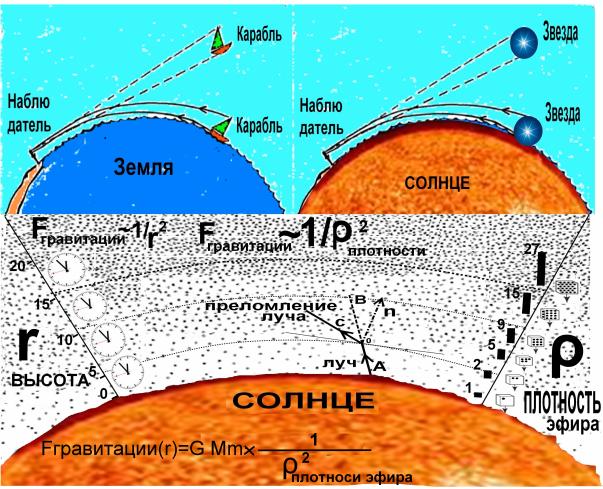
.Рис.13.Изменение расположения
звезды в следствии изменения плотности эфира.
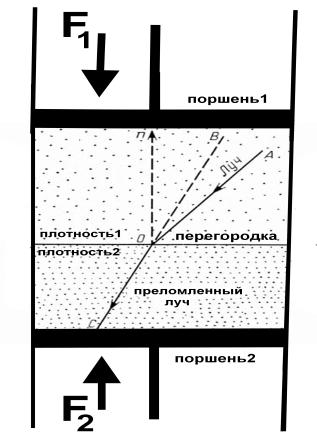
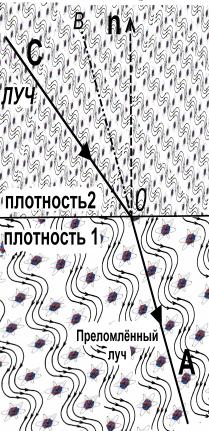
а в

г
Рис.14.Эксперемент измерения
угла преломления от ρ плотности среды.
В следствии выше изложенного уравнения гравитации
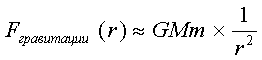 (5)
(5)
можно
переписать как:
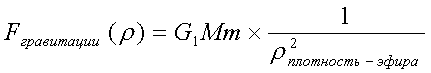 (6)
(6)
Гравитация тела оказывает воздействия на другие
объекты настолько насколько изменяет плотность эфира возле них(r (ρ плотности)). С изменением
плотности эфира меняется как было показано в предыдущих главах не только
гравитация но и время(t(ρ плотности)),
скорость света (С света(ρ плотности)), коэффициент преломления
света (n света (ρ плотности)) и другие
характеристики пространства связаны и зависят от плотности эфира.
Список литературы: 1. А. Эйнштейн. Теория относительности. 2000 Научно-издательский центр. Регулярная и хаотическая динамика. 2. Фейнман Р., Лейтон Р., Сэндс М. - Фейнмановские лекции по физике. 3. «Актуальные проблемы современных наук-2009» №.21Материалы Международной научно-практической конференции. Издат. «Nauka I studia;2009».ISBN 978-966-8736-05-6. Чёрный предел. Теория относительности: новый взгляд., Яловенко С. Н., стр. 85 4. Яловенко С. Н. Теория относительности. Новый взгляд. Яловенко С. Н. Уральский научный вестник. Научно-теоретический и практический журнал. №5(20) 2009. ЖШС «Уралнаучкнига» 2009. ISSN 1561-6908 , Теория относительности. Новый взгляд. стр. 33 5. Яловенко С. Н. Чёрный предел. Яловенко С. Н. Вестник национального технического университета "ХПИ" №8 2009г Тематический выпуск «Новые решения в современных технологиях»; Чёрный предел. Харьков, 2009 г. стр.81 6. Яловенко С. Н. Чёрный предел часть 1. Яловенко С. Н. Вестник национального технического университета "ХПИ" №43 2008г Тематический выпуск «Новые решения в современных технологиях»; Чёрный предел часть 1 Харьков, 2008 г. стр.144 7. Яловенко С. Н. «Чёрный предел. Теория относительности: новый взгляд» Яловенко С.Н. ТОВ издательство «Форт» 2009г. ISBN 978-966-8599-51-4 8. «Наука и инновации - 2010» №.13., Материалы 6 Международной научно-практической конференции.. Techniczne nauki Fizyka .издает. «Nauka I studia;2010». Яловенко С. Н. ISBN 978-966-8736-05-6. Чёрный предел. Теория относительности: новый взгляд. Часть 5. Мировоззрение, стр. 105 9. «Наука: Теория и практика - 2010» №.7.Материалы 6 Международной научно-практической конференции. издает. «Nauka I studia;2010». Яловенко С.Н., ISBN 978-966-8736-05-6. Чёрный предел. Теория относительности: новый взгляд, стр. 78 10. Yаlovenko S. N. Black limit. Theory of relativity. New view., Yаlovenko S. N. Научно-теоретический и практический журнал. «Современный научный вестник №21 (77) 2009» ISSN 1561-6886 ФИЗИКА. Стр.67. 11. «Наука: Теория и практика» №.6.., Материалы 6 Международной научно-практической конференции. издает. «Nauka I studia;2009».ISBN 978-966-8736-05-6. Yаlovenko S. N. раздел. Fizyka. Teoretyczna fizyka. Black limit. Theory of relativity. New view. Стр.17. 12. «Научный прогресс на рубеже тысячелетий - 2010»., Материалы 6 Международной научно-практической конференции. от 27.05.2010 – 05.06.2010г. издает. Прага«Education and Science». ISBN 978-966-8736-05-6. Yаlovenko S. N. Continuation of the theory of a relativity. стр. 10.
___________________________________________________________________________
АНОТАЦИЯ
Э-534
ISBN 5-93972-002-1
530.1
Ф 50
УДК
530.18 (УДК 530.10(075.4)) Яловенко С.Н. Черный предел. Часть 11. Плоский
конусный взрыв при образовании чёрной дыры. Гравитация как изменяющаяся
плотность эфира.
Вводится, новое ограничение – ни одно тело нельзя
разогнать до массы больше чем масса чёрной дыры, в дополнение по ограничению
скоростью света. На базе этого ограничения получаются новые формулы для теории
относительности и расширение классических уравнений для массы, длины, времени.
Показывается относительность заряда. Расширяются формулы для заряда и гравитации. В данной работе
рассматривается продолжение теории относительности на базе развития эфирной
теории, где дискретным элементом сверхтекучего эфира является крептон (крепкая
волна), элементарные частицы представлены плоскими водоворотами, гравитация
представлена как изменяющаяся плотность крептона (крепкая волна), создающаяся
плоскими водоворотами. Заряд представлен как растянутый водоворотом хвост
синусоиды не свёрнутый спиралью и созданный дипольным смещением крептона(эфира).
Энергия частиц представлена как превращение поступательной энергии волны во
вращательную энергию водоворота. Показано, что гравитация чёрной дыры плоская,
а не круг.
Показано что при взрыве звезды с образованием чёрной
дыры взрыв от сферического будет переходить в конусный взрыв. Уравнение
гравитации можно записать как: Fгравитация(ρплотности
эфира)=[GMm]×[1/(
ρ плотности эфира)2]×P(α , β)
Ключевые
слова: гравитация, черная дыра, водоворот,
крептон, плотность эфира, плоский конусный взрыв сверх новой звезды.
Э-534
ISBN 5-93972-002-1
530.1
Ф 50
UDK 530.18 (UDK 530.10(075.4)) Yalovenko S.N. Black limit. Part 11. Flat
cone explosion at formation of black hole. Gravitation as changing closeness of
ether.
Entered, new limitation - not a single body can not be dispersed to mass
more than mass of black hole, in addition on limiting to velocity of light. On
the base of this limitation new formulas for the theory of relativity and
expansion of classic equalizations turn out for mass, length, time. Relativity
of charge is shown. Formulas broaden for a charge and gravitation. In hired
continuation of theory of relativity is examined on the base of development of
aethereal theory, where the discrete element of сверхтекучего ether is
крептон(strong wave), elementary particles are presented by flat whirlpools, a
gravitation is presented as a changing closeness of крептона(strong wave)
created by flat whirlpools. A charge is presented however the tail of sinewave
stretched by a whirlpool is convolute a spiral and created by dipole
displacement of крептона(ether). Energy of particles is presented as converting
of forward energy of wave into rotatory energy of whirlpool. It is shown that
the gravitation of black hole is flat: Fgravitations (ρclosenesses of ether)=[GMm]×[1/( ρ closenesses of ether)2]×P(α
, β)
Keywords: gravitation, black hole, whirlpool, крептон,
closeness of ether, flat cone explosion over a new star.