Існування розв’язків задачі трансмісіі тонкої пружної
балки с в’язкопружною частиною Тимошенка та пружною частиною Кірхгофа.
Я. Бровко
ХНАДУ, вул. Петровського 25,
61002 Харків, Україна
Досліджується питання про
існування розв’язків лінійної задачі трансмісії пружної балки Кірхгофа і
в’язкопружної балки Тимошенка з нескінченним спадковим демпфуванням. Нехай тонка балка, коли
знаходиться у стані рівноваги, займає інтервал ![]() . Частина матеріалу балки, що знаходиться в інтервалі
. Частина матеріалу балки, що знаходиться в інтервалі ![]() , де
, де ![]() , має властивості Кірхгофа, тобто деформація поперечного
зсуву дуже мала. Частина балки, що знаходиться в інтервалі
, має властивості Кірхгофа, тобто деформація поперечного
зсуву дуже мала. Частина балки, що знаходиться в інтервалі ![]() , підпорядкована закону Тимошенка (див. [3]). Нехай
, підпорядкована закону Тимошенка (див. [3]). Нехай ![]() ,
, ![]() та
та ![]() . Розглядається система інтегро-диференціальних рівнянь
. Розглядається система інтегро-диференціальних рівнянь
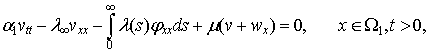 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
з граничними умовами
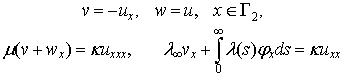 (5)
(5)
та
![]() (6)
(6)
а також початковими умовами.
Параметри ![]() є додатними
константами. Інтегральне ядро
є додатними
константами. Інтегральне ядро ![]() має властивості:
має властивості:
(K1)![]()
(K2)![]() для будь-якого
для будь-якого ![]()
(K3) існує ![]() така, що для
будь-якого
така, що для
будь-якого ![]()
![]()
Така система описує задачу
трансмісії пружних балок Тимошенка і Кірхгофа. Невідомі змінні ![]() та
та ![]() позначають
вертикальне зміщення і кут повороту поперечного перетину балки Тимошенка,
позначають
вертикальне зміщення і кут повороту поперечного перетину балки Тимошенка, ![]() - штучно введена
змінна, яка описує залежність змінної
- штучно введена
змінна, яка описує залежність змінної ![]() від попередніх станів
(см. [1]) ,
від попередніх станів
(см. [1]) ,![]() - вертикальне зміщення балки Кірхгофа. Головною ціллю даної
роботи є дослідження існування розв’язків
математичної моделі задачі.
- вертикальне зміщення балки Кірхгофа. Головною ціллю даної
роботи є дослідження існування розв’язків
математичної моделі задачі.
Введемо позначення ![]() ,
,
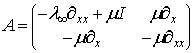 та
та 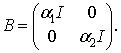
Визначимо гільбертові простори
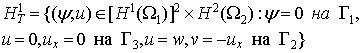
![]()
де 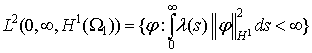 . Нехай
. Нехай
![]()
Визначимо оператор ![]()
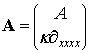
з областю визначення
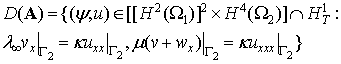
Визначимо обмежений оператор
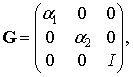
проектор
![]()
та оператор
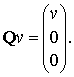
Визначимо також оператор сліду на
![]()
![]()
та оператор
![]()
Визначимо еліптичний оператор ![]() наступним чином:
наступним чином:
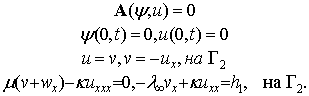
Система (1)-(6) може бути записана у вигляді
![]() (10)
(10)
![]() (11)
(11)
де
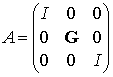
та
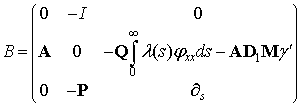
Розглянемо оператор ![]() в фазовому просторі
в фазовому просторі ![]()
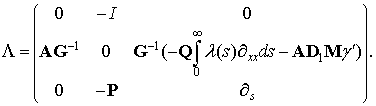
з областю визначення
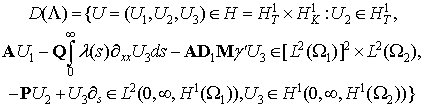
Спираючись на [2] отримуємо результат про коректну розв’язність задачі
(1) - (6):
Tеорема 1. Нехай функція ![]() задовольняє умовам
(K1)-(K3). Тоді оператор
задовольняє умовам
(K1)-(K3). Тоді оператор ![]() є генератором
стискаючої
є генератором
стискаючої ![]() - напівгрупи у
просторі
- напівгрупи у
просторі ![]() . Тобто, існує слабкий розв’язок задачі
(1) - (6) на будь-якому відрізку
. Тобто, існує слабкий розв’язок задачі
(1) - (6) на будь-якому відрізку ![]() - функція
- функція ![]() , що задовольняє
початковим умовам та співвідношенню
, що задовольняє
початковим умовам та співвідношенню ![]()
Література.
[1] Dafermos C. M. Asymptotic stability in viscoelasticity // Arch.
Rational Mech. Anal. – 1970. – Vol. 37. –
297-308.
[2] T. Fastovska On the exponential stability of Kirchhof-Timoshenko
transmission problems.// Preprint.
[3] Lagnese J. Boundary stabilization of thing plates.-Philadelphia:
SIAM, 1989. – 176 pp.