К.т.н. Калякин А.М., Сауткина Т.Н., Чеснокова Е.В., студент Линьков О.В.

Саратовский государственный университет имени Гагарина Ю.А.

ВОЛНОВОЕ СОПРОТИВЛЕНИЕ ПРЕПЯТСТВИЙ

В ОТКРЫТЫХ ПОТОКАХ

В данной статье используется метод обращения движения; его достаточно понимать в том смысле, что все параметры течения при движении тела в нём со скоростью V аналогичны параметрам потока, обтекающего со скоростью V неподвижное это же тело. Этот приём часто применяется в гидродинамике и в первом приближении дает правильные результаты.

Очевидно, что если представить движение твёрдого тела на большой глубине в идеальной жидкости (точно также как и обтекание препятствий неограниченным, в смысле глубины, потоком идеальной жидкости) результирующая сила, действующая со стороны жидкости на тело или на препятствие равна нулю. Причина этого заключается в том, что механическая энергия тела, которое движется или энергия потока, обтекающего тело в тело не переходит и не рассеивается в область вне взаимодействия.

Иной результат получается (также и в потоке идеальной жидкости) если:

- тело движется так близко к свободной поверхности, что на ней возникают гравитационные волны;

- глубина потока со свободной поверхностью такова, что вблизи препятствия образуются волны.

В перечисленных случаях волны, распространяясь, уносят с собой некоторую часть механической энергии, которая может совершать работу [3].

Например, при движении тела под свободной поверхностью (или при движении цилиндра пересекающего свободную поверхность) необходимо даже в случае если жидкость идеальная затрачивать некоторое количество энергии, которое впоследствии перейдёт в энергию волн. Величина энергии в единицу времени (мощность), требуемая для движения тела с образованием волн на поверхности может быть определена по простой зависимости

, (1)

где F – сила сопротивления, действующая на тело со стороны жидкости, V – скорость движения тела.

Сила сопротивления F, связанная исключительно с образованием волн, имеет в данном случае особый смысл – она существует и в идеальной и в реальной (вязкой) жидкости и называется волновым сопротивлением [2].

Одним из примеров того, что волны несут в себе энергию служит такой: после прохождения судна вдоль берега водоёма волны, образованные судном достигают берега и производят работу по его размыву, создают ощутимые ударные нагрузки, поднимают со дна песок и т.д.

Понятно, что эта энергия в конечном счёте получена от движения судна.

При применении метода обращения (поток обтекает препятствие) результат (1) может быть истолкована так: F – сила, действующая на неподвижный выступ в потоке, V – средняя скорость потока, Е – энергия волн.

Очевидно, что при полностью затопленном выступе (при всех остальных равных условиях) величина волнового сопротивления будет зависеть от относительной близости выступа к свободной поверхности – так как от этого зависит амплитуда (а следовательно и энергия) волн. Кроме этой геометрической величины волновое сопротивление зависит от числа Фруда.

Возникновение и поведение гравитационных волн зависит от отношения скорости потока V к скорости распространения волн С. Скорость распространения малых гравитационных волн на поверхности потока, глубина которого мала по сравнению с длиной волны определяется по формуле:

,

где g – ускорение свободного падения, h – глубина потока.

В результате получается безразмерное отношение:

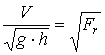, (2)

где - число Фруда.

Теоретическое решение, полученное Л. Н. Сретенский для расчета волнового сопротивления тела, движущегося в идеальной жидкости, было экспериментально проверено А.М.Калякиным для случая обтекания выступов шероховатости реальным потоком. В результате им было предложено следующее выражение для расчета коэффициента волнового сопротивления [1].

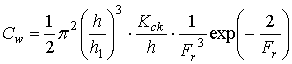, (3)

где h – глубина потока, h₁ – расстояние от свободной поверхности до середины выступа шероховатости, K_ck – высота выступа, F_r – число Фруда.

Литература

1. Богомолов А.И. и др. Высокоскоростные потоки со свободной поверхностью: Учеб. пособие для студентов вузов, обучающихся по спец. «Гидротехника» / А. И. Богомолов, В. С. Боровков, Ф. Г. Майрановский. – М.: Стройиздат, 1979. – 347 с., ил.

2. Калякин А.М. Открытые потоки: конспект лекций / А. М. Калякин. Саратов: Сарат. гос. техн. ун-т, 2006. 75с.

3. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н. Модель процесса размыва перед препятствием типа мостовой опоры. Общие закономерности вихревых образований перед обтекаемым цилиндром / Материали за 9 международна научна конференция, «Новината за напреднали наука, – 2013. Том 54. Здание и архитектура, София. «Бял ГРАД-БГ» ООД. – С. 56-59.