К.т.н., доц. Карымсаков У.Т., к.п.н., доц. Абилдабекова Д.Д., ст.преп.Иисова А.М.

Казахский Национальный технический университет им.К.И.Сатпаева

Республика Казахстан

КОНСТРУКТИВНО-МЕТРИЧЕСКИЙ СПОСОБ ПОЛУЧЕНИЯ ПРОФИЛЯ ЛОПАТОК ТУРБИН

При проектировании профилей лопаток турбин, очень важно, чтобы были обеспечены заданный поворот потока и геометрические характеристики, соответствующие заданным требованиям. Поверхности лопатки имеют сложный закон образования. Задание поверхности лопатки турбины является актуальной задачей. С учетом требований аэро- гидродинамики поперечные сечения лопаток должны быть заданы в виде обвода 2-го порядка.

Для конструирования гидродинамичной формы лопатки турбины можно использовать графический способ реализации кругового коррелятивного преобразования с линейным изменением радиуса окружности-образа.

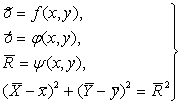(1)

где х,у – координаты точки – прообраза в плоскости;

- координаты центра окружности – образа в плоскости ;

- радиус окружности - образа в плоскости ;

, - координаты точек окружности – образа в плоскости ;

- непрерывные алгебраические функции.

При решении геометрических задач сложно использовать преобразование, задаваемое системой урвнений (1). так как, во - первых, необходимо определить постоянные коэффициенты а₁₁...а₃₃, во – вторых, необходимо постоянно вычислять . В связи с этим, требуется найти легко реализуемый графоаналитический способ задания преобразования, который бы позволил значительно упростить его использование.

Так как точки-прообразы плоскости П и центры окружностей-образов в плоскости аффинно соответственны, преобразование (1) определяется заданием трех пар соответственных точек-прообразов и окружностей-образов, при этом точки А,В,С не должны быть заданы тремя парами соответственных точек-прообразов на одной прямой и окружностей-образов, центры которых лежат на одной прямой.

Круговое коррелятивное преобразование графически заданным, если для любой точки плоскости П можно определить соответственную окружность в плоскости .

Пусть даны три точки-прообразы А(х_А,у_А), В(х_В,у_В), С(х_С,у_С), не лежащие на одной прямой в плоскости П, и соответственных им окружности-образы с радиусами в плоскости . Требуется построить окружность-образ в плоскости , соответственную точке D в плоскости П (рисунок 1).

Для решения поставленной задачи проделаем следующее:

- соединим точки А,В,С прямыми линиями;

- проведем прямую AD;

- обозначим точку пересечения прямых AD и ВС буквой К;

- согласно пятому свойству

-

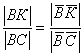
- откуда найдем положение точки :

- ;

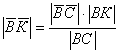- проводим касательную линию к окружностям и ;

- построим окружность касательно к ;

- определяем положение центра образа :

- ;

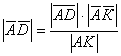- проводим касательную линию к окружностям и ;

- построим окружность касательно к прямой , что требовалось построить по условиям рассматриваемой задачи.

Теперь рассмотрим частный случай кругового коррелятивного преобразования с линейным изменением радиуса окружности-образа, когда координаты точки-прообраза равны координатам центра окружности-образа. В этом случае реализация круговое коррелятивное преобразование еще более упрощается. Система уравнений (1) примет вид

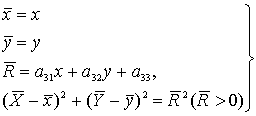(2)

Изложим графический способ задания кругового коррелятивного преобразования, определяемого системой уравнений (2). Преобразование считается заданным на чертеже, если можно построить окружность-образ, соответственную произвольной точке-прообразу, используя лишь чертежные инструменты.

Разрабатываемый графический способ основывается на свойстве кругового коррелятивного преобразования, когда прямой линии l соответствует семейство окружности ,центры которых лежат на одной прямой линии. При этом семейство имеет две касательные прямые и .

Исходя из этого свойства, если известны две окружности и , соответственные двум точкам Р и Q, лежащим на прямой l, то можно построить окружность , которая соответствует произвольной точке Т прямой l. Для этого проводим касательную к окружностям и . Затем построим искомую окружность с центром в точке Т так, чтобы она касалась прямой (рисунок 2,а).

Пусть круговое коррелятивное преобразование определено в плоскости тремя точками А,В,С, которые не принадлежат одной прямой, и соответственными им тремя окружностями с радиусами . Требуется построить окружность , соответственную точке D (рисунок 2,б). Для решения этой задачи проделаем следующее:

- через точки А и D, В и С проведем соответственно прямые линии;

- проводим касательную окружностям и ;

- построим окружность с центром в точке пересечения прямых AD и BC касательно к прямой ;

- проводим касательную прямую к окружностям и ;

- проводим искомую окружность с центром в точке D касательно к прямой , что требовалось построить по условиям рассматриваемой задачи.

Таким образом, в настоящем разделе разработан графоаналитический способ задания кругового коррелятивного преобразования, который легко реализуется с помощью линейки и циркуля, что облегчает решения некоторых теоретических и практических задач прикладной и начертательной геометрии.

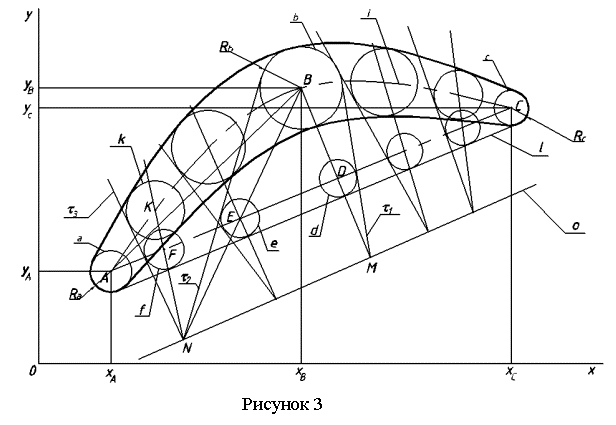
Исходными данными для конструирования профиля лопатки турбины в соответствии с рисунком 1, являются:

х_А , у_А – координаты центра дуги входной кромки;

х_В , у_В – координаты центра серединной окружности;

х_С , у_С – координаты центра дуги выходной кромки;

R_А – радиус дуги входной кромки;

R_В – радиус серединной окружности;

R_С – радиус дуги выходной кромки;

i – ось сечения лопатки.

Алгоритм построения обвода лопатки турбины имеет вид:

1. проводим прямую АС ;

2. проводим касательно к окружностям а и с прямую l.

3. на прямой АС выбираем произвольные точки D и E;

4. с центром в точке D строим касательно прямой l окружность d;

5. с центром в точке E строим касательно прямой l окружность e;

6. проводим прямую t₁ касательно окружностям b и d;

7. проводим прямую t₂ касательно окружностям b и e;

8. на пересечении прямых BD и t₁ находим точку М;

9. на пересечении прямых BЕ и t₂ находим точку N;

10. прямая О, проведенная через точки M и N является граничной линией в заданном круговом коррелятивном преобразовании;

11. на прямой АС произвольно выбираем точку F;

12. проводим прямую через точки F и N;

13. с центром в точке F строим окружность f касательно прямой l;

14. из точки N проводим прямую t₃ касательно окружности f ;

15. на пересечении прямой FN с осью лопатки получаем точку K;

16. в точке K строим окружность k касательно прямой t₃;

17. аналогично строим необходимое количество окружностей на оси i лопатки;

18. огибающая линия этого семейства окружностей будет искомой линией контура сечения лопатки.

Литература:

1. Четверухин Н.В. Проективная геометрия. М.; «Просвещение»,1969г. - 368с.

2. Иванов Г.С. Конструирование технических поверхностей.М.,1987.- 192с.

3. Геометрическое моделирование кривых линий посредством кругового коррелятивного преобразования //Поиск, №2, Алматы,2001, с.212-216.