Рахимова Г.К., Капан С.С. Lp - оценки решений одного класса вырождающихся эллиптических уравнений

 

*228387*

МАТЕМАТИКА / 3. Прикладная математика

 

К.ф.-м.н., доцент Рахимова Г.К., Капан С.С.

Таразский Государственный Университет имени М.Х.Дулати

  - оценки решений одного класса вырождающихся эллиптических уравнений

 

1.      Введение и формулировка результатов.

       Пусть  прямоугольник. Будем рассматривать в этом прямоугольнике полу периодическую задачу Дирихле:

требуется найти решения уравнения

                  ,                            (1)

удовлетворяющие условиям:

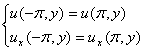                                                                                                         (2)

                                   ,                                                                           (3)

f(x,y) – заданная функция из пространства .

      Известно, что задача Дирихле для уравнения (1) со степенным вырождением, методом функции Грина изучалась в работах Геллерстедта [1] и Бицадзе [2] и получены классические решения задачи. При λ>>1 О.А.Олейником и В.А.Радкевичем [3] установлена сильная разрешимость задачи Дирихле в  для

      В случае, когда  в работе М.И.Вишика и В.В.Грушина [4] доказана разрешимость этой задачи в весовом пространстве. В работах Т.Ш.Кальменова и М.Отелбаева [5] в пространстве , рассмотрен случай, когда k(y) монотонно не убывает и удовлетворяет условию . Случай, неравномерно вырождающихся эллиптических уравнений и их коэрцитивная разрешимость в пространстве , был рассмотрен М.Б.Муратбековым [6].

В настоящей работе изучена разрешимость задачи (1)-(3) в пространстве .

      Через  обозначим класс функции сколь угодно дифференцируемых на множестве , финитных  по переменной у на [0,1] и удовлетворяющих условию (2) .

      Решением задачи (1)-(3) назовем функцию , для которой найдется последовательность , удовлетворяющая условиям :

 при .

      Теорема 1. Пусть выполнены условия:

       i) k(y)≥0 - кусочно-непрерывная функция на [0,1] и к(0)=0 ;                                     

       ii) c(y)≥δ>0 – непрерывная функция на отрезке   [0,1].

Тогда для любого, существует единственное решение задачи (1)-(3), такое, что

                                      .                                                        (4)   

 

Замечания.

1. Для оператора, определенного равенством (1) и граничными условиями Дирихле:

;

при выполнении условий i)-ii) остается справедливой теорема 1.

2.      Полученные выше результаты сохраняют силу и для задачи Дирихле в полосе

.

 

  1. Вспомогательные оценки и неравенства.

      Получим некоторые вспомогательные утверждения и оценки связанные с оператором L.

      Утверждение 2.1 Пусть выполнено условие:

      i) k(y)≥0 - кусочно-непрерывная функция на [0,1] и к(0)=0.

Тогда оператор L  положительно определён и существенно самосопряжен.

 

       Утверждение 2.2 Пусть выполнено условие:

       i) k(y)≥0 - кусочно-непрерывная функция на [0,1] и к(0)=0.

Тогда спектр оператора  L дискретен.

      Для доказательства этих утверждений сперва докажем следующие леммы.

 

      Лемма 2.1 Пусть выполнено условие i). Тогда для любого  справедлива оценка

       где с>0- постоянное число, не зависящее от u(x,y).

      Доказательство. Для  имеем:

  ;

Отсюда на основании условия i) и неравенства Коши-Буняковского имеем:

Лемма 2.1 доказана. Здесь учитывалось вещественность коэффициентов оператора L.

 

       Лемма 2.2 Пусть выполнено условие i). Тогда L симметричный оператор, т.е.

.

       Доказательство. Для  имеем:

                                                    (2.1)

Интегрируя по частям и пользуясь тем, что    находим:

.

Точно также:

.

Отсюда и из (2.1) следует, что

.

       В силу непрерывности скалярного произведения равенство  справедливо для всех . Следовательно, L симметричный оператор.

      Лемма 2.2 доказана.

 

      Лемма 2.3 Пусть выполнено условие i). Тогда  L положительно определенный оператор.

      Доказательство. Составим квадратичную форму:

.      

Интегрируя по частям и принимая во внимание граничные условия (2), (3) найдем:

.

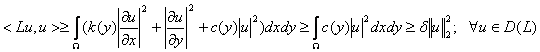Лемма 2.3 доказана.

 

       Рассмотрим оператор 

определенный первоначально на . Оператор допускает замыкание.

 

       Лемма 2.4 Пусть выполнено условие i). Тогда:

        а) для всех справедлива оценка ;

        б) оператор   существенно самосопряжен .

 

       Доказательство утверждения 2.1

       Известно, что симметричный оператор L будет существенно самосопряженным, если выполнены следующие условия:

1)      ;

2)       L  D(L)  плотно в .

Первое условие следует из леммы 2.1.

       Остается показать, что L D(L) плотно в . Отсюда будет следовать, что оператор L имеет непрерывный обратный оператор .  Это означает существование единственного сильного решения задачи (1)-(3) при всех .

      Здесь под сильным решением задачи (1)-(3) понимаем функцию , если

существует последовательность , такая что                 при .

       Теперь, после такого разъяснения вопроса, мы в дальнейшем докажем существование и единственность сильного решения задачи (1)-(3).

       Из леммы 2.4 получаем, что

                                                                                                                  (2.5)

является решением задачи (2)-(3) для уравнения

                                                              ,                                                                  (2.6)

где  ,        .

В силу леммы 2.1 имеем:

                                                                ,                                                        (2.7)

 c>0 - постоянное число.

       Так как , то из (2.7) находим, что , при . Отсюда, в силу полноты пространства  следует, что существует единственная функция  такая, что

        при .                                            (2.8) 

Из (2.6), (2.8) следует, что

.

       Последние неравенства дают, что  является решением задачи (1)-(3) при любой , а из (2.5) имеем

.

        Таким образом доказано, что множество L     D(L)  плотно в . Отсюда, из леммы 2.1-2.3 следует, что оператор L положительно определенный и существенно самосопряженный оператор.

Утверждение  2.1 доказано.

       Доказательство утверждения 2.2   

       Из леммы 2.4 следует, что  положительно определенный и самосопряженный оператор. Далее, пользуясь леммой Реллиха получаем , что спектр оператора  дискретен в том и только в том случае если множество

                                           (2.9)

компактно в . Рассмотрим множество

.

Непосредственно можно проверить, что . Так как множество  компактно в , то отсюда сразу следует, что также компактно в .

       Далее, пользуясь методом разделения переменных получаем, что, если l точка спектра оператора L, то l является точкой спектра одного из операторов

      И наоборот, если l- точка спектра одного из операторов , то l является точкой спектра оператора L. Теперь доказываемое утверждение следует из леммы Реллиха и леммы 2.4.

      При доказательстве лемм 2.5 и 2.6 мы будем пользоваться рассуждениями и выкладками работ [7-8].

 

       Лемма 2.5. Пусть выполнены условия i)-ii) Тогда для  справедлива оценка           

                                                                       (2.10)

       Доказательство. Поступим следующим образом. Пусть  и рассмотрим функционал

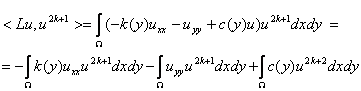                                                     (2.11)

Обозначим через  интеграл  , а через   интеграл , т.е. 

                               ,   .

       Вычислим интеграл  :

.

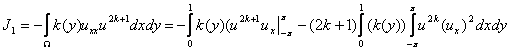Отсюда, в силу (2), имеем:

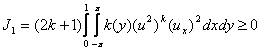                            .                                            (2.12)

Теперь рассмотрим интеграл :

.

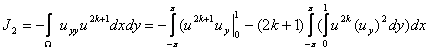Учитывая условия (3) находим:

                                 .                                                    (2.13)

Подставляя (2.12) и (2.13)  в (2.11), имеем:

.

Здесь, учитывая тот факт, что первые два интеграла неотрицательны, получаем

                  .                                (2.14)

Из (2.14)  используя неравенство Гельдера имеем:

            .

Отсюда следует неравенство (2.10). В силу непрерывности нормы неравенство (2.10) верно и для  .

      Лемма 2.5 доказана.

 

       Лемма 2.6. Пусть выполнены условия i)-ii) Тогда для  справедлива оценка           

                                                                                       (2.15)

и существует непрерывный обратный оператор.

       Доказательство леммы 2.6. Для дюбого   рассмотрим функционал:

          ,                              (2.16)

где . Обозначим через J1 интеграл , через J2 интеграл , т.е.

                               ,             

Вычислим интеграл J1 :

      (2.17)

       Далее, вычислим интеграл J2  :

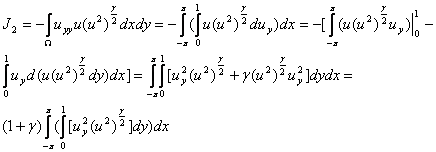                                  (2.18)

Итак, пользуясь  (2.17) и (2.18), из (2.16)  имеем:

 

.

Отсюда

.

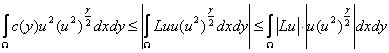Применяя последнему неравенству неравенство Гельдера и учитывая, что , находим:

или

                .                           (2.19)

Выберем  следующим образом:

.

В результате получим оценку

.

Отсюда

.

Последнее неравенство в силу непрерывности нормы справедливо для любого .

Неравенство (2.16) доказано.

      Из общей теории сопряженных операторов имеем :

                             (2.20)

где .

Известно, в случае ограниченной области, что

.

Следовательно,    Отсюда, если .

Так как, в силу утверждения, оператор L в  положительно определен и самосопряжен, поэтому . Отсюда и из (2.20) следует, что

                                              .                                                          (2.21)

Из неравенства (2.15) и из равенства (2.21) следует, что  существует непрерывный обратный оператор . Лемма 2.6 доказана.

 

       Лемма 2.7. Пусть выполнены условия i)-ii) и  пусть . Тогда справедливо равенство   

                                          ,

       где     .

       Доказательство.  Известно, и в силу леммы 2.6 существует  и

. Из общей теории линейных операторов следует, что существует ограниченный линейный оператор  и справедливо равенство

                                                  ,                                                                     (2.22)

при         .

это означает, что

                                  и     .                                               (2.23)

Мы здесь воспользовались, тем, что D(L) плотно в .

       С другой стороны, при

.

Здесь плотно в , поэтому

                                                   .                                                                 (2.24)

Равенства (2.23) и (2.24) показывают, что оператор  является обратным к , т.е. . Отсюда и из (2.22)следует, что

.

Пологая  , получим

                                                               .                                                    (2.25)

       Обозначим через ,  замыкание оператора

,

в пространстве .

 

       Лемма 2.8. Пусть выполнены условия i)-ii). Тогда для любого 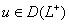 справедлива оценка

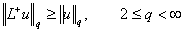                                                                           (2.26)

и оператор 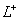 непрерывно обратим.

      Доказательство. Для удобства рассмотрим случай q=4, т.е.. Согласно (2.10), для произвольных  имеет  место

                                                          .                                                      (2.27)

Из леммы 2.7 следует, что  существует сопряженный , который непрерывно обратим  в  (- сопряженный оператор к оператору L определенного в ).

       Нетрудно установить, что . Поэтому, если докажем, что , то .

Последнее равенство доказывает  лемму 2.8 в случае q=4.

       Известно, что . Согласно леммам 2.2-2.4, оператор положительно определен и существенно самосопряжен в пространстве . Поэтому  плотно в . Пусть . Поскольку множество  плотно в , существует последовательность элементов . С другой стороны, в силу (2.27), из неравенства

следует .

       Ясно, что , покажем h=v.  Для этого рассмотрим функционал

.

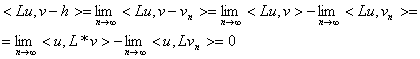Поскольку, в силу леммы 2.6,  плотно, отсюда следует v=h. Это означает . Таким образом, доказано равенство . Случай q=4 доказан. Теперь доказываемая лемма следует из леммы 2.7 и интерполяционной теоремы Рисса-Торина [9].

 

Литературы:

1.                      Gellerstedt S. Sur une equation  lineare  aux derives partielles de type mixte// Arkiv Mat. Ast. Och. Fysik – 1937.-25 A.-№29.

2.                      Бицадзе А.В. Уравнение смешанного типа. Изд. АНСССР, 1959.

3.                      Олейник О.А., Радкевич Е.В. Уравнения второго порядка с неотрицательной характеристической формой. Итоги. Наука. Математич. анализ.,1969.

4.                      Вишик М.И., Грушин В.В.// Математический сб., 79 (1), 1969 .

5.                      КальменовТ.Ш., Отелбаев М. // Дифф.ур.,-1977.-т.13.-№7.-с.1244-1255.