Экономические науки / 8. Математические методы в экономике.

Д.п.н., доцент Подповетная Ю.В., Кренев Н.В.

Финансовый университет при Правительстве Российской Федерации (Челябинский филиал), Россия

Применение математических вычислений в картографии

Одним из важных факторов успешного решения многих научных, практических и хозяйственных задач является использование карт различного назначения, содержания, масштабов и территориального охвата.

В связи с дальнейшем развитием отраслей науки, возникновением новых технических средств, таких как автоматические системы управления и навигации, появлением новых направлений науки, требующих картографо-геодезического обеспечения, как например, наук, связанных с освоением космоса, изучением и исследованиями небесных тел, более углубленным изучением Земли и ее недр, процессов и явлений природы и общества, в частности экологической обстановки в мире, разрабатываются новые типы специальных карт, создаются различные тематические карты и способы их использования.

По картам выполняются различные измерения и специальные исследования, целью которых является получение различных количественных показателей и дополнительной информации, например, для районирования (дифференциации) территорий и объектов, установления взаимосвязей, изучения динамики, определения прогнозных характеристик, выявления новых закономерностей реального мира. По картам можно решать навигационные, картометрические, морфометрические, многокомпонентные и другие задачи.

Возможность использования карт в этих и других целях основана на том, что они создаются на строгой математической основе, изучение и разработка которой является предметом математической картографии.

Математическая картография изучает и разрабатывает математическую основу карт, включающую в себя теорию картографических проекций, их применение, масштабы и компоновки, разграфки, координатные сетки и номенклатуры карт.

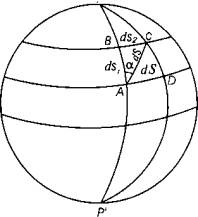
Рис. 1. Элементы сфероидической трапеции

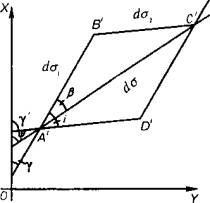
Рис.2 Элементы изображения бесконечно малой сфероидической трапеции

Рассмотрим отображение бесконечно малой сфероидической трапеции на плоскости

Бесконечно малая сфероидическая трапеция A B C D эллипсоида (рис.1) отображается на плоскость бесконечно малой косоугольной трапецией A′ B′ C′ D′ (рис.2), которую с точностью до членов более высоких порядков малости можно принять за бесконечно малый параллелограмм, а ее линейный элемент dσ=A′C′ – за бесконечно малый отрезок прямой.

Элементами этого изображения являются: безконечно малые отрезки изображения меридиана dσ₁=A′B′ и параллели dσ₂=A′D′, которые образуют с осью абсцисс Х соответственно углы γ и γ′; линейный элемент dσ, составляющий с осью Х угол ψ; азимут линейного элемента β; углы i в точках проекции между изображениями меридианов и параллелей и площадь изображения бесконечно млой сфероидической трапеции dΣ [1].

Линейный элемент

Из рис. 7 имеем:

dσ²=dx²+dy (1)

полные дифференциалы dx и dy можно представить в виде:

dx=x_φdφ+x_λλ,

dy=y_φdφ+y_λλ,

где x_φ, x_λ, y_φ, y_λ – обыкновенные или частные производные.

Подставив эти дифференциалы в выражение (1) и сгруппировав члены при одинаковых дифференциалах, получим:

dσ²=edφ² + 2fdφdλ + gdλ² (2)

где e, f, g – коэффициенты Гауса:

e=x²_φ + y²_φ; f= x_φx_λ+y_φy_λ; g=x²_λ + y²_λ. (3)

По направлениям меридианов λ = const, dλ = 0 и параллелей φ = const, и dφ = 0, следовательно, с учетом (2):

(4)

Дальнейшая разработка теории и практических вопросов математической картографии в последнее время шла по направлениям получения наилучших проекций, совершенствования проекций различных классов и характера искажений, их использование для картографирования различных территорий, разработки теории и способов выбора, изыскания проекций и автоматизации в математической картографии, способов получения проекций для создания анаморфированных карт и карт реальных поверхностей, определения математических моделей космических снимков, применения в картографии способов численного анализа и аппроксимации и т.д., а также разработки других элементов математической основы карт [2].

Литература

1. Бугаевский Л.М. Математическая картография: Учебник для вузов. – М.: 2008. - 400с.

2. Серапииас Б.Б. Математическая картография: Учебник для вузов. — М.: Издательский центр «Академия», 2005. — 336 с.