Р.Ж.Наметкулова,
А.К.Кадиримбетова, А.Абдувалов
Таразский государственный
университет имени М.Х.Дулати, Казахстан
О ВЫЧИСЛЕНИИ УСТОЙЧИВОГО НАИМЕНЬШЕГО
КВАДРАТИЧНОГО РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ФОТОМЕТРИИ
Введение. Внешняя
обратная задача потенциала Кеплера для областей с единичной плотностью сводится к решению нелинейных интегральных уравнений первого рода вида
![]() , (1)
, (1)
где ![]() - непрерывная периодическая
функция с периодом
- непрерывная периодическая
функция с периодом ![]() , описывающая известный потенциал на окружности наблюдения
, описывающая известный потенциал на окружности наблюдения ![]() с радиусом
с радиусом ![]() ,
, ![]() - неизвестная непрерывная
периодическая функция с периодом
- неизвестная непрерывная
периодическая функция с периодом ![]() , которая описывает форму
искомой области. Функции
, которая описывает форму
искомой области. Функции ![]() и
и ![]() рассматриваются как элементы функции
рассматриваются как элементы функции ![]() и
и ![]() , они состоят из множества всех вещественнозначных дважды дифференцируемых функции
, они состоят из множества всех вещественнозначных дважды дифференцируемых функции ![]() , определенных на отрезке
, определенных на отрезке ![]() и удовлетворяющих
периодическим условиям
и удовлетворяющих
периодическим условиям ![]() . В обоих пространствах норма элемента
. В обоих пространствах норма элемента ![]() определяется при
помощи
определяется при
помощи
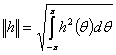 . (2)
. (2)
Вспомогательная норма определяется при помощи
![]() ,
,
где ![]() и
и ![]() являются
положительными постоянными, связанными с пространством
являются
положительными постоянными, связанными с пространством ![]() . Оператор
. Оператор ![]() является непрерывным
линейным отображением
является непрерывным
линейным отображением ![]() . Трудности в решении (1) заключаются не только в нелинейности, но и в
несуществовании обратного оператора
. Трудности в решении (1) заключаются не только в нелинейности, но и в
несуществовании обратного оператора ![]() , который даже и при
существовании часто является неограниченным.
, который даже и при
существовании часто является неограниченным.
Обратная
задача потенциала в действительности принадлежит классу некорректных задач ![]() . Несуществование
оператора
. Несуществование
оператора ![]() влечет то, что, либо
для некоторых элементов
влечет то, что, либо
для некоторых элементов ![]() уравнение (1) не
имеет решения, либо решение не является единственным.
уравнение (1) не
имеет решения, либо решение не является единственным.
Неограниченность
![]() (когда она
существует) ведет к «неустойчивости»
решения, т.е. малое возмущение
вариации нормы
(когда она
существует) ведет к «неустойчивости»
решения, т.е. малое возмущение
вариации нормы ![]() может соответствовать
большим возмущениям нормы
может соответствовать
большим возмущениям нормы ![]() .
.
На
плоскости потенциал Кеплера [2] может быть выражен в форме
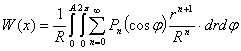 ,
,
где
![]() - полином Лежандра
- полином Лежандра ![]() - го порядка.
- го порядка.
Для
задачи, где единственность решения фиксирована, а существование и устойчивость
не фиксирована, Тихонов предложил
построить «регуляризованное» решение.
В
этой работе мы рассмотрим некоторые вычислительные аспекты применения метода
Тихонова к обратным задачам потенциала Кеплера.
Постановка
задачи. Для обратных задач
потенциала Кеплера операторное уравнение
имеет форму:
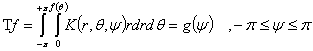 (3)
(3)
где ![]() . Предположим, что
. Предположим, что ![]() - известная функция с определенной степенью точности, т.е. вместо
- известная функция с определенной степенью точности, т.е. вместо ![]() будет
будет ![]() ,
, ![]() . Обратная задача
теории потенциалов встречается в
геофизике, астрофизике и фотометрии, где
. Обратная задача
теории потенциалов встречается в
геофизике, астрофизике и фотометрии, где ![]() может быть вполне
незначительной, поэтому ее влиянием
пренебрегают.
может быть вполне
незначительной, поэтому ее влиянием
пренебрегают.
Далее
по методу Тихонова [3], мы ищем алгоритм для вычисления приближенного решения
(3), так что это решение непрерывно зависит (по норме) от ![]() и метод заключается в
минимизации функционала
и метод заключается в
минимизации функционала
![]() , (4)
, (4)
где ![]() - параметр
регуляризации.
- параметр
регуляризации.
Тихонов
доказал, что для ![]() существует
единственная функция
существует
единственная функция ![]() , которая минимизирует функционал
, которая минимизирует функционал ![]() . Для точно выбранных
. Для точно выбранных
![]() решение вариационной
задачи становится устойчивым, т.е. для
решение вариационной
задачи становится устойчивым, т.е. для ![]() , так, что если
, так, что если
![]() , то
, то ![]() , для всех
, для всех ![]() ,
,
где ![]() и
и ![]() - минимизированные
функции соответственно
- минимизированные
функции соответственно ![]() и
и ![]() .
.
Функционал
минимизируется с помощью вариационного исчисления. Вариация ![]() на
на ![]() , где
, где ![]() - любая периодическая
функция и
- любая периодическая
функция и ![]() - малый параметр:
- малый параметр:
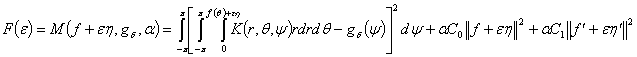 Тогда
Тогда 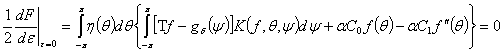 .
.
Так как это уравнение фиксировано для всех
![]() , что
, что ![]() может удовлетворять интегральное
уравнение
может удовлетворять интегральное
уравнение
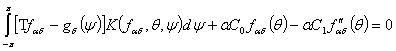 , (5)
, (5)
где граничный член появляется из
интегрирования по частям, член ![]() исчезает на основе
периодичности
исчезает на основе
периодичности ![]() и
и ![]() . Введенные индексы
. Введенные индексы ![]() указывают на то, что
решение
указывают на то, что
решение ![]() нелинейного
интегрального уравнения (5) заключается в том, что «наименьшие квадраты»
аппроксимируют решение (1), которое связано с параметром регуляризации
нелинейного
интегрального уравнения (5) заключается в том, что «наименьшие квадраты»
аппроксимируют решение (1), которое связано с параметром регуляризации ![]() и параметром
погрешности
и параметром
погрешности ![]() .
.
Для
того чтобы получить решение (5) мы дискретизируем функции. Сначала мы запишем (5): для функции ![]() заданный интервал разобьем
на
заданный интервал разобьем
на ![]() одинаковые интервалы
одинаковые интервалы ![]() , где
, где ![]() и
и ![]() . Обозначая
. Обозначая ![]() при помощи
при помощи ![]() и введя обычное
второе приращение аппроксимации
и введя обычное
второе приращение аппроксимации ![]() , мы получим
, мы получим
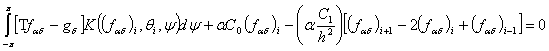 . (6)
. (6)
Член ![]() может быть выражен
численно (здесь мы пользуемся правилом Симпсона для всех численных интегралов)
и содержать все
может быть выражен
численно (здесь мы пользуемся правилом Симпсона для всех численных интегралов)
и содержать все ![]() .
.
Для
того чтобы выполнить интегрирование под ![]() , мы также дискретизируем это значение, допуская, что
, мы также дискретизируем это значение, допуская, что ![]() . Это сводится к выборочному заданию потенциала
. Это сводится к выборочному заданию потенциала ![]() этих
этих ![]() точек. В полученном
уравнении (6) интегралы будут действительными суммами при дискретизированных
переменных. Уравнение (6) будет
являться системой нелинейных алгебраических уравнений с неизвестными
точек. В полученном
уравнении (6) интегралы будут действительными суммами при дискретизированных
переменных. Уравнение (6) будет
являться системой нелинейных алгебраических уравнений с неизвестными ![]() .
.
Для выражения 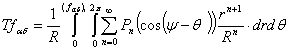 применим формулу
Симпсона и получим:
применим формулу
Симпсона и получим:
![]() ,
,
где ![]() и
и ![]() , где
, где ![]() и
и ![]() . Вводим следующее обозначение:
. Вводим следующее обозначение: 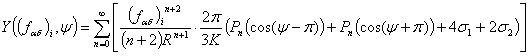 .
.
Все полученные формулы подставляем в (6) и получим:
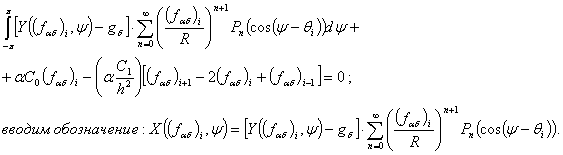
В последнем выражении для вычисления
интеграла используем формулу Симпсона и в результате получим:
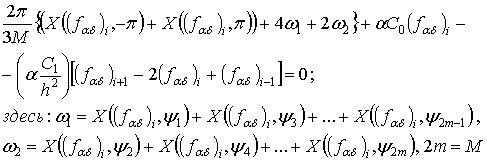
Мы решим эту систему при помощи
стандартного итеративного метода Ньютона.
В частности допустим, что
![]() ,
,
являющиеся ![]() - мерной
аппроксимацией векторного решения,
- мерной
аппроксимацией векторного решения, ![]() - является
результатом подстановки
- является
результатом подстановки ![]() в левую часть (6),
в левую часть (6), ![]() - якобиан матрицы
системы (6), выражающий
- якобиан матрицы
системы (6), выражающий ![]() . Тогда
. Тогда ![]() - итерация дается при
помощи
- итерация дается при
помощи
![]() .
.
Явная формула для элемента ![]() получается легко.
Здесь мы используем стандартный метод перестановки матрицы
получается легко.
Здесь мы используем стандартный метод перестановки матрицы ![]() .
.
Оценка погрешности. Решение ![]() в (6) зависит от
выбора параметра регуляризации и постоянных
в (6) зависит от
выбора параметра регуляризации и постоянных ![]() и
и ![]() . Если обратный оператор является неограниченным, как было
отмечено ранее выбор
. Если обратный оператор является неограниченным, как было
отмечено ранее выбор ![]() является
несущественным. С другой стороны,
является
несущественным. С другой стороны, ![]() может быть также
близко к
может быть также
близко к ![]() насколько это
возможно по норме, и это исключает
большие значения
насколько это
возможно по норме, и это исключает
большие значения ![]() . Верхняя граница
. Верхняя граница ![]() может быть получена
следующим способом.
может быть получена
следующим способом.
Пусть
![]() является регулярным
оператором, который отображает данный элемент
является регулярным
оператором, который отображает данный элемент ![]() в элемент
в элемент ![]() при помощи (5). Пусть
при помощи (5). Пусть
![]() . Пусть
. Пусть ![]() и
и ![]() являются потенциалами
соответственно
являются потенциалами
соответственно ![]() и
и ![]() , т.е. пусть
, т.е. пусть ![]() ,
, ![]() .
.
Так как ![]() минимизирует
функционалы
минимизирует
функционалы ![]() ,
,
![]() или
или
![]() .
.
Так как ![]() , то
, то
![]() . (7)
. (7)
Следовательно ![]() (8)
(8)
Из неравенства треугольника для нормы
следует:
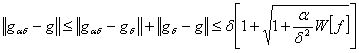 . (9)
. (9)
Уравнение (9) дает приблизительную верхнюю
грань на эффективную погрешность в ![]() , вызванную при замене
, вызванную при замене
![]() ее регулярной
аппроксимацией
ее регулярной
аппроксимацией ![]() . Для случая
. Для случая ![]() из (7) следует, что
из (7) следует, что
![]() . (10)
. (10)
Следовательно, ![]() сходится к
сходится к ![]() по норме при
по норме при ![]() . С другой стороны из (7) видно, что
. С другой стороны из (7) видно, что
![]() . (11)
. (11)
Таким образом, норма ![]() от
от ![]() является ограниченной
сверху положительной величиной.
является ограниченной
сверху положительной величиной.
Пусть ![]() является компактным
множеством всех элементов
является компактным
множеством всех элементов ![]() , которые удовлетворяют (11) и
, которые удовлетворяют (11) и ![]() является образом
отображения
является образом
отображения ![]() .
.
Впредь
отображения являются взаимно однозначными и непрерывными, обратные отображения ![]() также являются
непрерывными. Следовательно,
также являются
непрерывными. Следовательно, ![]() так, что если
так, что если
![]() , тогда
, тогда ![]() .
.
Для особых случаев, когда ![]() и
и ![]() интегральное
уравнение (5) для
интегральное
уравнение (5) для ![]() и
и ![]() пишется в таком виде:
пишется в таком виде:
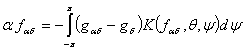 ,
,
когда ![]()
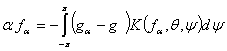 .
.
Пусть ![]() является максимальным
значением
является максимальным
значением ![]() . Подставляя его в нижние два уравнения и беря нормы (8) и
(10), учитывая в этом случае
. Подставляя его в нижние два уравнения и беря нормы (8) и
(10), учитывая в этом случае ![]() , мы находим, что
, мы находим, что 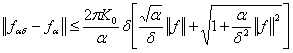 (12)
(12)
Неравенство (12) выражает верхнюю грань на ![]() для данных
для данных ![]() и
и ![]() , т.е. он выражает меру влияния погрешности в
, т.е. он выражает меру влияния погрешности в ![]() на регулярное
решение.
на регулярное
решение.
Для нахождения верхней грани ![]() для данных граней
для данных граней ![]() на
на ![]() учитывая (5) для
особого случая
учитывая (5) для
особого случая ![]() ,
, ![]() ,
, ![]() получим:
получим:
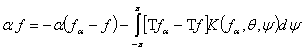 .
.
Заметим,
здесь предполагается, что решение (1) существует. Возьмем норму с обеих
сторон и получим:
![]() ,
,
где 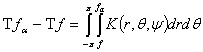 .
.
С помощью теоремы о средних значениях для
интегралов получим:
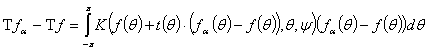 ,
,
где ![]() , следовательно
, следовательно ![]() .
.
Поэтому
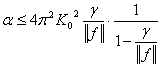 , (13)
, (13)
где ![]() .
.
Запись этого результата также требует
выпуклости ![]() , к которому может быть применена теорема о среднем значении.
Применение (13) к полученным значениям параметра регулярности требует
приблизительной априорной оценки нормы
, к которому может быть применена теорема о среднем значении.
Применение (13) к полученным значениям параметра регулярности требует
приблизительной априорной оценки нормы ![]() , а также оценки погрешности, введенной при помощи
регуляризации. В вычислительной работе
, а также оценки погрешности, введенной при помощи
регуляризации. В вычислительной работе ![]() может включать также
влияние дискретизации и округление погрешности, т.е. мы рассматриваем
может включать также
влияние дискретизации и округление погрешности, т.е. мы рассматриваем ![]() , являющийся разностью между верным решением
, являющийся разностью между верным решением ![]() и вычисленным
решением (5). Окончательно мы можем суммировать влияние регуляризации и ошибки
в
и вычисленным
решением (5). Окончательно мы можем суммировать влияние регуляризации и ошибки
в ![]() , и получить границу
на
, и получить границу
на ![]() . Из неравенства треугольников следует, что
. Из неравенства треугольников следует, что
![]() .
.
Отсюда следует, что
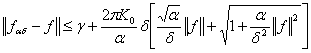 . (14)
. (14)
В заключении мы видим, что неравенство (13)
включает наибольшие значения параметра регуляризации ![]() по необходимости
связанные с большими значениями погрешности
по необходимости
связанные с большими значениями погрешности ![]() , хотя неравенство (14) показывает, что и малое
, хотя неравенство (14) показывает, что и малое ![]() может являться ошибочным. Следовательно, выбор
может являться ошибочным. Следовательно, выбор ![]() в общем виде является
критическим в вычислении разумных
аппроксимации на
в общем виде является
критическим в вычислении разумных
аппроксимации на ![]() .
.
Литература
1.
Serikbaev A. About one inverse problem of potential of simple puff for the break surface // Тезисы Международной конференции «Дифференциальные
уравнения и их приложения». Алматы, 2001, стр. 1.
2.
Наметкулова Р.Ж. Обратная задача потенциала Кеплера «в малом» // Механика и моделирование
процессов технологии. Тараз, 2007, №1, стр. 31-41
3. Тихонов А.Н. О некорректно поставленных задачах // Сб. работ ВЦ МГУ «Вычислительные методы и программирование» Вып.VIII,Изд-во МГУ, 1967.-С.3-33.