Беляева А.Ю.

Национальный технический университет Украины

«Киевский политехнический институт»

Теплофізичний розрахунок шпиндельного вузла

У сучасний час багатьом навчальним закладам достатньо тяжко купувати нові верстати, особливо, якщо цей навчальний заклад не закріплений за підприємством. Тому, я вважаю, що є необхідність у модернізації наявних верстатів. Вміння проводити теплофізичні розрахунки та експериментів є важливою кваліфікаційною характеристикою інженера машинобудівника. Це, насамперед, визначення температур у поверхневих шарах металу при обробці заготовки, оскільки температура впливає на структуру та напружений стан цих шарів, а отже, і якість готової продукції. Значну роль відігріває також вміння визначати температурну деформацію у технологічних системах, оскільки вони впливають на точність виготовлення продукції та на її взаємозамінність [1].

Диференціальне рівняння теплопровідності.

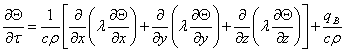(1)

де - масова теплоємність, Дж/(кг); - щільність речовини, кг/м³; , - об’ємна теплоємність рідини Дж/( м³).

Вираз (1) представляє собою диференціальне рівняння теплопровідності, що описує у самому загальному вигляді температурне поле, що виникає у твердому тілі під дією зовнішніх та внутрішніх джерел теплоти. Якщо нагрів тіла здійснюється тільки зовнішніми джерелами теплоти, то =0 та рівняння (1) спрощується. Подальше спрощення можливо отримати, якщо положити, що коефіцієнт теплопровідності не залежить від температури. У цьому випадку 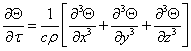(2)

де - коефіцієнт температуропровідності даної рідини, м²/с.

Коефіцієнт температуропровідності , як і коефіцієнт теплопровідності є фізичними характеристиками матеріалу[2] З формули (2) видно, що зі збільшенням швидкості зміни температури у даній точці твердого тіла [1].

Нам необхідно встановити температурне поле шпинделя токарно-револьверного металорізального верстату 1 К341 при високих швидкостях обертання шпинделя. Приймаємо наступні припущення: шпиндель представляється у вигляді стержня кінцевої довжини; підшипники служать джерелом теплотворення шпинделя з оточуючою середою здійснюється конвекцією через бокову поверхню, торцеві поверхні адіабатичні; температурне поле шпинделя одномірне та стаціонарне. 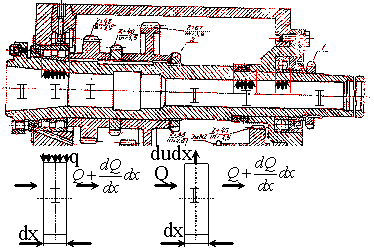З врахуванням прийнятих припущень сформована теплова модель шпинделя (рис. 1).

Для формування математичної моделі виконується розбивка шпинделя на окремі частини (рис.1), у межах яких діють джерела теплоти (частина І) та відбувається теплообмін з оточуючою середою (частина ІІ). У шпинделі виділяється елементарний об’єм у вигляді диску, товщиною та поперечним перерізом . Для виділених об’ємів складається рівняння теплового балансу, на підставі яких виводиться диференційне рівняння теплопровідності: для частини І: ; для частини ІІ: , де - інтенсивність джерела теплоутворення; - периметр шпинделя; - матеріал теплопровідності матеріалу шпинделя; - коефіцієнт тепловіддачі.

Вирішуючи диференційні рівняння аналітичним методом, отримаємо:

; (3) . (4)

Невідомі постійні величини , , , , що входять до розрахункових виразів (3)-(4) визначаються з притяганням формул для розрахунку тепловиділень у підшипниках.

Джерелом теплоутворення у підшипнику, що робить, є тертя між його деталями. Звідси, , (5)

де - сумарна потужність джерела тепловиділення, Вт; - момент тертя підшипника, Нм; - частота оберту, с^-2. , де - сила опору, що не залежить від навантаження, Н; - приведений коефіцієнт тертя шарикового радіального однорядного підшипника; - коефіцієнт пропорціональності шарикового радіального однорядного підшипника; - діаметр вала під підшипник, м; - радіальне навантаження, Н,

Рис. 1. Теплова модель шпинделя

Джерелом теплоутворення у підшипнику, що робить, є тертя між його деталями. Звідси, , (5) де - сумарна потужність джерела тепловиділення, Вт; - момент тертя підшипника, Нм; - частота оберту, с^-2. ,

де - сила опору, що не залежить від навантаження, Н; - приведений коефіцієнт тертя шарикового радіального однорядного підшипника; - коефіцієнт пропорціональності шарикового радіального однорядного підшипника; - діаметр вала під підшипник, м; - радіальне навантаження, Н,

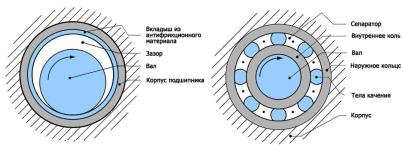
За допомогою загальної методики теплофізичного аналізу можуть бути розраховані теплові потоки та температури у підшипниках кочення. На рис. 2 показана структурна схема для підшипника кочення з тілом кочення у вигляді шарика [3].

У зв’язку з високою частотою обертання підшипника джерелом та стоки теплоти прийняті розподіленими рівномірно на робочих поверхнях зовнішнього та внутрішнього кілець та на робочій поверхні шарика. Ширина кілець, сепаратору та поверхні шарика, що торкається кільця будемо рахувати однаковими, торці кілець та поверхні шарика, що не торкаються кільця будемо рахувати адіабатичними, тобто таким, що непроникливі до теплоти.

Робочі поверхні кілець та сепаратору обмінюються теплотою з шариками. Щільність теплового потоку на поверхні шарика

(7)

; ; ; BT/м²

де - кількість шариків; - діаметр шарика.

Рис. 2. Структурна схема для підшипника кочення з тілом кочення у вигляді шарика

Середня щільність тепловиділення (6) де та діаметри поверхонь кілець, - діаметр поверхні сепаратору.

Для визначення щільності , та потоків теплообміну примінімо методику температур. Температуру на поверхні кожного з компонентів цікавлячої нас системи будемо визначати за формулами, що відносяться до півпросторів, але з поправками на круглу форму тіл. Тоді

(8); (9)

(10); (11)

де , , та - відповідно коефіцієнти форми для зовнішнього кільця, внутрішнього кільця, сепаратору та шариків. , де - радіус зовнішньої поверхні кульки

Література.

1. Резников А.Н. Теплофизика процессов механической обработки материалов.-М.: Машиностроение, 1981г., 279с., ил.

2. А.Н. Резников Тепловые процессы в технологических системах (стр. 30, 280)).

3. Якимов А.В., Слободяник П.Т.,Усов А.В. Теплофизика механической обработки. Учеб. Пособие. –К.; Одесса: Логбидь, 1991 – 240с.