Технические науки / 6.Электротехника и радиоэлектроника.

к.т.н. Черных А.Г., Сыроватский А.М.

Иркутский государственный аграрный университет, Россия

НЕСИММЕТРИЧНЫЙ РЕЖИМ ОДНОФАЗНОГО                        ЗАМЫКАНИЯ  ПРИ НЕЙТРАЛИ СЕТИ, ЗАЗЕМЛЕННОЙ                      
ЧЕРЕЗ ДУГОГАСЯЩИЙ РЕАКТОР

Согласно ПУЭ при емкостных токах замыкания на землю более 30, 20, 15, 10 А соответственно в сетях напряжением 6, 10, 15¸20, 35 кВ должна применяться компенсация тока с помощью заземляющих дугогасящих реакторов. В сетях 6¸35 кВ с ВЛ на железобетонных и металлических опорах должны использоваться дугогасящие реакторы при емкостном токе замыкания на землю более 10 А. Упрощенная схема сети заземленной через дугогасящий реактор при однофазном замыкании на землю представлена на рисунке 1.

 

 

 

 

 

 

 

 

 

 


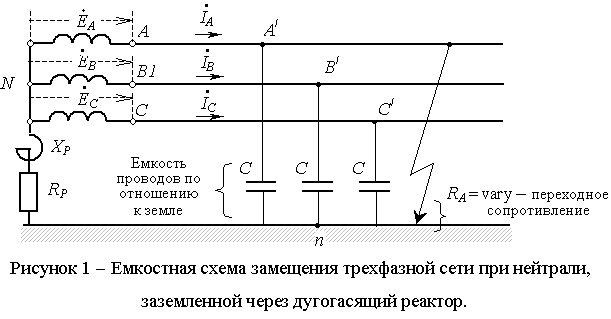
Схема замещения соответствующая данному режиму приведена на рисунке 2. В соответствии с первым законом Кирхгофа для точки (·) n             (см. рис. 2) имеем

                                                  ,    

 

где                                ;                                 ;                                ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


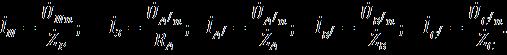
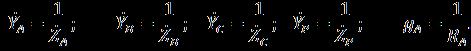
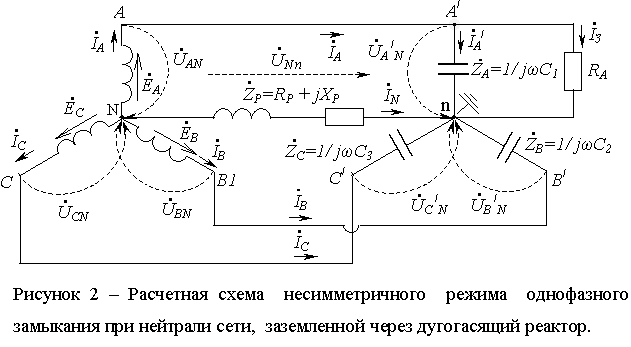
С учетом приведенных соотношений уравнение Кирхгофа примет вид:

 

       

Пусть                               а система эдс симметрична, т.е.

                           имеем:

 

 

 


Если                 т.е. равна нулю величина переходного сопротивления               

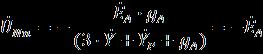
       (    , то                  

 

 

Соответственно для тока    имеем

 

и уравнение для (·) n по первому закону Кирхгофа примет вид

                                                              ,

где                                     ;                                    ;                 .

 

                                            ,  тогда

 

 


Окончательно получим:

 


Величина равная              носит название добротности реактора         , т.е.     

 Для современных реакторов величина  = 50 … 90. Как следствие, можно считать, что                .

 Пусть   , тогда

 

и ток замыкания определится выражением

                                                                                      
 

где                                   – коэффициент компенсации емкостного тока.

 

Как видно из приведенного выражения величина тока замыкания определяется действием э.д.с.    в цепи, состоящей из параллельно   соединенных емкостей всех фаз относительно земли  3С и индуктивности дугогасящего реактора  . При  К = 1 и   имеем полную компенсацию емкостного тока (резонанс токов); при   К < 1 – недокомпенсацию (емкостной ток замыкания); при К > 1 – перекомпесацию (индуктивный ток).

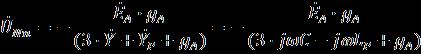Если   т.е. величина переходного сопротивления не равна нулю (, то

 

 

Определим величину   графоаналитическим способом используя следующий алгоритм:

1. Зададимся комплексной плоскостью мнимая ось которой совпадает с направлением           на соответствующей векторной диаграмме (см. рис. 3).

2. Обратим на комплексной плоскости прямую заданную уравнением:

 ,  где  ;   ;  .                                     

В качестве центра обращения  выберем (·) N векторной диаграммы.

3. Полученную в результате выполнения п.2 окружность умножим на  комплексное число:               . Определим геометрическое место точек              вектора          на комплексной плоскости.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


При выполнении геометрических построений связанных с п.1 необходимо предварительно задаться масштабом напряжений [mU] =… В/см.

 Обращение на комплексной плоскости прямой                   

выполним в два этапа.

Этап 1. Зададимся масштабом проводимости           , таким  что

 

 


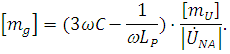
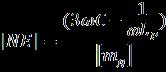По оси (+j) отложим отрезок [NE] длина которого равна

 

 

 


С  учетом  принятого масштаба            имеем                       ,   

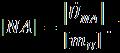где

                        

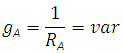
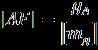
Так как по условию                      – вещественное число,   то для построения   кривой    определяющей   геометрическое место точек               (см. рис. 3), необходимо из точки   (·) E   перпендикулярно  (^)  отрезку    провести прямую. Пусть (·) F на построенной прямой и связанный  с ней отрезок            в масштабе           определяют произвольно заданное значение  такое, что

 

Из теории обращения кривых на комплексной плоскости известно, что результатом обращения прямой будет окружность. Для рассматриваемого случая (·) N – центр обращения. Прямая совпадающая с отрезком        – обращаемая прямая. В соответствии с рисунком 3 точка (·) E – обратная точка относительно центра обращения. Точка (·) L – взаимная точка относительно центра обращения. Величина определяемая произведением   равна степени обращения (S=R2). Для приведенных на рисунке 3 построений имеем:

                            ,                                   

где                      .  Тогда                                       ,  Þ                         .      

Таким образом, результатом обращения прямой  будет окружность (Nn/ E) с центром в (·) D и радиусом                                    .

Точка (·) n/ есть результат пересечения прямой |NF| и окружности с радиусом R.

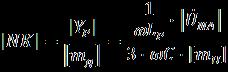
Этап 2. С учетом выбранного масштаба          по оси (–j) отложим отрезок [NK] длина которого равна

 

 

Для построений приведенных на рисунке 3 имеем

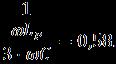       |NK| =3,5 см;  |NA| =6 см.

Следовательно,

 

По аналогии с алгоритмом построений  приведенном для 1 этапа, из точки (·) К проведем перпендикуляр (^) к отрезку [NK]. На полученной прямой  отложим     отрезок     [KВ]     такой,     что  |КВ| = |ЕF|.    Обратим     прямую

                на комплексной плоскости. При обращении учтем, что точка (·) N – центр обращения. Прямая совпадающая с отрезком [KВ] – обращаемая прямая. В соответствии с рисунком 3 точка (·) К – обратная точка. Точка (·) S – взаимная точка относительно центра обращения. Величина определяемая произведением |NS|·|NK| равна степени обращения (S=R2). Учитывая, что |NS|·|NK| = R2 (см. рис. 3),

где                                                                            

Вычислим:  |NК| = 0,58·|NА|;  |NS|·|NK| = |NS|·0,58·|NА|;  R2 = (0,29)2 · |NА|2 = =0,0841· |NА|2 , окончательно получим |NS|·0,58·|NА| = 0,0841· |NА|2  Þ

 


                                                                                           см » 0,9 см

 

Таким образом результатом обращения прямой                          будет

полуокружность (Nn// K) с центром в точке (·) Q и радиусом

R = |NQ| = 0,29·|NA| = 0,29·6 » 1,75 см.

Точка (·) n// есть результат пересечения прямой |NВ| с полуокружностью радиусом R = 1,75 см.

Геометрическая сумма векторов          и            дает вектор          .

Поворачивая данный вектор относительно центра обращения точки  (·) N до пересечения с окружностью (Nn/ E) можно получить точку (·) n. Длина вектора          дает искомое напряжение на нейтрали. Соответственно длина вектора         дает напряжение провода фазы А трехфазной линии                относительно земли.

Если              (точка (·) Р на рис. 3), то точки (·) n и (·) А/ совпадают. Следовательно,     включение     настроенного    реактора   таким  образом, что

 

 


снижает напряжение           до нуля при любом конечном значении переходного сопротивления RА.

По аналогии с правилами построений приведенными в [2], диаграмму     кривой  заданную аналитическим выражением

 

 


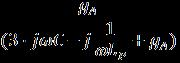
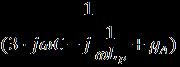можно  получить,  умножая  диаграмму (полуокружность – Nn/ EN) диаметром                                        

 

 


на вещественное число равное       

Для того, чтобы обе диаграммы изображались одной и той же кривой (окружностью), необходимо чтобы для соответствующих масштабов выполнялось равенство

                                                                        =                 ,

 


где                                             –   масштаб проводимости.

Для построения векторной диаграммы токов воспользуемся качественной диаграммой напряжений (см. рис. 3). С учетом взаимной ориентации векторов отложим вектор тока        совпадающий с вектором  напряжения         . Пусть длина         равна 4,6 см (см. рис. 4).  Выберем  произвольную  длину  вектора                

     , например - 2 см.

С   учетом   емкостного  характера       построим  вектор тока         на      векторной диаграмме рисунок 4.

Длина  вектора  напряжений            равна             = 2,9 см (см. рис. 4).

 


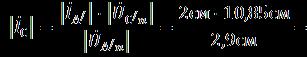
Ему соответствует вектор       длиной равной  2 см. Так как                        , то для токов       и       справедливы соотношения

 

                                или                                                                7,5 см,           

 


где              = 10,85 см (см. рис. 4). Соответственно

 


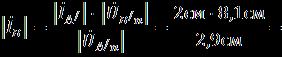
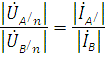
                                или                                                            5,6 см,

   

где              = 8,1 см  (см. рис. 4).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


С  учетом   емкостного  характера       и       построим соответствующие

вектора для токов      и      на диаграмме (см. рис. 4).

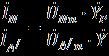
Определим величину тока       протекающего через дугогасящий реактор. Получим 

                              ,                          тогда                          ,

 

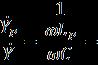
где             5,2 см (см. рис. 4),                         0,58·3 = 1,74. Соответственно

 


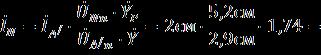
                                                                           6,24 см » 6,2 см

 


С учетом индуктивного характера                построим  вектор     тока         на диаграмме (см. рис. 4).

Для построений, приведенных на рисунке 4 справедливо соотношение

                                                  , т.е.

В целом, включение дугогасящего реактора позволяет уменьшить величину тока замыкания       . Действительно

 

 


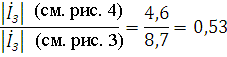
 Литература:

1. Черных А.Г.  Электротехника и основы электроники; практикум по дисциплине: учеб. пособие / А.Г. Черных.  – Иркутск:  ИрГСХА , 2010. – 272 с.

2. Черных А.Г. Несимметричный режим однофазного замыкания трехфазной электрической сети при изолированной нейтрали. / А.Г. Черных, А.М. Сыроватский, С.Ю. Сурков // Materiały X Międzynarodowej naukowi-praktycznej konferencji «Dynamika  naukowych badań - 2014» / Techniczne nauki.: Przemyśl. – Volume 8. – pp. 40-46.