Рязанов В.И., к.ф-м.н Шаповалов А.В.
Высокогорный геофизический институт, Россия, КБР,
г.Нальчик
Трехмерная численная модель распространения примесей в атмосфере с
детальным учетом метеорологических параметров
Введение. Вопросы математического моделирования распространения
загрязняющих веществ в атмосфере достаточно подробно рассмотрены в работах [1-29].
Вместе с тем, эта проблема требует дальнейшего развития, в частности, для
регионов с широким спектром местных условий, для специфических антропогенных источников
примесей. Построение математических моделей распространения атмосферных
примесей позволяет исследователям решать широкий спектр задач, в том числе,
изучать региональные и локальные особенности загрязнения окружающей среды, в
частности, атмосферного воздуха. Существует проблема построения адекватных
математических моделей, позволяющих достаточно корректно описывать
распространение примесей [1,4,7,13]. Большую сложность представляет создание
региональных моделей. Тем не менее, необходимость подобных моделей обусловлена
зачастую наличием характерных для мезорайона особенностей, которые весьма
существенны для корректных оценок. Следует отметить, что по состоянию на
текущее время, разработка моделей распространения примесей находится еще на
этапе развития.
В данной
работе представлена разработанная авторами математическая модель
распространения примесей в локальной области с учетом фактических или
прогнозных полей метеопараметров.
Тестовые расчеты
показали высокую точность расчетных схем, используемых в модели.
Для получения
прогностических полей метеорологических параметров применяются данные
Глобальной прогнозной системы (GFS). Реальные параметры
облаков и воздушных потоков в локальной области контролируются доплеровским
метеорологическим радиолокатором ДМРЛ-С.
Описание численной модели. Модель включает систему
уравнений гидротермодинамики для описания региональных атмосферных процессов,
аналогичную представленной в [1]. Для учета орографии в модели используется
обобщенная система координат 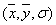 , связанная с рельефом местности
, связанная с рельефом местности
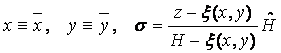 ,
(1)
,
(1)
где ![]() - высота нижней и верхней границы соответственно в z- и
- высота нижней и верхней границы соответственно в z- и ![]() - системе координат, а
- системе координат, а ![]() - функция, описывающая
рельеф [1].
- функция, описывающая
рельеф [1].
Региональная
численная модель описывает изменение со временем термодинамических и динамических
характеристик атмосферы в расчетной области.
Перенос
многокомпонентных газовых примесей рассчитывается с учетом процессов
микрофизических процессов вымывания осадками и туманами.
Основные уравнения для
скорости измерения концентрации многокомпонентных газовых примесей и аэрозолей
записываются в следующем виде [1]:
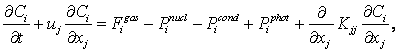 (2)
(2)
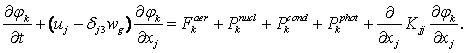 (3)
(3)
Здесь j = ![]() (u1 = u, u2
= v, u3 = w), (x1 = x, x2
= y, x3 = z); Ci, i = 1,…,Ng, jk = 1,…,Na – концентрация газовых примесей и
аэрозолей; Ng , Na - числа газовых компонент и аэрозольных фракций, соответственно; (u,v,w)- компоненты вектора скорости ветра
в направлении x,y,z, соответственно; wg- скорость гравитационного оседания; Fgas- и
Faer- источники газовых примесей и аэрозолей; Pnucl,Pcond,Pcoag и Pphot – нелинейные операторы нуклеации,
конденсации, коагуляции и фотохимической трансформации, соответственно.
(u1 = u, u2
= v, u3 = w), (x1 = x, x2
= y, x3 = z); Ci, i = 1,…,Ng, jk = 1,…,Na – концентрация газовых примесей и
аэрозолей; Ng , Na - числа газовых компонент и аэрозольных фракций, соответственно; (u,v,w)- компоненты вектора скорости ветра
в направлении x,y,z, соответственно; wg- скорость гравитационного оседания; Fgas- и
Faer- источники газовых примесей и аэрозолей; Pnucl,Pcond,Pcoag и Pphot – нелинейные операторы нуклеации,
конденсации, коагуляции и фотохимической трансформации, соответственно.
Уравнения (2)-(3) рассматриваются в области
![]()
где Н – верхняя граница области интегрирования. Начальные
условия задаются в виде:
![]() (4)
(4)
На боковых границах области задаются
следующие краевые условия:
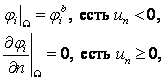 (5)
(5)
где W- боковая поверхность, n – внешняя нормаль к W, un – нормальная компонента вектора
скорости.
Уравнение турбулентной
диффузии (2)-(5) решается по методу покомпонентного расщепления [12,16].
Удаление
микропримесей газов из воздуха осуществляется за счет различных механизмов. Они
включают в себя абсорбцию и осаждение на поверхность земли, самоочищение в
процессах образования облаков и туманов, вымывание осадками и т.д. [13].
Исходной
информацией для инициализации моделей является метеорологическая информация и
данные о характеристиках источника.
Для расчета
влажного вымывания примесей атмосферными осадками в модели используются данные
радиолокационных наблюдений. С помощью метеорологических локаторов ДМРЛ-С в
аэропортах через равные промежутки времени (10 мин) строятся карты
распределения облаков и осадков на большой площади [20]. Данные об
интенсивности осадков позволяют рассчитывать поток примесей на поверхность
земли в результате вымывания.
Для анализа
полей метеорологических параметров и загрязняющих веществ авторами разработан
программный модуль трехмерного представления данных на основе современных
графических программных библиотек.
Модуль предназначен для
визуализации трехмерных наборов данных в узлах сетки, полученных в модели.
Программа позволяет строить изоповерхности, плоскости линий контура, цветные
плоскости, объемные представления данных в трехмерной сетке и т.д., затем
вращать и анимировать изображения в режиме реального времени. Реализованы также
возможности рассмотрения траектории ветра, изменение прозрачности объектов и
др. Применение средств визуализации объемных данных дает возможность их
интерпретации на высоком научном уровне.
Некоторые результаты расчетов на основе модели
Для проверки
работоспособности модели, а также алгоритмов численной реализации, проведены
тестовые расчеты, которые показали удовлетворительную точность при расчетах
распространения примесей. Задача решалась в устойчиво стратифицированной атмосфере при следующих
значениях параметров:
С0 =103
м-3; x0 = 5 км; y0 = 5 км; z0 =5 км; B =500 м; K =300 м2c-1;
w = 3 мс-1; u=v=3 мс-1.
Интегрирование системы
уравнений проводилось по пространственно-временной области ![]() . Размеры пространственной области составляли 16 км по
горизонтали и по вертикали. Шаг сетки по осям x,y,z составлял 200 м, по времени – 5 с.
. Размеры пространственной области составляли 16 км по
горизонтали и по вертикали. Шаг сетки по осям x,y,z составлял 200 м, по времени – 5 с.
В данной задаче
контрольной величиной является интегральное число частиц:
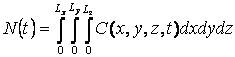 , (6)
, (6)
которое должно сохраняться при интегрировании системы по времени:
![]() . (7)
. (7)
Контрольное время t1 составляло 10 мин (600 с), время t2 составляло 20 мин (1200с). На рис.1. представлены
результаты тестовых расчетов – приведены изоповерхности концентрации примеси C = 10 м-3 в начальный момент времени t0=0 (нижняя сфера) и в момент времени t2=20 мин (верхняя сфера). Интегральное
число частиц соответственно равнялось N(0) = 10832, N(t1) = 10823,
N(t2) = 10823. Как видно, условие (7) выполняется с высокой
точностью.
Облако примеси
переносится ветром и расширяется вследствие турбулентной диффузии, максимальная
концентрация частиц со временем уменьшается. Через 5 минут она уменьшилась
примерно на порядок и составила Cmax=132,45 м-3.
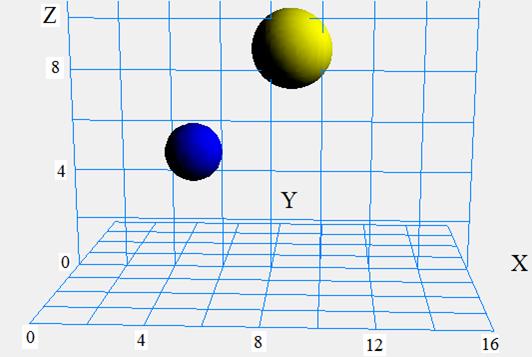
Рис.1 – Изоповерхности концентрации
частиц C = 10 м-3 в моменты времени t0=0 (нижняя сфера) и t2=20 мин (верхняя сфера).
На основе
построенной модели проведены предварительные расчеты при различных метеорологических
данных. Моделировался стационарный источник.
Была выбрана
область представляющая собой
прямоугольный пространственный параллелепипед со сторонами 16х16х10 км Ось Y
направлена на север, ось X – на восток. В области заданы метеорологические параметры
по варианту GFS [14].
Сложности
вызваны необходимостью расчета коэффициентов турбулентной диффузии в
зависимости от состояния атмосферы [7,18].
На рис.2
представлена карта горизонтального ветра по данным доплеровского
метеорологического радиолокатора ДМРЛ-С [20].
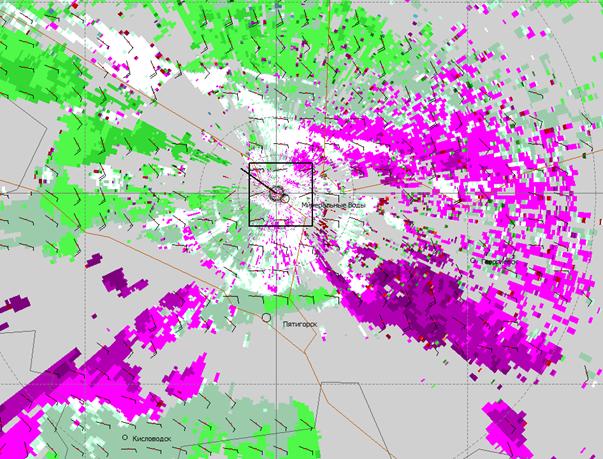
Рис. 2 -
Карта горизонтального ветра по данным ДМРЛ-С. Стрелками указано направление и
скорость ветра.
Модель позволяет по реальным данным поля ветра и облачности в
атмосфере рассчитывать распространение примесей от различных источников. Использование
данных доплеровских ДМРЛ-С значительно улучшает анализ экологической обстановки
в исследуемом районе.
Пример
расчета распространения легкой примеси представлен на рис.3. Вертикальное
распределение термодинамических параметров атмосферы и другие метеопараметры построены
по данным Глобальной системы GFS.
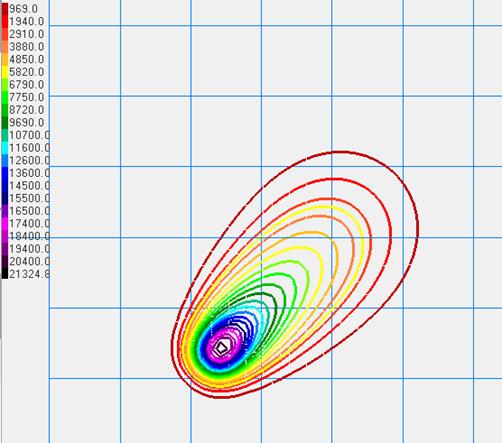
Рис.3 –
Изолинии концентрации примеси от стационарного источника в момент времени t=20
мин при К=300 м2с-1.
Заключение
Разработана математическая
модель переноса примесей в локальной области с учетом фактических или
прогнозных полей метеопараметров.
Разработаны
алгоритмы и программные модули применения данных ДМРЛ-С для построения поля
ветра в расчетной области.
При создании
информационных систем обеспечения метеорологической и экологической
безопасности жизнедеятельности людей наличие такой модели дает возможность количественного
анализа ситуации, оценки концентраций и прогноза загрязнений на фоне детальной
картины распределения метеорологических параметров.
Литература:
1. Алоян А.Е., Пененко В.В., Козодеров
В.В. Математическое моделирование в проблеме окружающей среды//в кн.
Современные проблемы вычислительной математики и математического моделирования,
т.2, Математическое моделирование. - М.: Наука, 2005. - C. 279-351.
2. Амвросов А.Ф. Особенности
распространения и рассеяния примеси над горным районом// Труды ИЭМ, 1990, вып.
51 (142).- с 45-52.
3. Аршинова В.И. и др. Некоторые данные
о загрязнении воздуха в Москве и его связи с метеорологическими условиями//
Труды ЦВГМО, Вып. 2, 1972.-С. 110-117.
4. Атмосферная турбулентность и
моделирование распространения примесей. Под редакцией Ф. Т. М. Ньюстада и Х.
Ван Допа.- Л.: Гидрометеоиздат, 1985.-351 с.
6. Безуглая Э.Ю. Метеорологический
потенциал и климатические особенности загрязнения воздуха городов. -Л.:
Гидрометеоиздат, 1980.-184 с.
7. Берлянд М.Е. Прогноз и регулирование
загрязнения атмосферы.-Л.: Гидрометеоиздат, 1985.-265 с.
8. Бызова Н.Л. Рассеяние примеси в
пограничном слое атмосферы. -М.: Гидрометеоиздат,1974.-191 с.
9. Владимиров А.М., Ляхин Ю.И., Матвеев
Л.Т., Орлов В.Т. Охрана окружающей среды.-Л.: Гидрометеоиздат, 1981.-480 с.
10.
Воробьев К.В., Постнова И.С., Широкова Л.,
Яковченко Г. Разработка информационно-моделирующей системы для оценки
загрязненности атмосферы территорий Алтайского края. Вычислительные технологии.
-2000.- Т.5.-С.117-127.
11.
Гаргер
Е.К. К оценке скорости и направления переноса примеси в пограничном слое
атмосферы//Труды ИЭМ, 1984, вып. 37 (120).- с 55-65.
12.
Дымников
В.П., Алоян А.Е. Монотонные схемы решений уравнений переноса в задачах прогноза
погоды, экологии и теории климата//ИАН. Физика атмосферы и океана, 1990, т.26,
№12.- С. 1237-1247.
13.
Израэль
Ю.А. Экология и контроль состояния природной среды.- М.: Гидрометеоиздат,
1984.-560 с.
14.
Кагермазов А.Х. Валидация выходных
данных Глобальной Системы Прогнозов GFS (Global Forecasts System) с результатами
аэрологического зондирования// Известия КБНЦ РАН. 2014. №3 (59)
– с.32-36.
15.
Кротова
И.А., Натанзон Г.А. Влияние подстилающей поверхности на распространение
невесомой примеси в приземном слое атмосферы.- Труды ИЭМ, 1978, вып. 21 (80).-
с. 45-52.
16.
Марчук
Г.И. Математическое моделирование в проблеме окружающей среды.- М.: Наука,
1982.- 319 с.
17.
Методические
указания. Регулирование выбросов при неблагоприятных метеорологических
условиях. РД 52.04.52-85. Госкомгидромет СССР, 1985.
18.
Обухов
А.М. Турбулентность и динамика атмосферы.-Л.:Гидрометеоиздат, 1988.-413 с.
19.
ОНД-86.Методика
расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в
выбросах предприятий. - Л.: Гидрометеоиздат,1987.
20.
Шаповалов А.В., Шаповалов В.А., Тапасханов
В.О., Стасенко В.Н. Программное обеспечение приема и представления информации
нового российского ДМРЛ-С// Матер. Всеросс. открытой конф. по физике облаков и
активным воздействиям на гидромет. процессы, посвященной 80-летию Эльбрусской
высокогорной комплексной экспедиции АН СССР. – Нальчик, 2014. – С.141-148.
21.
Шаповалов В.А. Численная модель
переноса и диффузии консервативной легкой примеси при заданном поле скорости
ветра// Матер. Региональной научно-практ. конф. «Проблемы информатизации
общества и образования».- Нальчик, 2004. – С.52-54.
22.
Atmospheric field experiments for evaluating
pollutant transport and dispersion in complex terrain/P.H. Gudiksen, M.H. Dickerson.
R. Lange. J.B. Knox. – In: Air Pollution Modelling and Applications. Vol. 4.
Proceedings of the 14th Int.
Techn. Meet. New York, London, 1985, p. 507-527.
23.
Atwater M.A. 1975 Thermal changes
induced by urbanization and pollutants. – J. Appl. Met., v. 14, N 16.
24.
Brown R.M., Cohen L.A., Smith M.E.
Diffusion measurements in the 10-100 km range. – Appl. Meteorol., 1972, vol.
11, N. 2, p. 323-334.
25.
Marc P., Bales C., Stanley D. A.,
Dawson G. A. Gaseous deposition to snow. Experimental Study of SO2
and NO2 deposition. J. Geophys. Res. 1987, D 82, № 8, p.p.
9779-9787.
26.
Miranda P. M, James I. N. Non-linear
three-dimensional effects on gravity-wave drag: Splitting flow and breaking
waves//Quart. J. Roy. Meteor. Soc., v.118, 1992.- P. 1057–1081.
27.
Runca E., Melli P., Spirito A. 1979
Real time forecast of sulphur dioxide
concentrations in the Venetian lagoon region. P. 1. Advection diffusion model.
IIASA, Laxenberg. 24 p.
28.
Szepesi D.J. 1978 Transmission of
sulfur dioxide on local, regional and continental scale. – Atm. Env., v. 12, N
1-3, p. 529-536.
29.
Teixeira M.A.C., Miranda P.M.A. The effect of wind shear and
curvature on gravity wave drag produced by a mountain ridge// Journal of the Atmospheric Sciences,
v.61, 2004. – P. 2638-2643.