Современные информационные технологии/2. Вычислительная техника и программирование

к.т.н. Корпань Я.В., к.т.н. Нечипоренко О.В.

Черкаський державний технологічний університет

МЕТОДИ ФІЛЬТРАЦІЇ ШУМУ ПРИ ОБРОБЦІ ЦИФРОВОГО ЗОБРАЖЕННЯ

До основних причин виникнення шумів на цифровому зображенні можна віднести два фактори: по-перше, це спотворення, які вносяться на зображення в процесі його отримання, по-друге, помилки при передачі.

Саме зображення формується різними оптико-електронними системами та фіксується за допомогою різноманітних приймачів. Таким чином, будь-який компонент пристрою може спричинити спотворення зображення. Наприклад, в процесі отримання зображення за допомогою обладнання з CCD-матрицею (або CMOS-матрицею) основним чинником, який впливає на рівень шуму, може бути рівень освітленості та температура сенсорів.

При передачі зображення шуми можуть з'явитися під впливом завад, які виникають в каналах зв'язку. Наприклад, при передачі зображення по бездротовим каналам зв'язку, воно може бути спотворене внаслідок електростатичних завад.

Найчастіше зменшення шуму служить для поліпшення візуального сприйняття, але може також використовуватися для якихось спеціалізованих цілей, наприклад, в медицині для збільшення чіткості зображення на рентгенівських знімках, як попередньої обробки для подальшого розпізнавання.

Методи обробки зображення можуть суттєво відрізнятися в залежності від того, яким шляхом зображення було отримано - синтезовано системою машинної графіки або шляхом оцифровування чорно-білої чи кольорової фотографії, відео [1].

На сьогоднішній день виділяють дві основні категорії покращення цифрового зображення та відновлення його структури:

- методи обробки в просторовій області - просторові методи;

- методи обробки в частотній області - частотні методи.

Просторові методи поліпшення зображень застосуються до растрових зображень, представлених у вигляді двовимірних матриць.

Принцип просторових алгоритмів полягає в застосуванні спеціальних операторів до кожної точки вихідного зображення. В якості операторів виступають прямокутні або квадратні матриці - маски (ядра або вікна) [2, 3]. Найчастіше маска являє собою невеликий двовимірний масив, а методи поліпшення, що базуються на такому підході, часто називають обробкою по масці або фільтрацією по масці. Її лінійним різновидом є один з варіантів двовимірної КІХ-фільтрації. В якості маски використовується множина вагових коефіцієнтів, заданих в усіх точках множини S, які симетрично оточують робочу точку кадру.

Розповсюдженим видом множини точок є квадрат 3×3 з робочим елементом в центрі. Застосовують різні види масок, одним з евристичних варіантів є рівномірна маска, усі дев'ять вагових коефіцієнтів якої дорівнюють 1/9. Такий вибір коефіцієнтів відповідає умові збереження середньої яскравості, яку можна досягти при виконанні умови

, (1)

де S - множина точок (тобто множина їх координат);

a(i₁,j₁) - вагові коефіцієнти, сукупність яких представляє собою двовимірну імпульсну характеристику.

Таким чином центрувати зображення не потрібно.

Частотні методи перетворень зображень [2, 3] ґрунтуються на ідеї перетворення Фур'є, сутність якого полягає в поданні вихідної функції у вигляді суми тригонометричних функцій різних частот, помножених на задані коефіцієнти.

У разі, якщо функція є періодичною, таке представлення називається рядом Фур'є. Інакше, неперіодична функція, що має кінцеву площу під графіком, може бути виражена у вигляді інтеграла від тригонометричних функцій, помножених на деяку вагову функцію.

Такий варіант називається перетворенням Фур'є і в більшості практичних задач виявляється більш корисним, ніж ряд Фур'є. Важливою властивістю є те, що функцію, представлену перетворенням Фур'є, після здійснення над нею перетворень можна назад повернути до початкового стану.

Таким чином, даний підхід дозволяє обробляти функцію в частотній області, після чого без втрати інформації повернутися до початкового стану. Отже перетворення Фур'є також можуть застосовуватися для вирішення завдань фільтрації зображень.

Алгоритм фільтрації зображення в частотній області складається з наступних основних кроків:

1. Початкове зображення помножується на (-1)^x+y, щоб його фур’є-перетворення було центрованим відповідно до

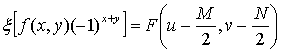, (2)

де x [∙] – перетворення Фур’є свого аргументу.

Інакше кажучи, початок координат для фур’є-перетворення функції f(x,y)(-1)^x+y (та точка, де значення цього перетворення дорівнює F(0,0)) знаходиться в точці з координатами u=M/2, v=N/2. Тобто, при множенні функції f(x,y) на величину (-1)^x+y відбувається зсув початку координат в точку з частотними координатами (M/2, N/2), яка є центром прямокутної області розміром M×N.

2. Обчислюється пряме дискретне перетворення Фур’є F(u,v) зображення.

3. Функція F(u,v) помножується на функцію фільтра Н(u,v). Функція фільтра здатна подавити деякі частоти перетворення, залишаючи інші без зміни.

4. Обчислюється зворотне дискретне перетворення Фур’є.

5. Виділяється дійсна частина результату кроку 4.

6. Результат кроку 5 помножується на (-1)^x+y.

Таким чином, швидким способом фільтрації є подавлення відповідних частот у фур'є-образі зображення, а потім зворотним перетворенням отримання відфільтрованого зображення. Подавлення відбувається шляхом поелементного множення фур'є-образа на функцію фільтра.

В деяких випадках [4] можна додатково застосовувати оптимізацію видалення шумових складових, яка полягає в локальному обчисленні вагових коефіцієнтів, які помножуються на значення шуму, яке віднімається. Найбільш відомі кругові фільтри для подавлення частот - фільтр Баттерворта, фільтр Гауса.

Ідеальний фільтр (коли просто відсікаються непотрібні частоти) викликає появу на зображенні невеликих згасаючих хвиль довкола об'єктів.

У практичному застосуванні реалізація частотних підходів може бути аналогічна просторовим методам фільтрації.

Таким чином, аналіз особливостей та принципів застосування представлених двох основних категорій методів покращення цифрового зображення показав, що просторові методи доцільно застосовувати, коли єдиним джерелом погіршення якості є білий шум, який адитивно впливає на зображення, або коли використовуються абсолютні значення яскравості пікселів (хоча може бути втрата корисної інформації, розмиття контурів) [5-7].

Частотні методи можна з певністю назвати універсальними, тому що використовуються для нечітких зображень з дефектами освітлення, також вони враховують і шуми.

Використання методів частотної фільтрації для видалення періодичних завад дозволяє видалити тільки завади (майже не зачіпаючи потрібної корисної інформації) та не вносить помітних візуальних змін. Методи частотної фільтрації можуть бути достатньо ефективно реалізовані завдяки алгоритму швидкого перетворення Фур'є.

Література:

1. Корпань Я.В. Методи та алгоритми компактного представлення графічної інформації в комп'ютерних системах [Текст]/ Я.В. Корпань // Технологічний аудит та резерви виробництва. - 2015. - Т. 3, № 2 (23). – С. 32-36. doi: 10.15587/2312-8372.2015.43330.

2. Гузман И.С. Цифровая обработка изображений в информационных системах: Учеб. пособие [Текст]/ И.С. Гузман, В.С. Киричук, В.П. Косых, Г.И. Перетягин, А.А. Спектор. - Новосибирск: Изд-во НГТУ, 2002. – 352 с.

3. Гонсалес Р. Цифровая обработка изображений. Издание 3-е, исправленное и дополненное [Текст]/ Р. Гонсалес, Р. Вудс. - Москва: Техносфера, 2012. – 1104 с.

4. Гусев В.Ю. Методика фильтрации периодических помех цифровых изображений [Электронный ресурс]/ В.Ю. Гусев, А.В. Крапивенко // Электронный журнал «Труды МАИ», 2012. - № 50. - Режим доступа: http://www.mai.ru/science/trudy/published.php?ID=28805.

5. Оппенгейм А. Цифровая обработка сигналов. 2-е издание [Текст]/ А. Оппенгейм, Р. Шафер – М.: Техносфера, 2007. – 856 с.

6. Лайонс Р. Цифровая обработка сигналов. 2-е издание [Текст]/ Р. Лайонс – М.: ООО Бином-Пресс, 2006. – 656 с.

7. Сергиенко А.Б. Цифровая обработка сигналов [Текст]/ А.Б. Сергиенко – СПб.: Питер, 2007. – 752 с.