Технические науки / 2.Механика

к.т.н. Алтухов С.В.

Иркутский государственный аграрный университет, Россия

ГРАНИЧНЫЕ УСЛОВИЯ ТЕПЛООБМЕНА РАСПЫЛИТЕЛЯ ФОРСУНКИ С ЦИЛИНДРОВЫМИ ГАЗАМИ В ДИЗЕЛЬНОМ ДВИГАТЕЛЕ 4Ч 11/12,5

Расчетно-теоретический анализ позволяет оценить тепловое состояние распылителей форсунок влияющее на их надежность и работоспособность. Метод конечных элементов (МКЭ) успешно применяется в настоящее время для решения таких задач и позволяет достичь достаточной точности расчета при условии точного и обоснованного определения граничных условий теплообмена. Граничные условия описывают тепловое взаимодействие распылителя с окружавшей средой. Различают граничные условия четырех родов [1]. Граничные условия 1-го рода задают температуру на поверхности тела (распылителя). Граничные условия 2-го рода задают тепловой поток на поверхности. Граничные условия 3-го рода задают закон теплообмена поверхности с окружающей средой, то есть температуру среды и коэффициент теплоотдачи. Граничные условия 4-го рода задаются на границе раздела двух твёрдых тел либо в виде удельного теплового потока, либо с помощью контактного термического сопротивления, величины обратной по смыслу коэффициенту теплоотдачи.

Возможны случаи, когда на отдельных участках поверхности задают граничные условия различных родов. В этом случае граничные условия будут смешанными.

На рис. 1 приведена схема распылителя с помощью, которой задаются граничные условия теплообмена.

В связи с тем, что процессы теплообмена в двигателе внутреннего сгорания (ДВС) являются периодическими, но продолжительность периода невелика а тепловая инерционность деталей камеры сгорания значительна, принято для практических расчётов теплового потока и температурного состояния деталей камеры сгорания не учитывать внутри цикловые колебания температуры [4]. В этом случае тепловое состояние деталей на установившемся режиме работы можно считать квазистационарным [4].

На поверхностях abcd и kmoprsxv (см. рис.1) задаются граничные условия 3-го рода, при этом на участке rx большую часть цикла происходит контактный теплообмен, а во время впрыскивания топлива конвективный теплообмен, поэтому граничные условия в данном случае будут смешанными. На участках dе, fg, hikl задаются граничные условия 1-го рода по экспериментально замеренным температурам.

Внешний контур распылителя включает поверхность наконечника распылителя abc и боковую поверхность распылителя cd.

На поверхности abc граничные условия 3-го рода (средний коэффициент теплоотдачи газов α_г.ср и средняя эквивалентная температура газов Т_г.экв за цикл) определяются для сравнения двумя методами. Методом термодинамической аппроксимации (ТДА) [2] и методом обработки индикаторных диаграмм, с помощью разработанной на кафедре Двигателей и теплотехники С.-Петербургского государственного аграрного университета программы НУН.

Метод ТДА позволяет получать удовлетворительные результаты для дизелей со свободным впуском. Сущность метода ТДА в том, что осреднение коэффициента теплоотдачи α_г.ср и температуры газов Т_г.экв производится на основании уравнений термодинамики [2].При этом значения α_г.ср и Т_г.экв. определяются в координатах α_г.ср-V и Т_г-Vв зависимости от объёма цилиндра.

На рис. 2 приведена диаграмма рабочего цикла дизельного двигателя.

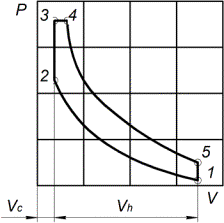
Рис. 2 Рабочий цикл дизельного двигател: V_c, V_h – объём камеры сгорания и рабочий объём, 1…5 – характерные точки диаграммы.

Средняя температура за такт сжатия определяется,

(1)

Учитывая уравнение политропы сжатия

(2)

выполняем интегрирование и после преобразования получаем,

(3)

Для такта сгорания – расширения

(4)

Используя уравнение термодинамики получим

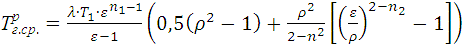(5)

В формулах (1) ¸ (5) приняты обозначения: V_h - рабочий объем цилиндра, см³; Т_г - мгновенная температура газов в цилиндре, К; V - текущий объем цилиндра, cм³; Т₁, V₁ - температура газов и объем цилиндра в начале сжатия; n₁ - показатель политропы сжатия; ε - степень сжатия; λ - степень повышения давления; ρ - степень предварительного расширения; n₂ - показатель политропы расширения.

Средняя температура газов за такт впуска [3]

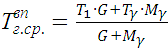(6)

где G, М_γ - масса свежего заряда и остаточных газов, кг; Т_γ - температура остаточных газов, принимается равной температуре отработавших газов, К.

Средняя температура за такт выпуска принимается равной температуре отработавших газов,

, К.

Средняя температура за цикл определяется как среднеарифметическая за такты.

Значение средней результирующей температуры по теплоотдаче
для четырёхтактных дизелей определяется [4]:

, (7)

Для определения коэффициента теплоотдачи методом ТДА использовалась формула Нусельта-Бриллинга для мгновенного коэффициента теплоотдачи, с уточнёнными коэффициентами Либровича [3] и уточнёнными коэффициентами Трактовенко [4].

, (8)

где Р_г - мгновенное давление газа в цилиндре, МПа; Т_г - мгновенная температура газа в цилиндре, К; - средняя скорость поршня, м/с; S - ход поршня, м.

Коэффициент теплоотдачи от лучеиспускания газов, Вт/(м²∙К),

, (9)

где Т_ст - температура стенок, К.

Поскольку величина теплоотдачи лучеиспусканием газов обычно не более 4…5% от общего теплового потока, нередко ею пренебрегают [4].

Формулу для определения коэффициента теплоотдачи можно представить в общем виде

,

где С - постоянная для каждой марки двигателя величина.

Тогда на такте сжатия средний коэффициент теплоотдачи,

, (10)

На такте сгорания-расширения

, (11)

После интегрирования получим

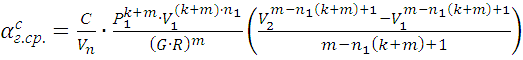, (12)

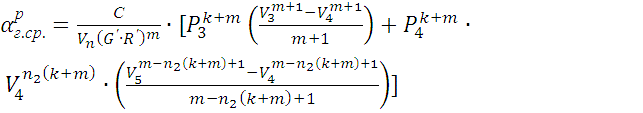, (13)

Учитывая, что k = 0,667, m = 0,333 , тогда

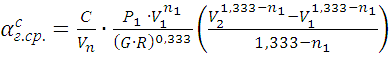, (14)

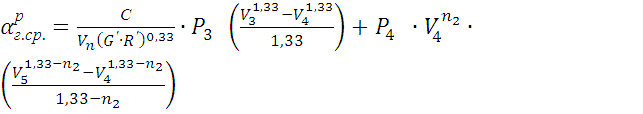, (15)

В формулах (12) ¸ (55) приняты обозначения: V₁…V₅ – объём над поршневого пространства, м³; Р₁, Р₃, Р₄ - давление газа в характерных точках, Мпа (см. рис. 2); G, G′ - масса cмеси в тактах сжатия и расширения, кг; R , R′ - газовые постоянные воздуха и смеси, Дж/(кг∙К).

Средние значения коэффициентов теплоотдачи за такты впуска и выпуска, определялись по формуле (8) с использованием результатов испытаний. При этом давление за такт впуска принималось равным Р_а, т.е. давлению в конце впуска, а в такте выпуска за расчётное принимали давление и температуру остаточных газов.

Средний коэффициент теплоотдачи за цикл подсчитывался как среднеарифметическая величина коэффициентов α_г.ср за такты.

Результаты расчёта α_г.ср и Т_гэкв методом ТДА и методом обработки индикаторных диаграмм по программе НУН с использованием формулы Вошни приведены в таблице 1.

Таблица 1

Расчётные значения средних температур и средних коэффициентов теплоотдачи от цилиндровых газов при номинальной нагрузке дизеля

№	Параметр	Такты				Среднее за цикл
		сжатие	расширение	выпуск	впуск
1	2	3	4	5	6	7
1	Тг.српо методу ТДА, Тг.экв, К	432	1380	800	370	746 1030
2	Тг.ср по индикаторной диаграмме,Тг.экв, К	426	1566	790	309	772 1072
3	αг.српо методу ТДА с формулой Нусельта-Бриллинга и коэффициентами Либровича, Вт/(м^2 ∙К)	180	442	285	121	257
4	αг.српо методу ТДА с формулой Нусельта-Бриллинга и коэффициентами Трактовенко, Вт/(м^2 ∙К)	259	650	410	173	373
5	αг.српо индикаторной диаграмме с формулой Вошни, Вт/(м^2 ∙К)	231	326	108	185	212

Из таблицы 1 видно, что значение эквивалентной температуры для обоих методов расчёта близки, расхождение составляет менее 4%. Значения среднего коэффициента теплоотдачи, полученных этими методами имеют значительный разброс. Так α_г.ср по методу ТДА с формулой Нусельта-Бриллинга и коэффициентами Либровича больше чем по индикаторной диаграмме на 21%, а по методу ТДА с формулой Нусельта-Бриллинга и коэффициентами Трактовенко больше на 76%. Результаты последующих расчётов теплового состояния распылителя при сравнении с экспериментально измеренной температурой позволят установить наиболее точный метод определения граничных условий теплообмена распылителя с цилиндровыми газами.

Величины коэффициента теплоотдачи и температуры газа по боковой поверхности cd распылителя определялись о помощью алгоритмов расчёта по программам LIТ и СЕО.

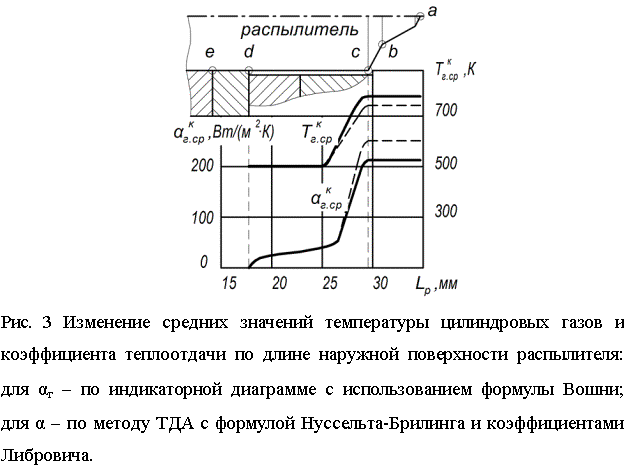Результаты определения граничных условий теплообмена по внешнему контуру распылителя представлены на рис. 3.

Анализ граничных условий позволяет сделать вывод о том, что средняя температура цилиндровых газов Т_г.ср и коэффициент теплоотдачи α_г.ср на поверхности аbс составляют: Т_г.ср = 746 К и α_г.ср = 237 Вт/(м² ∙К) для метода ТДА; Т_г.ср = 772 К и α_г.ср = 212 Вт/(м² ∙К) по значениям индикаторной диаграммы. В свою очередь, на боковой поверхности cd граничные условия уменьшаются от точки с до 2,5...3 мм от входа в кольцевой зазор головка цилиндров - распылитель и составляет Т_г.ср= 500 К, α_г.ср= 46 Вт/(м² ∙К). Далее температура газа Т_г.ср остаётся постоянной до точки d (прокладка), а коэффициент теплоотдачи постепенно уменьшается до нуля.

Литература:

1. Практикум по теплопередаче: Уч. пособие/под ред. А.П. Солодова. – М.: Энергоатомиздат, 1986. – 296 с.

2. Ждановский Н.С., Николаенко А.В. Основы и некоторые приложения термодинамической аппроксимации в расчётах ДВС / Н.С.Ждановский, А.В. Николаенко // Двигателестроение, 1981, №1. – 68 с.

3. Николаенко А.В. Теория, конструкция и расчёт автотракторных двигателей. – М.: Колос,1984. – 335 с.

4. Костин А.К. Теплонапряжённость двигателей внутреннего сгорания /А.К.Костин, В.В.Ларионов, Л.И.Михайлов. – Л.: Машиностроение, 1979. – 222 с.