к.т.н.
Бондаренко Л. Н., ст. преп. Посмитюха А.П., студ. Аблязов Р.
Днепропетровский
национальный университет железнодорожного транспорта имени академика В Лазаряна
Анализ сопротивлений
качению по выгнутой и вогнутой поверхности.
Постановка
проблемы.
Отметим, что в середине 80-х годов прошлого столетия годовое экономические
потери в США от трения, износа и разрушения контактирующих элементов машин и
иного оборудования оценивались суммой в 50 млрд. долларов [1]. Если учесть долю
США в мировой экономике, то эта цифра позволяет предположить, что каждый житель
планеты ежедневно расходует около 2,5 центов.
С учетом того, что значительная часть указанных
потерь приходится на преодолении сопротивления качению, то уменьшение последних
на транспорте, машинах и механизмах является актуальной задачей.
К сожалению, как отмечает академик К. В. Фролов,
между материаловедами и инженерами имеется совершенно необоснованное разделение
труда. Материаловед, интересуясь, в основном, свойствами материалов, редко
соотносит их с конкретными машинами. В свою очередь, инженер, обходясь
достаточно скудным сведениями, приводимыми в справочниках и не помышляющий о
том, чтобы полноправно участвовать в процессе создания конструкционных
материалов, «Однако, когда-нибудь научно-технический прогресс позволит каждой
конструкции предложить свой, соответствующий ей наилучшим образом материал [2].
Естественно, что при разработке узлов трения
качения машин необходимо иметь такие аналитические зависимости между основными
геометрическими, силовыми и механическими параметрами деталей, которым
позволили бы конструктору задаваться необходимыми и материалами еще на стадии
проектирования, а при решении оптимизационных задач варьировать не только
конструктивными параметрами, но и параметрами материалов. Естественно, что
такие зависимости не должны содержать эмпирических коэффициентов, на
определение которых требуется значительный материальные затраты и время.
Поэтому целью
статьи является получение сопротивлений качению с использованием
общепринятых механических констант материалов и геометрических размеров для
наиболее распространенных схем контакта и сравнить их по относительной величине
сопротивления качению.
Основным
материалом исследований. Сначала рассмотрим наиболее распространенные схемы
контакта.
1) Схема контакта цилиндр-плоскость
Если плоскость-рельс шириной ![]() , а цилиндр колесо радиуса
, а цилиндр колесо радиуса ![]() ,то
критическая сила при величине допускаемых контактных напряжений
,то
критическая сила при величине допускаемых контактных напряжений ![]() согласно формуле Герца [3].
согласно формуле Герца [3].
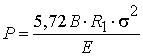 . (1)
. (1)
Данная формула справедлива для случая, когда модули
упругости колеса ![]() и рельса
и рельса ![]() одинаковы и равны
одинаковы и равны ![]() ,
а также если равны коэффициенты Пуассона
,
а также если равны коэффициенты Пуассона ![]() .
.
Полуширина полоски контакта при силе ![]()
![]() . (2)
. (2)
Значение коэффициента трения качения найдем из формулы,
полученной в [4] для крановых рельсов:
![]() . (3)
. (3)
При известных значениях ![]() и
и ![]() сопротивление качению колеса
сопротивление качению колеса
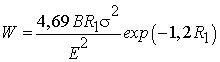 , (4)
, (4)
отметим,
что в формулах (3) и (4) радиус колеса в метрах.
Формула (4) определяет абсолютную величину сопротивления
качению. Однако, чаще всего, ввиду зависимости ![]() от
от ![]() ,
это не дает полного представления об истинном значении этого сопротивления
поэтому, введем понятие относительной величины сопротивления качению как
отношения сопротивления
,
это не дает полного представления об истинном значении этого сопротивления
поэтому, введем понятие относительной величины сопротивления качению как
отношения сопротивления ![]() к максимальной нагрузки на колесо, т.е.
к максимальной нагрузки на колесо, т.е. ![]() .
.
Это отношения имеет вид
![]() . (5)
. (5)
Зависимость ![]() от радиуса колеса
от радиуса колеса ![]() показана на рис. 1. Данные получены при
показана на рис. 1. Данные получены при ![]() МПа;
МПа; ![]() мм;
мм; ![]() МПа, а значения
МПа, а значения ![]() соответствуют допускаемым напряжениям.
соответствуют допускаемым напряжениям.
Менее важной с практической стороны, но интересно с
познавательной является величина отношения массы ![]() колеса к
колеса к ![]() ;
она показана на рис. 1.
;
она показана на рис. 1.
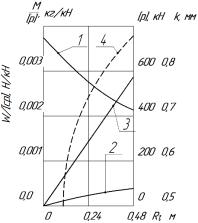
Рис. 1. Зависимости от радиуса колеса: 1
– отношения ![]() ;
;
2 – отношения ![]() ;
3 – нагрузка
;
3 – нагрузка ![]() ;
4 – коэффициента трения качения
;
4 – коэффициента трения качения ![]() .
.
Выразив ![]() через объемную массу запишем отношения
через объемную массу запишем отношения
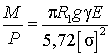 . (6)
. (6)
Приравняв правые части выражений (5) и (6), получим
уравнение, из которого может быть найден рациональный радиус колеса, при
котором его масса и сопротивление качению будут минимальны
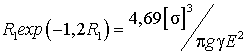 . (7)
. (7)
Для решения этого уравнения в первом приближении примем
экспоненту равной единице, т.е.
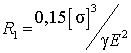 . (8)
. (8)
Во втором приближении
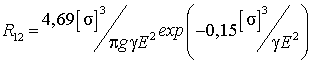 . (9)
. (9)
При ![]() т/м3 значение
т/м3 значение ![]() полученные по формуле (8) необходимо
увеличить на 10…12%, что будет соответствовать радиусу колеса
полученные по формуле (8) необходимо
увеличить на 10…12%, что будет соответствовать радиусу колеса ![]() м
м
2) Аналогичные выкладки проведём для схемы контакта
«цилиндры со взаимно перпендикулярными осями» (цилиндрическое колесо – крановый
рельс).
Как и в первом случае предположим, что модули упругости и
коэффициенты Пуассона материалов колес и рельс одинаковые.
Ввиду громоздкой зависимости между радиусам колес ![]() и радиусом закругления головки рельса
и радиусом закругления головки рельса ![]() будем поочередно принимать один из них
постоянным, а второй-изменяемым.
будем поочередно принимать один из них
постоянным, а второй-изменяемым.
В таком случаи критическую силу можно определить из формулы.
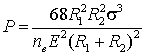 (10)
(10)
где ![]() – коэффициент, зависящий от соотношения
коэффициентов уравнения эллипса касания,
– коэффициент, зависящий от соотношения
коэффициентов уравнения эллипса касания, ![]() .
.
Полуширин пятна контакта при силе ![]()
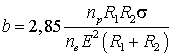 ,
(11)
,
(11)
где ![]() – коэффициент, зависящий от тех же
параметров, что и
– коэффициент, зависящий от тех же
параметров, что и ![]() .
.
Поскольку при точечном контакте [4]
![]() . (12)
. (12)
Подставив сюда значение ![]() из формулы (10), получим
из формулы (10), получим
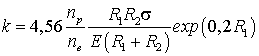 . (13)
. (13)
Сопротивление качению колеса при величине ![]() [11]
[11]
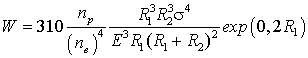 , (14)
, (14)
и
формула (4) принимает вид
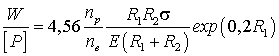 . (15)
. (15)
Отметим, что при ![]() и
и ![]() формулы (10) и (11) имеют вид.
формулы (10) и (11) имеют вид.
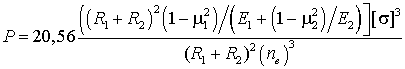 , (16)
, (16)
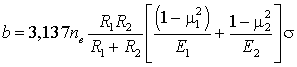 .
.
На рис. 2 показаны отношения ![]() в зависимости от закругления
в зависимости от закругления
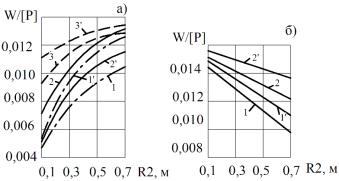
Рис. 2. Зависимость относительного сопротивления качению
колеса: а – от радиуса закругления головки рельса при различных радиусах колеса
(1, 1’ – ![]() м; 2, 2’ –
м; 2, 2’ – ![]() м; 3, 3’-
м; 3, 3’- ![]() м); б – от радиуса колеса
м); б – от радиуса колеса
(1, 1’ – ![]() ;
2, 2’ –
;
2, 2’ – ![]() м); 2’, 3’ – результаты, полученные во втором
приближении
м); 2’, 3’ – результаты, полученные во втором
приближении
головки
рельса и радиуса колеса во втором и первом приближениях. Результаты получены
при ![]() МПа.
МПа.
На рис. 3 показаны зависимости относительного сопротивления
качению колеса от допускаемых контактных напряжений.
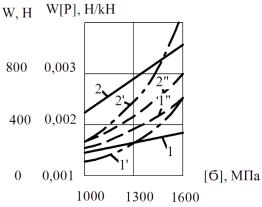
Рис. 3. Зависимость относительного
сопротивления качению колеса от допускаемых контактных напряжений (![]() мм); 1 –
мм); 1 – ![]() м;
м;
2 – ![]() м; 1’, 2’ – допускаемые нагрузки на колесо;
1”,2” – сопротивление качению колеса.
м; 1’, 2’ – допускаемые нагрузки на колесо;
1”,2” – сопротивление качению колеса.
3) Не менее важной задачей является определение
коэффициента полезного действия при передаче момента выгнутой и вогнутой поверхностями.
3.1) Цилиндры с внутренним и нагруженным
контактами.
Расчетные схемы показаны на рис. 4.
Момент необходимый для преодоления сопротивлений
только от качения при условии, что ведомым цилиндром с радиусом ![]() передается известный момент
передается известный момент ![]() .
.
Если коэффициент трения скольжения в месте
контакта ![]() ,
то необходимая сила прижатия цилиндров.
,
то необходимая сила прижатия цилиндров.
![]() . (17)
. (17)
Естественно, материал цилиндров должен быть
таким, чтоб контактные напряжения не превышали допускаемых. При тех же
допущениях, что принято выше величина ![]() найдется из выражений:
найдется из выражений:
при
наружном контакте [4]
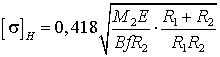 , (18)
, (18)
при
внутреннем контакте
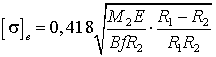 . (19)
. (19)
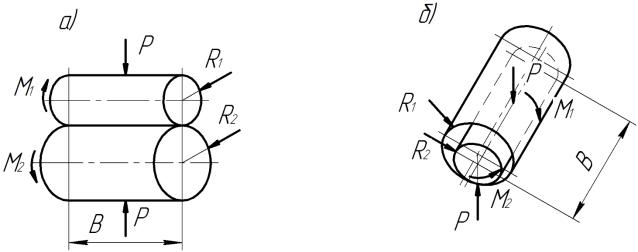
Рис. 4. Схема касания фрикционной передачи с
линейным касанием поверхностей: а) – наружное касание; б) – внутреннее касание.
Чтоб знать величину момента, необходимого для
преодоления сопротивлений качению найдем коэффициент трения качения, определив
полуширину пятна контакта:
при
нагруженном контакте
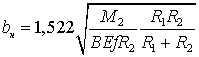 , (20)
, (20)
при
внутреннем контакте
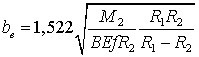 . (21)
. (21)
Коэффициент трения качения соответственно
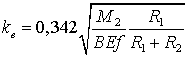 , (22)
, (22)
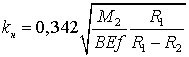 . (23)
. (23)
Момент, который необходимо преодолеть
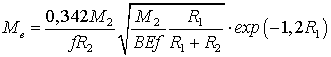 , (24)
, (24)
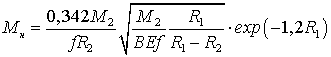 . (25)
. (25)
Отношение моментов
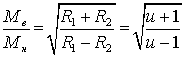 , (26)
, (26)
где ![]() – передаточное число.
– передаточное число.
Это зависимость в функции ![]() показано на рис. 5. Отметим, что и отношение
показано на рис. 5. Отметим, что и отношение ![]() имеет эту же величину (26).
имеет эту же величину (26).
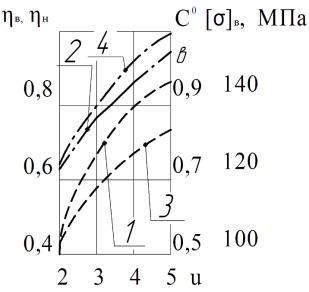
Рис. 5. Зависимость от передаточного
числа: 1 – КПД при наружном контакте; 2 – КПД при внутреннем контакте; 3 –
относительная стоимость материала при внутреннем контакте; 4 – допустимые
контактные напряжения при внутреннем контакте.
КПД передач
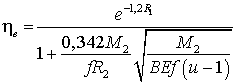 , (27)
, (27)
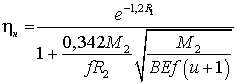 . (28)
. (28)
Зависимости ![]() и
и ![]() от передаточного числа при
от передаточного числа при ![]() Нм;
Нм; ![]()
![]() МПа;
МПа; ![]() мм;
мм; 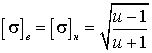 показана на рис. 5.
показана на рис. 5.
3.2 Качение по выгнутой поверхности тела вида
роликового подшипника.
В этом случаи контакт точечный и при определении
коэффициента трения качения будем пользоваться формулой (12) и для уменьшения
объёма выкладок примем модули упругости одинаковыми, а коэффициенты Пуассона
равными 0,3.
Допускаемые контактные напряжение определим из
выражений:
при выгнутом поверхности (рис.6а)
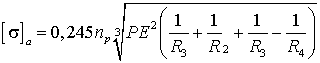 . (29)
. (29)
при вогнутый поверхности (рис. 6б)
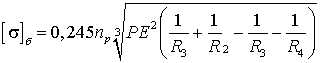 , (30)
, (30)
где ![]() – коэффициентом, зависящий от соотношения
коэффициента
– коэффициентом, зависящий от соотношения
коэффициента ![]() и
и ![]() эллипса касания.
эллипса касания.
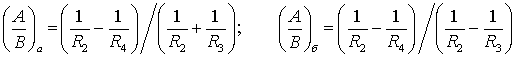 .
.
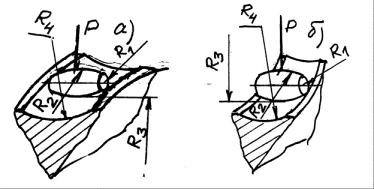
Рис. 6. Схемы касания тела качения типа
роликового подшипника:
а – выгнутая поверхность; б – вогнутая поверхность.
Чтоб размеры были одинаковыми при схемах ![]() и
и ![]() необходимо, чтоб отношении контактных
напряжений составляло
необходимо, чтоб отношении контактных
напряжений составляло
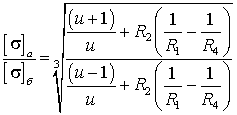 . (31)
. (31)
при одинаковых значениях ![]() и
и ![]() ,
что возможно когда
,
что возможно когда
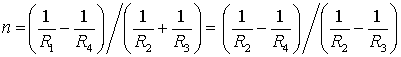 .
.
Полуширины пятин контакта
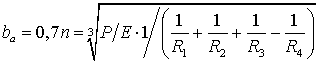 . (32)
. (32)
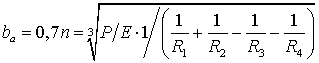 . (33)
. (33)
Соответствующие значения коэффициентов трения
качения определятся из выражений:
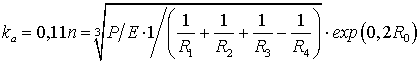 , (34)
, (34)
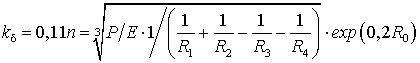 , (35)
, (35)
где ![]() – радиус качения.
– радиус качения.
Моменты необходимые для преодоления качения
роликов по поверхностям
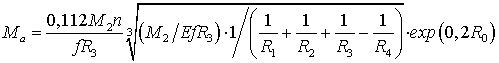 . (36)
. (36)
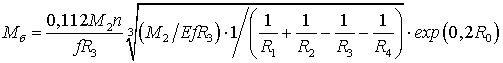 . (37)
. (37)
Аналогично (27) и (28) найдем КПД (показана на
рис. 5)
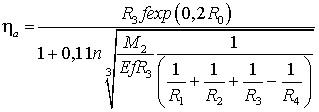 . (38)
. (38)
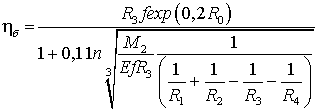 . (39)
. (39)
Анализ полученных зависимостей и графиков
позволяет сделать следующие выводы:
– предложенные формулы для определения отношения
![]() дадут возможность инженеру оперировать
геометрическими параметрами и показателями характеризующими механические
свойства тела качения и поверхности качения;
дадут возможность инженеру оперировать
геометрическими параметрами и показателями характеризующими механические
свойства тела качения и поверхности качения;
– относительное сопротивление качению колеса по
рельсу увеличивается с увеличением радиуса закругления головки рельса и
уменьшается с увеличением радиуса колеса (при нагрузке на колесо,
соответствующей величине допускаемых напряжений), а увеличение допускаемых
контактных напряжений приводит к увеличению относительной величины
сопротивления качению;
– КПД при вогнутой поверхности при качении выше,
чем выгнутой и в значительной мере зависит от соотношения радиусов.
Литература
1.
Джонсон
К. Механика контактного взаимодействия, - М.: Мир, 1989. – 510 с.
2.
Фролов
К.В. Основы НТП // Новое в жизни, науке, технике. Сер. Техника. – 1987. - № 11.
С. 8-46.
3.
Справочник
по сопротивлению материалов / Писаренко Г.С., Яковлев А.П., Матвеев В.А. –
Киев: Наук. Умка. 1988. – 736 с.
4.
Бондаренко
Л.М., Довбня М.П., Ловейкін
В.С. Деформаційні опори в машинах. Дніпропетровськ.: Дніпро-VAL, 2002. 200 c.