Муратов А., Кайнарбеков А.К., Бекмамбет К.

Алматы, Республика Казахстан

КИНЕМАТИКА ДВИЖИТЕЛЯ ДЛЯ ТРАНСПОРТНЫХ СРЕДСТВ ТИПА «ҚАҢБАҚ»

Шагающее колесо так называемый «қаңбақ» в переводе на русский язык «перекати поле» имеет простейшую конструкцию и состоит всего из двух элементов: корпуса ступицы и штанги, которые двигаются относительно друг друга при перекатывании колеса. Кинематическая модель шагающего колеса «қаңбақ» может быть представлена в виде замкнутых контуров (рисунок 1).

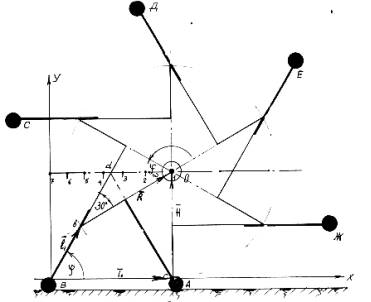
Рисунок 1. Кинематика ШК

или в скалярной форме

l₁cosf+Rcos(f-30˚) = L,

l₁sinf+Rsin(f-30˚)=H

Определим значение l₁ из второго уравнения системы

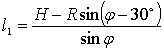
Подставив в первое уравнение системы, получим

. (1)

Эта формула показывает положение центра ступицы О в зависимости от угла поворота φ в системе координат ХВУ. Постоянные значения Н = R устанавливаются при проектировании механизма колеса. При этом необходимо учесть, что центр ступицы О движется по прямой.

Определим положение центра ступицы L₁, L₂,......L_n в зависимости от ряда значений φ_1, φ₂, φ_3,….. φ _n.

Пусть φ₁=60˚, тогда

При φ₂=70˚

При φ₃=80˚

При φ₄=90˚

При φ₅=100˚

При φ₆=110˚

При φ₇=120˚

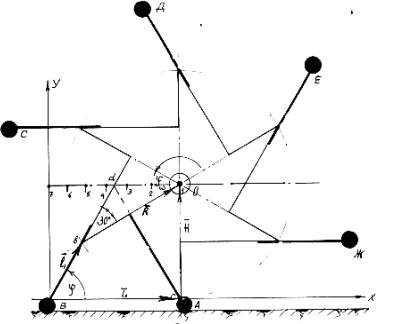
Рисунок 2. Кинематика шагающего колеса

На рисунке 2 показаны положения центра ступицы 1,2,3,4,5,6 и 7 в зависимости от угла поворота корпуса ступицы при φ₁=60˚, φ₂=70˚, φ₃=80˚, φ₄=90˚, φ₅=100˚, φ₆=110˚ и φ₇=120˚.

Следовательно, можно сделать вывод, что при равномерном вращении колеса движение центра ступицы замедляется.

Рассмотрим изменение значений V(φ) аналога скоростей в зависимости от тех же значений угла поворота φ.

Окончательно, при Н=R получим

. (2)

При φ₁=60˚,

м/рад.

При φ₂=70˚

м/рад.

При φ₃=80˚

м/рад.

При φ₄=90˚

м/рад.

При φ₅=100˚

м/рад.

При φ₆=110˚

м/рад.

При φ₇=120˚

м/рад.

Рассмотрим закон изменения ускорения центра ступицы:

.

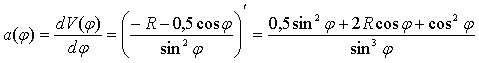При φ₁=60˚,

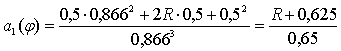м/рад∙с.

При φ₂=70˚

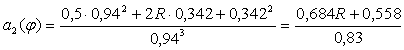м/рад∙с.

При φ₃=80˚

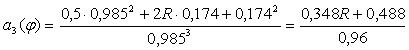м/рад∙с.

При φ₄=90˚

м/рад∙с.

При φ₅=100˚

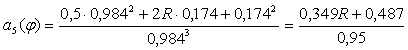м/рад∙с.

При φ₆=110˚

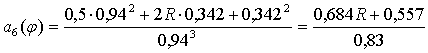м/рад∙с.

При φ₇=120˚

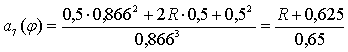м/рад∙с.

Графики полученных зависимостей L(f), V(f) и а(f) показаны на рисунке 3, из которых видно, что в конце хода (начиная с φ=90˚) ускорение а(φ) растет.

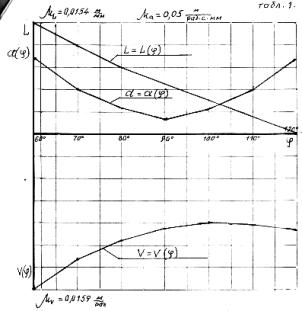
Рисунок 3. Графики изменений закона движения, скорости и ускорения

Это значит, что поступательно перемещающаяся масса экипажа с колесами развивает силу инерции, направленную прямо противоположно вектору скорости. В конце хода сила инерции за период каждого шага становится движущим фактором.

ЛИТЕРАТУРА

1. Муратов А.М., Кайнарбеков А.К. и др. Шагающие движители: Учебное пособие. «Бастау», г Алматы, 2000. 182с.

2. Муратов А.М., Кайнарбеков А.К. «Гусенично-шагающий движитель транспортного средства»: пред. патент РК №11006, г. Алматы, 14.11.2001, бюл.№12.

3. А.Кайнарбеков, А.Омаров, А.Муратов А. Хикаят шагающего колеса. «LAP» LAMBERT Academic Publishing, ,Saarbrücken, Germany, 2014.

4. Омаров А.Д., Муратов А., Кайнарбеков А., Бекмамбет К.М. «Бездорожное транспортное средства»: г. Алматы, 2015г. 182стр.