МЕТОДЫ ТЕОРИИ ИГР

ПРИ ОЦЕНКЕ ПРОИЗВОДСТВА В КОНКУРЕНТНОЙ СРЕДЕ

Маркелова И.В., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

В игре, матрица которой имеет размерность , стратегии игрока определятся наборами вероятностей , с которыми игрок применяет свои первоначальные чистые стратегии. Они будут -мерными векторами, для компонент которых справедливы условия

.

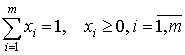Аналогично смешанными стратегиями игрока будут -мерные векторы . Для чистых стратегий справедливо

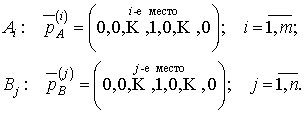
Здесь , выбираются с вероятностями, равными 1. Стратегии игроков и , для которых вероятности и отличны от нуля, будут активными.

Выигрыш игрока при использовании смешанных стратегий определится как математическое ожидание выигрыша (средняя величина)

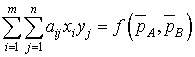
(функция - платежная функция игры с матрицей ). Стратегии , будут оптимальными, если для произвольных стратегий , выполняется условие

.

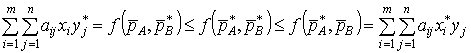При использовании в игре оптимальных смешанных стратегий выигрыш первого игрока будет, не меньший, чем при применении им любой другой стратегии ; проигрыш второго игрока будет не больше, чем при использовании им любой другой стратегии .

Решением игры будет совокупность оптимальных стратегий и цены игры. Значение платежной функции при оптимальных стратегиях определяет цену игры . Известно [1], для того, чтобы смешанные стратегии и были оптимальными, необходимо и достаточно выполнения неравенств: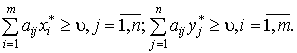

Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок (если не выходит за пределы своих активных стратегий). Решение матричной игры можно упростить, выявив при этом доминирование одних стратегий над другими: если (), то выигрыш игрока при стратегии при доминирующей будет больше, чем при доминируемой стратегии (стратегия доминирует над стратегией ). Игрок заинтересован в минимизации проигрыша; доминирующим будет столбец с наименьшими элементами. Если , то игроку свой выбор выгодно сделать по -му столбцу. В этом случае стратегия игрока доминирует над стратегией . Стратегия будет доминирующей, а стратегия – доминируемой. Если в матричной игре имеются строки (столбцы) с одними и теми же элементами, то строки (столбцы), а соответственно и стратегии игроков и , будут дублирующими. В матричной игре доминируемые и дублирующие строки (столбцы) можно опустить (не влияет на решение игры).

Ниже рассматриваются приложения метода непосредственно к планированию производства в условиях конкурентной среды.

Фирмой предполагается строительство предприятия по производству изделия в одном из регионов, затрагивая тем самым экономические интересы корпорации (объединяет фирм), производящей аналогичную продукцию. Чтобы помешать появлению конкурента, руководством корпорации используются имеющиеся в арсенале одной из своих фирм средства. В предположении, что прибыль фирмы равна потерям корпорации B, требуется указать регион для планируемого строительства предприятия фирмой .

Пусть – расчетная прибыль фирмы от реализации изделий при расположении предприятия в -м регионе и при реализации корпорацией антиконкурентных мер силами фирмы .

С целью увеличения прибыли фирма использует смешанную стратегию (случайный выбор стратегий).

Пусть для определенности определяет вероятности выбора стратегий , а набор – вероятности выбора корпорацией стратегий . Тогда прибыль фирмы при использовании смешанных стратегий будет равна

,, , .

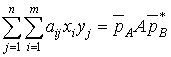Откуда прибыль равна 3,52.

Литература

1.Данилов А.М.,Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. - Пенза: ПГУАС. – 2011. – 296 с.