Математика/1.Дифференциальные и интегральные уравне­ния

 

К.ф.-м.н. Мартинюк О. В.

Чернівецький національний університет імені Юрія Федьковича,Україна

 

Розв’язність задачі Коші для еволюційних рівнянь із псевдобесселевими операторами

 

Багато різних операторів формально можна подати у вигляді , де ,  – певні інтегральні перетворення (Фур’є, Бесселя, Фур’є-Бесселя, Фур’є на півосі та ін.), визначені в тому чи іншому просторі. Значна кількість праць присвячена вивченню властивостей оператора , а також дослідженню еволюційних рівнянь з оператором  у випадку, коли , де  – перетворення Фур’є. Функція  називається символом оператора . До вказаного класу операторів належать диференціальні оператори, оператори дробового диференціювання та інтегрування, оператори згортки тощо. Властивості оператора  істотно залежать від символа цього оператора. Важливими в застосуванні (у теорії випадкових процесів, теорії фракталів) є оператори вказаного вигляду, які будуються за негладкими у точці  і однорідними за аргументом  символами: якщо символ  задовольняє ще певні умови ”параболічності”, то він називається параболічним, а еволюційні рівняння з оператором  – параболічними псевдодиференціальними рівняннями.

До класу псевдодиференціальних рівнянь природно віднести і еволюційні рівняння з операторами, побудованими за допомогою інтегральних перетворень Бесселя або Фур’є-Бесселя (так звані псевдо-Бесселеві оператори). Такі рівняння, як і рівняння з оператором Бесселя, вироджуються на межі області задання. Серед задач для еволюційних псеводиференціальних рівнянь найбільше досліджувалася задачі Коші. Для еволюційних рівнянь з псевдо-Бесселевими операторами з гладкими символами задача Коші вивчалася в роботах Я. І. Житомирського, М. І. Матійчука, С. Д. Івасишена, В. В. Крехівського, І. І. Веренич, В. В. Городецького та ін. Отримано вагомі результати стосовно коректності задачі Коші та властивостей розв’язків.

У той же час еволюційні рівняння з псевдо-Бесселевими операторами, побудованими за однорідними, негладкими у фіксованій точці символами на теперішній час досліджені не достатньо повно. У даній роботі будуються нові класи псевдодиференціальних операторів, які містять в собі клас псевдо-Бесселевих операторів, побудованих за сталими символами. Розвивається теорія задачі Коші для еволюційних рівнянь з такими операторами та початковими даними з просторів узагальнених функцій типу розподілів.

 Простори основних та узагальнених функцій. Нехай , :  – неперервні, парні на  функції, диференційовні, монотонно зростаючі й необмежені на , , причому функція  опукла (донизу) на , тобто:

а) : ;

б)  : ;

в)  : .

Припускаємо також, що виконуються наступні умови:

  : ,

, , , ,

де  та  – фіксовані параметри.

Символом  позначимо сукупність усіх неперервних, парних на  функцій : , нескінченно диференційовних на , для яких

(якщо , то сума відсутня, якщо , то  і т.д.; якщо , то вказана нерівність справджується для всіх ).

Наведемо приклад функції із простору , побудованому за конкретними функціями  та . Для цього розглянемо неперервну функцію : , однорідну порядку , парну на , нескінченно диференційовну на , похідні якої задовольняють умову:

 .

Цю умову можна подати у вигляді: , , , де , . Тоді функція  є елементом простору  із вказаними функціями  та  (функція  використовується при побудові псевдодиференціальних операторів, для яких вона є негладким у точці 0 однорідним символом [1]). Справді, скориставшись формулою Фаа де Бруно диференціювання складеної функції, можна переконатися в тому, що справджуються нерівності

де , , звідки й випливає, що  є елементом простору .

Нехай  – фіксоване число з множини . На функціях з простору  визначене перетворення Бесселя  [2]:

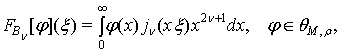
де  – нормована функція Бесселя;  – парна на  функція.

Теорема 1.  Якщо , то . Для функції  та її похідних справджуються оцінки

         

, , .

Нехай . Введемо в  структуру зліченно-нормованого простору за допомогою норм

         

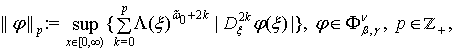
де , , ,  – фіксований параметр. Збіжність у просторі  – це збіжність за кожною нормою , . Ця збіжність еквівалентна такій: послідовність  збігається за топологією простору  до функції  тоді й лише тоді, коли вона: 1) обмежена в , тобто   : ; 2) правильно збігається в , а саме, для довільного  послідовність  збігається до нуля рівномірно на кожному відрізку .

Теорема 2.  Перетворення Бесселя неперервно відображає  на простір .

Зазначимо також, що простір  є досконалим (тобто в цьому просторі кожна обмежена множина є компактною).

Символом  позначимо оператор узагальненого зсуву аргументу, який відповідає оператору Бесселя [2]:

         

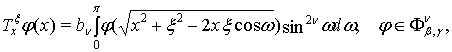
де . Говоритимемо, що оператор  визначений у просторі , якщо  для кожного .

Лема 1.  У просторі  визначений і неперервний оператор узагальненого зсуву аргументу.

Операція узагальненого зсуву аргументу  диференційовна в просторі , тобто граничне співвідношення

         

справджується за топологією простору . Як наслідок звідси дістаємо, що вказана операція є нескінченно диференційовною в просторі .

Символом  позначатимемо простір усіх лінійних неперервних функціоналів над відповідним простором основних функцій зі слабкою збіжністю, а його елементи називатимемо узагальненими функціями. Оскільки 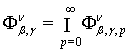, де  – поповнення  за -ою нормою, причому вкладення , , неперервні, щільні й компактні, то . Отже, кожна узагальнена функція  має скінченний порядок.

Оскільки в просторі  визначена операція узагальненого зсуву аргументу, то згортку узагальненої функції  з основною функцією задамо формулою , , при цьому  для довільної основної функції .

Нехай . Якщо , , і із співвідношення  при  за топологією простору  випливає, що  при  за топологією простору , то функціонал  називається згортувачем у просторі .

Перетворення Бесселя узагальненої функції  визначимо за допомогою співвідношення ,  (при цьому ). Звідси, з властивостей лінійності і неперервності функціоналу  та перетворення Бесселя випливає лінійність і неперервність функціоналу , заданого на просторі . Отже, .

Задача Коші. Нехай :  – неперервна, парна на  функція, однорідна порядку , нескінченно диференційовна на , похідні якої задовольняють умову:

                  (1)

З (1) випливає, що функція  є мультиплікатором у просторі . У зв’язку з цим розглянемо оператор : , який визначимо за допомогою співвідношення ,  (тут  – обернене перетворення Бесселя, яке неперервно відображає  на ). Із властивостей перетворення Бесселя (прямого й оберненого) випливає, що  – лінійний і неперервний оператор, який надалі називатимемо псевдо-Бесселевим.

Розглянемо еволюційне рівняння з оператором  вигляду

                                     (2)

де :  – неперервна функція, інтегровна на . Під розв’язком рівняння (2) розумітимемо функцію , яка задовольняє це рівняння.

Фундаментальним розв’язком рівняння (2) є функція , , де 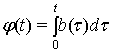. Властивості функції  наведемо в наступному твердженні.

Лема 2.  1. Функція , як функція , є елементом простору . Для функції  та її похідних справджуються оцінки

.

2. Функція , , як абстрактна функція параметра  із значеннями в просторі , диференційовна за .

3.  при  у просторі  (тут  – дельта-функція Дірака).

Наприклад, якщо , , , то , , , .

Символом  позначимо сукупність узагальнених функцій з простору , які є згортувачами в просторі .

Наслідок 1.  Нехай . Тоді

1) в просторі  справджується граничне співвідношення , ;

2) функція , , є розв’язком рівняння (2).

З наслідку 1 випливає, що задачу Коші для рівняння (2) можна ставити так: знайти розв’язок  рівняння (2), який задовольняє початкову умову

                                              (3)

в тому сенсі, що  при  у просторі . Основний результат складає наступне твердження.

Теорема 3.  Задача Коші (2), (3) є коректно розв’язною. Розв’язок подається у вигляді згортки: , , де  – фундаментальний розв’язок рівняння (2).

Нехай  – фіксоване натуральне число, , причому , , :  – неперервні, парні на  функції, диференційовні й монотонно зростаючі на , , ,  – опуклі на  функції, , , , де  – фіксований параметр; : , , – неперервні, парні на  функції, однорідні порядку  (відповідно), які задовольняють умову:

         

: , , – неперервні та інтегровні на  функції такі, що функції , , – обмежені на .

Розглянемо еволюційне рівняння

                                          (4)

де  – псевдо-Бесселевий оператор, побудований за функцією , .

Фундаментальним розв’язком (ФР) рівняння (4) є функція

         

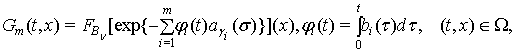
яка володіє тими ж властивостями, що і ФР рівняння (2). Зокрема, для функції  правильними є оцінки:

              (5)

де  .

Із оцінок (5) випливає, що , , при кожному . Задача Коші для рівняння (4) ставиться таким же чином, як і для рівняння (2). Підсумовуючи, сформулюємо наступне твердження.

Теорема 4.  Нехай , . Задача Коші для рівняння (4) з початковою функцією  є коректно розв’язною; її розв’язок зображається формулою , ;  при кожному .

 

Література:

1. Дрінь Я. М. Вивчення одного класу параболічних псевдодиференціальних операторів у просторах гельдерових функцій // Доп. АН УРСР. Сер. А. – 1974. – № 1. – С. 19-21.

2.   Левитан Б. И. Разложение по функциям Бесселя в ряды и интегралы Фурье // Успехи мат. наук. – 1951. – Т. 6, вып. 2. – С. 102-143.