СИНТЕЗ КОМПОЗИТОВ И МОДЕЛИРОВАНИЕ

Сорокин Д.М., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

 

Рассмотрим различные виды моделей, используемых при анализе и синтезе композиционных материалов с указанием их основных достоинств и недостатков.

Модель регрессионного ана­лиза (регрессионная модель). Используется для определения зависимости отклика от коли­чественных факторов (температура, давление, вес и т.п.)  и ошибок  наблюдения отклика:

Для -го наблюдения:

(при равноточности и некоррелированности наблюдений: , , ). Существенным ограничением метода является воздействие на отклик только количественных факторов.

Если функция отклика  есть линейная ком­бинация базисных функций от факторов, то указанная модель называется моделью регрессионного ана­лиза, линейной по параметрам или линейной моделью:

,

,  .

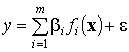Здесь  – параметры модели (коэффициенты регрессии) ;  – известные базисные функции переменных  (факторов), не зависящие от параметров модели;  – вектор-строка базисных функций (базисная вектор-функция); – вектор параметров модели.

В частном случае получается полиномиальная модель ре­грессионного анализа (полиномиальная модель), задаваемая полиномом по факторам. Ее частные случаи:

– модель регрессионного ана­лиза первого порядка (линейная модель), задавае­мая полиномом первого порядка:   (введя фиктивную переменную , модель можно пред­ста­вить в виде );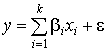

– модель регрессионного ана­лиза второго порядка (квадра­тичная модель), зада­ваемая полиномом второго порядка; (в общем случае содержит параметров):

К сожалению, регрессионные модели не обладают возможностью необходимой физической интерпретации  их коэффициентов.

Модель дисперсионного ана­лиза. Используется  для исследования зависимости отклика от качественных факторов (тип прибора, вид материала, сорт зерна и т.д.) и ошибок наблюдений отклика:

,

где — дискретные переменные, обычно целочисленные (часто  либо 0, либо 1). Наиболее простые предположения о случайных величинах те же, что и для модели регрессионного анализа. Если количественный фактор принимает в эксперименте небольшое число различных значений, то его можно рассматривать как качественный.

При детерминированных неизвестных параметрах получится модель с постоянными факторами или модель I. Модель, в которой все параметры  (может быть за исклю­чением одного) являются случайными величинами, назы­вается моделью со случайными факторами, или моделью II. В промежуточных случаях модель называется смешанной.

Метод ковариационного анализа. Используется при воздействии на отклик как количественных, так и ка­че­ствен­ных факторов;   анализ и обработка экспериментальных  производится при сочетании элементов регрессионного и дисперсион­ного анализа.

При составлении моделей в большинстве случаев используются методы планирования эксперимента. В основном используется дробный факторный план (дробная реплика полного фак­торного плана), содержащий часть комбинаций полного факторного плана. В регулярных дробных факторных планах в структуре дробных реплик сохраняются некоторые важные характеристики полного плана (например, симметрия и ортогональность; генератором плана является  алгебраическое выражение, используемое при построении дробного факторного пла­на). План эксперимента первого порядка (линейный план) – план с двумя пли более уровнями факто­ров, позволяющий найти раз­дельные оцен­ки параметров регрессионной модели перво­го порядка (называется симплекс-план, если точки размещаются в вершинах k-мерного симплекса). План эксперимента второго порядка – план с более чем двумя уровнями факторов для нахождения оценок параметров регрессионной модели второго порядка. План дисперсионного анализа – план с дискретными уровнями факторов для нахождения оценок параметров дисперсионной модели. Критерием оптимальности плана (используется более 20 раз­личных критериев оптимальности планов) чаще всего является критерий  – оптимальности (мера эффективности плана, означающая минимизацию определителя матрицы )  ,.

Приведенные методы успешно использовались при многокритериальном синтезе  композитов специального назначения повышенной плотности [1].

Литература

1.              Данилов А.М., Гарькина И.А. Теория систем: математические методы строительного материаловедения: монография. - Пенза: ПГУАС, 2008. – 379 с.