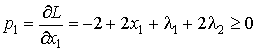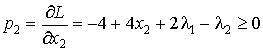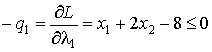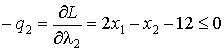НЕЛИНЕЙНЫЙ СИНТЕЗ КОМПОЗИТОВ

Капустин А.Е., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Здесь минимизируется сумма линейной и квадратичной форм при ограничениях вида линейных неравенств при неотрицательности переменных:

(1)

квадратичная форма - положительно определённая (а значит, и выпуклая; является выпуклой, если при любом 0 £ l £ 1 справедливо

).

Линейная форма – также выпуклая функция. Поэтому целевая функция будет выпуклой. Необходимые условия Куна-Таккера являются и достаточными условиями существования единственного оптимума. Для записи условий Куна-Таккера введём в рассмотрение функцию Лагранжа:

;

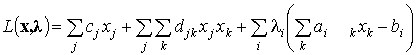производные от по x_j и l_i запишутся в виде

(2)

Требуется найти решение при условиях

(3)

(в классической задаче оптимизации определяется минимум целевой функции ; = (x₁, x₂,..., x_n) – точка в пространстве при наличии ограничений типа равенств ). При наличии ограничений минимум функции будет условным, при отсутствии - безусловным (сводится к определению и исследованию стационарных точек функции ). Классический способ решения данной задачи состоит в том, что уравнения, используются для исключения из рассмотрения m переменных. Целевая функция приводится к виду, - неисключённые переменные. Задача сводится к нахождению значений , которые обращают в минимум функцию q₁ и на которые не наложено никаких ограничений (задача на безусловный экстремум). Если ограничения имеют сложный вид, то исключение с их помощью m переменных из функции представляет значительные трудности (поэтому задачи на условный экстремум и сводятся к задаче на безусловный и используется функция Лагранжа). При большом числе переменных угадывание допустимого базисного решения становится чрезвычайно трудоёмким (используются эффективные известные систематические методы получения допустимого базисного решения).

Для иллюстрации рассмотрим задачу определения рецептурно-технологических параметров композита, при которых достигается максимальное значение прочности на сжатие (эквивалентна минимизации ). Сначала методами математического планирования эксперимента была получена аппроксимационная модель

в области факторного пространства, , .

Функция - выпуклая (сумма линейной функции и положительно-определенной квадратичной формы ). Система ограничений задачи включает только линейные неравенства; можно воспользоваться теоремой Куна-Таккера.

Функция Лагранжа:

;

необходимые и достаточные условия существования седловой точки:

, ; ,.	(4)
, ; , .	(5)

Введя дополнительные неотрицательные переменные , обращающие неравенства (4) в равенства, получим:

; , .

(6)

Из (6) следует:

, ;

, .

Отсюда базисное решение:

, ;

;

Откуда следует справедливость условий

;.

Так что является седловой точкой функции Лагранжа для исходной задачи; - оптимальный план исходной задачи; ; . Использование условий Куна-Таккера оказалось эффективным и в ряде других случаев, связанных с синтезом композиционных материалов со специальными свойствами, а также с задачами управления в эргатических системах [1].

Литература

1. Данилов А.М., Гарькина И.А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов. Строительство.– 2011. – №1. – С.80-85