Кокоева З.Т., к.п.н., доцент кафедры высшей математики ФГБОУ
ВПО «Горский государственный аграрный университет», г.Владикавказ
Кулаева Б.У., ассистент кафедры высшей математики ФГБОУ ВПО
«Горский государственный аграрный университет», г.Владикавказ
МАТЕМАТИЧЕСКИЕ РАСЧЕТЫ
В АГРОНОМИЧЕСКОЙ НАУКЕ
Применение
математических расчетов по разработке методов прогнозирования сельскохозяйственных
культур
Application
of mathematical calculation on the development of methods for forecasting of
crops
Ключевые слова:
урожай, урожайность, средняя продуктивность, прогнозирование
Key words: yield, yielding capacity, average productivity, prediction
В настоящее время развитие любой работы основано на базе
научного познания, а особенно математического, так как невозможно обойтись без
решения задач с практическим содержанием.
Эта статья написана благодаря проекту «Математика и сельское
хозяйство», который был опубликован творческим объединением «Математическая
мозаика» после проведения конкурса под названием «Применяй себя к жизни».
Основной идеей проекта является использование фактов и числовых данных,
представляющих математический и практический интерес в сельском хозяйстве для
обучения и воспитания школьников. Но желательно приблизить школьные методы
решения задач и для обучения студентов. Тема актуальна всегда и уже сейчас в
национальном проекте РФ обозначена задача возрождения сельского хозяйства,
села. В проекте сказано, что он легко модифицируется и реализуется в
разноуровневом обучении. Нужны грамотные специалисты, квалификация которых
непосредственно зависит от математической подготовки для более сложных
расчетов, а это возможно в высших учебных заведениях. Рыночная экономика меняет
требования к человеку. Студент должен обладать системой знаний, определенным
складом ума, умением принимать оптимальные решения. После окончания ВУЗов
студенты, скорее всего, возвращаются домой, и трудятся на благо своего края.
Автор проекта считает, что нужно избегать чисел, которые не
имеют под собой реальной почвы, а нужно использовать числа, взятые из
местного производства домашнего хозяйства
всего района, где живет специалист. В результате ею был составлен банк задач
(более 200) по разным темам.
Мы же взяли свою тему «Математические расчеты в
агрономической науке». Название темы кажется узкой направленности, но для
получения богатого урожая с точки зрения математики нужно привести большое
число формул, графиков, полезных агротехнических расчетов, которые представляют
математический и практический интерес в сельском хозяйстве, а также развивать у
студентов видеть жизненную задачу в
математической форме.
Применение математических методов позволяет объективно
выявлять закономерности изменчивости и наследования ценных признаков
сельскохозяйственных культур. Надо заметить, что роль математики в решении
задач селекции, сортоиспытаний и технологии выращивания зависит еще и от умения
селекционеров, агротехников и интродукторов использовать математические методы.
Наиболее чаще используются методы из математической статистики, такие как
корреляционный, дисперсионный, регрессионный анализы и так далее. Из
математического анализа употребительны дифференциальное, интегральное,
вариационное исчисления и так далее. Из теоретической кибернетики – теория
массового обслуживания, теория игр, теория распознавания образов и так далее. В
целом математический аппарат используется в задачах оптимизации технологии и
выбора оптимальных фонов выращивания и интродукции сортообразцов.
По мнению ученных-селекционеров: Андрющенко В.К., Жученко
А.А., Нестерова В.С. и других основная причина недостаточного применения
математических методов заключена в том, что для практики разработаны слишком
упрошенные модели, так как для более сложных случаев – количественных признаков
– эти модели оказываются неэффективными.
В последнее время сделаны попытки в сторону усложнения моделей: увеличили
многомерность и учет нелинейности с помощью традиционных методов. Например,
модели динамической теории биологических популяций представлены в виде систем
дифференциальных уравнений, которые учитывают большое число факторов. Но в
практической селекции с их помощью осуществлять прогноз невозможно из-за
недостатка – зависимости выходных величин от параметров, измерить которые точно
нельзя. Такими параметрами являются, например, частоты генов и аллелей, частота
кроссинговера, коэффициенты отбора на стадиях гамет и зигот и так далее. К
сожалению, математические модели разработаны лишь для определенных регионов
(агроклиматических зон) и конкретных сортов растений, а не для любых
агроклиматических условий и любого географического пункта промышленных зон возделывания,
а также не для интродукции и сортоиспытаний. Исследования по разработке нужных
моделей как математической генетики, так и теоретической кибернетики уже
начались, а пока дадим математический обзор основных методов прогнозирования
хозяйственно-ценных признаков основных сельскохозяйственных культур. Важнейшим
признаком является урожай и его качество.
Самым понятным и убедительным языком является язык цифр и фактов. Поэтому надо
выбрать такие задачи, которые связаны с выполнением практических работ на опыте
колхоза или совхоза, которые убеждают студентов в огромной роли математики в
сельском хозяйстве.
В этой статье показываем определение и подсчет урожайности
культур.
Предложенные Улановой Е.С. методы прогноза урожайности
озимой пшеницы сортов Безостая 1 и Мироновская 808, с периодом в три месяца
оправдываются до 
и осуществляются по уравнению:
, (1)
где 
- урожайность, 
;
- запасы продуктивной влаги в метровом слое почвы в декаду
возобновления вегетации, 
;
- число стеблей в 
,
сохранившихся после перезимовки.
Для составления прогноза на два месяца для озимой пшеницы
(сорта Безостая 1 и Мироновская 808) пользуются уравнением:
, (2)
где 
- средние запасы влаги в метровом слое почвы
до выхода в трубку;
- число стеблей в 
в фазу выхода в трубку;
- соответственно средняя температура и количество осадков за
период от возобновления вегетации весной до выхода в трубку.
Этот метод прогноза урожайности с уточнениями до одного
месяца был применен также Улановой Е.С. Замечено, что, если меньше период, тем
больше оправдывается: трехмесячный – до 
,
двухмесячный – до 
,
месячный – до 
.
Эта информация позволила получить более сложные и точные
уравнения связи урожайности с агрометеорологическими факторами. Ученые
Шевченко, Пасов В.М. и Коган прогнозируют ожидаемый урожай с различной заблаговременностью.
Ученые Коровин А.И. и Макиевский В.М. пользуются способом
прогнозирования в условиях перезимовки и весенних. Низкие температуры 
зимой снижают урожай (Мироновская 808) на 
,
а в сочетании с такими же весенними 
– на 
.
Ученые Дмитриенко В.П. и другие рассматривают такую модель
прогноза урожайности озимой пшеницы:
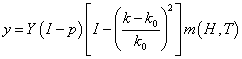, (3)
где 
- максимальная урожайность с заданной
вероятностью;
- величина средней урожайности в долях единицы;
- величины средней и оптимальной кустистости, соответственно;
- функция, значения которой определяются почвенно-климатическими
факторами за каждый период вегетации.
Для расчета максимальной урожайности колосовых культур
Дмитриенко В.П. дает уравнение в виде:
, (4)
где 
- биологическая максимальная урожайность 
на единице площади;
- оптимальное число растений на единице площади;
- оптимальная кустистость;
- оптимальное число зерен в колосе;
- оптимальная масса 
зерен, г.
Ученый Алтухов А.А. провел анализ динамики урожайности
озимой пшеницы за 
лет в Ставропольском крае и выяснил
дискретный характер ее развития с циклами 
года. Анализ изменчивости от цикла к циклу и
от периода к периоду он проводил методом построения линейной регрессии:
, (5)
где 
- урожай;
- год.
Оглоблин Е. и другие использовали уравнение:
, (6)
где 
- урожайность;
- базисная урожайность;
- стоимость техники на 
посева;
- техническая оснащенность;
- коэффициент регрессии между урожайностью и технической
оснащенностью;
- нормы внесения удобрений;
- фактическая норма удобрений на 
;
- коэффициент регрессии между урожайностью и удобрениями.
Ученые Мкртчян Р.С. и Арустамян Ш.А. разработали методику
прогноза урожайности озимой пшеницы по простейшему уравнению регрессии:
, (7)
где 
- средняя урожайность озимой пшеницы старых
сортов по 
административным районам республики (страны)
Армении;
- средние запасы влаги в полуметровом слое почвы к моменту
возобновления вегетации.
Методы прогнозирования урожая зерна кукурузы разработаны
Чирковым Ю.И. и основаны на учете площади листовой поверхности и запасов
продуктивной влаги (в слое почвы 
)
и обеспеченности теплом. Уравнение для расчета урожая:
, (8)
где 
- запасы продуктивной влаги в слое почвы 
;
- поправочный коэффициент на температуру. При этом коэффициенты 
определяются в соответствии с размерами
площади листовой поверхности.
Чирков Ю.И. отмечает, что ведущими факторами являются свет,
тепло и влага. Анализируя такие показатели как вес растительной массы кукурузы 
и площадь листовой поверхности 
,
он определяет интенсивность накопления растительной массы с помощью отношения 
.
Этот показатель позволил независимо от фазы развития, мощности растений и
густоты посева сопоставлять материалы по приросту растительной массы. По этим
данным были составлены уравнения линейной регрессии, позволяющие производить
прогноз биологического урожая растительной массы на посевах кукурузы.
В настоящее время имеется очень много литературы с описанием
все новых методов и результатов изучения потенциальной продуктовности
возделываемых видов и сортов культурных растений, обеспечиваемой генотипом и
ресурсами климата, плодородием почвы, состоянием экономических,
материально-технических, социальных и моральных факторов, прогнозом возможного
повышения генетического потенциала продуктивности в связи с применением новых
методов селекции и изменением климата. Одна из книг из этой литературы
принадлежит крупнейшему ученому Образцову А.С. «Потенциальная продуктивность
культурных растений», – Москва: ФГНУ «Росинформагротех», 2010г
В этой книге понятие «продуктивность» рассматривается как
понятие «урожайность», что означает способность растительных сообществ
обеспечивать получение того или иного количества используемой растительной
продукции за период вегетации. «Урожайность» и «Урожай» не тождественны. «Урожай» - это конкретное количество уже
полученной используемой продукции в данном году или в любом каком-либо из
предыдущих лет. Урожайность определяется по величине урожаев в течение ряда лет
в конкретных условиях.
Рассмотренные нами формулы составляют лишь мизерную часть
огромного количества уравнений, известных и в нашей стране и за рубежом, но они
убеждают в необходимой роли математики в сельском хозяйстве. Расширены познания
и кругозор студентов, так как при хорошей математической подготовке можно
выполнять сложные расчеты.
Решение практических задач в сельском хозяйстве с помощью
математических формул поможет будущим молодым специалистам сельского хозяйства
сознательно применять полученные знания при планировании, организации
деятельности, экономии, подборе материала и так далее
Литература
1. Аграфонова С.А. Проект «Математика и
сельское хозяйство». – Староюрьево, тамбовская область: Творческое объединение
«Математическая мозаика», 2011г
2. Жученко А.А., Нестеров ВС., Добрянский
В.А. Математическое моделирование при оптимизации селекционно-генетических
исследований. – Кишинев: «Штиница», 2000г
3. Образцов А.С. Потенциальная
продуктивность культурных растений. – Москва: ФГНУ «Росинформагротех», 2010г