Динамика научных исследований

05.07.2014

07 - 15 июля 2014 г.

Польша

Динамика научных исследований:

«Внедрение информационных технологий в развитие исследовательской компетенции».

Автор: Рамазанова Гелин Магамедшерифовна,учитель физики МКОУ «СОШ №14» с.Надежда Шпаковского района Ставропольского района

helin.ramazanova@yandex.ru – электронный адрес

Умственная деятельность везде является той же

самой, на переднем ли фронте науки или в

третьем классе школы. Различие здесь в степени,

а не в роде. Школьник, изучающий физику,

является физиком, и для него легче изучать

науку, действуя подобно ученому-физику, чем

делать что-либо еще.

Дж.Брунер

Компонентами любой исследовательской деятельности, независимо от области приложения, являются: владение умениями выдвижения гипотез и их проверки для исследования простейших явлений, элементарными умениями прогноза, самостоятельного планирования действий для решения задач творческого и поискового характера. В данной работе предлагается вариант организации учебного исследования с применением новых информационных технологий на основе задачного подхода к обучению физике в профильной школе. Использование информационных технологий в этой связи является не данью моде, а отражением изменений, которые объективно произошли в физике в последние десятилетия и связаны с расширением исследовательского инструментария: для исследований кроме теоретических и экспериментальных стали широко применяться вычислительные методы и методы математического моделирования.

В течение длительного времени обучение физике основывалось на ис-пользовании учебных задач, решение которых может быть получено анали-тическими методами. Повсеместное внедрение компьютеров в процесс обучения привело к возможности постановки учебных задач, решение ко-торых может быть получено в результате численных расчетов.

При этом грамотная методическая работа в этом направлении должна быть связана с обучением учащихся разработке физических и математиче-ских моделей явлений природы, проведению комплексных теоретических, экспериментальных и вычислительных исследований этих моделей и пра-вильной интерпретации полученных результатов, что естественным обра-зом опирается на решение физических задач. В такой трактовке обучение элементам компьютерного моделирования является наиболее адекватным методом включения компьютера в обучение, обеспечивающим не только высокий уровень наглядности, но и активные виды учебной деятельности.

Задачный подход к обучению, или «обучение через задачи», представ-ляет собой разновидность проблемного обучения, которое основано на применении системы задач, объединенных между собой общей идеей ис-следования, ориентированной на получение новых (субъективно) теорети-ческих знаний. При этом система задач должна удовлетворять следующим требованиям [1]:

Ÿ допускать возможность различной последовательности рассмотрения предлагаемых задач, позволяя тем самым достичь необходимого уровня понимания изучаемого вопроса не единственным образом;

Ÿ предоставлять возможность для продолжения и развития анализа си-туаций, выходящих за рамки исходной формулировки, путем изменения проблемы и спектра вопросов, переосмысления имеющихся знаний;

Ÿ допускать применение физических законов разных методологиче-ских уровней;

Ÿ содержать задачи, относящиеся к различным разделам физики, но предоставляющие возможность обратить особое внимание на какой-то оп-ределенный компонент действий в цикле математического моделирования;

Ÿ в условии задачи особое внимание должно обращаться не на исчерпы-вающую постановку вопроса, а на поиск круга вопросов, на которые можно найти ответы в рамках рассматриваемой модели изучаемого явления;

Ÿ необходимым действием должно быть установление области спра-ведливости ответа (границ применимости модели) еще до получения его в явном виде.

Рассмотрим пример реализации такого подхода.

В углах правильного тетраэдра находятся четыре мухи. В нулевой момент времени мухи начинают полет, причем модуль скорости каждой из мух постоянен. При полете первая муха всегда летит в направлении второй, вторая – в направлении третей, третья – в направлении первой, четвертая – также в направлении первой. Рассчитайте траекторию полета мух. Через какое время мухи встретятся?

Результаты численного расчета представлены на рис.1.

Особое значение приобретают компьютерные вычисления в тех случаях, когда воспользоваться физическими законами, изучаемыми в школе, невозможно из-за нарушения границ их применимости. Так, например, закон Кулона

F = q1.q2/r2

применим только для точечных электрических зарядов, а следовательно, сила взаимодействия протяженных заряженных тел даже правильной гео-метрической формы требует более серьезных математических расчетов, которые вполне возможно выполнить компьютерными методами в виде ученической исследовательской работы.

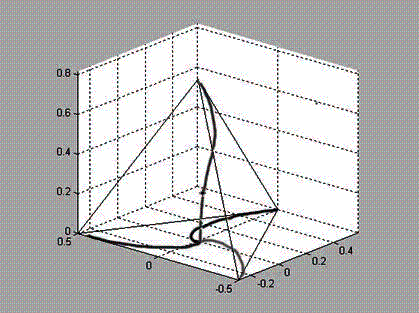
Рис1. Траектории движения мух. Звездочкой помечено положение 4-й мухи в момент времени встречи первых трех мух, первая муха движется из правого угла тетраэдра

II. Взаимодействие заряженных металлических шаров.

Поставить проблему исследования можно в ходе решения известной задачи [4].

Почему два разноименно заряженных металлических шара взаимодействуют с большей силой, нежели заряженные одноименно? Возможно ли, чтобы два одноименно заряженных проводника притягивались?

Качественное объяснение данному явлению можно дать на основе явления электростатической индукции. Действие электрических полей, создаваемых заряженными шарами, приводит к тому, что заряды на шарах, располо-женных достаточно близко друг от друга (их нельзя считать материальными точками), перераспределяются. При этом одноименные заряды окажутся на большем расстоянии, чем разноименные, поэтому взаимодействие разноименно заряженных шаров при прочих равных условиях оказывается более сильным. Одноименно заряженные металлические шары могут даже притягивать-ся, если заряд одного много больше заряда другого (рис. 3, 4).

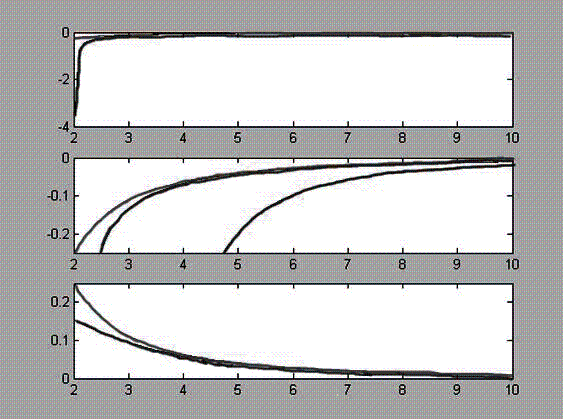
Рис. 2. Результаты численных расчетов.

Логическим продолжением решения этой задачи может быть количе-ственный расчет силы взаимодействия заряженных металлических сфер.

Вычислите силу взаимодействия двух металлических сфер одинакового радиуса R, заряженных одинаковыми по модулю зарядами. Рассмотрите случаи, когда заряды имеют одинаковые и разные знаки. Постройте графики зависимости силы взаимодействия от расстояния между цен-трами сфер r.

Так как при сближении сфер распределение зарядов на них становится несимметричным, то для непосредственного применения закона Кулона необходимо знать поверхностную плотность заряда в каждой точке каждой из сфер. Избежать необходимости вычисления силы взаимодействия каждой точки одного тела с каждой точкой другого и последующего громоздкого суммирования можно с помощью метода зеркального изображения. Так, например, решается задача о взаимодействии точечного заряда с бесконеч-ной металлической плоскостью, в соответствии с которым металлическая плоскость заменяется зарядом с противоположным знаком, расположенным зеркально симметрично по отношению к исходному заряду. Решить поставленную задачу можно, применяя метод зеркального изображения и метод последовательного приближения, на основе которых организуются циклические вычисления с помощью какого-либо пакета математических программ или языков программирования, изучаемых в школе. . Здесь на рис. 2 приведены результаты численных расчетов, подтверждающие качественные выводы, полученные выше. На верхнем графике приведены сила взаимодействия разноименно заряженных сфер (нижняя кривая) и сила взаимодействия двух точечных зарядов. Отрицательные значения силы соответствуют притяжению. Заметим, что если исходить из физического смысла, то сила притяжения между сферами при r - 2 по модулю неограниченно возрастает, поскольку при этом положительный и отрицательный заряды сближаются на бесконечно малое расстояние. Поэтому вычисление ограничено величиной r min = 2,01.

На среднем графике те же величины приведены в ограниченном масштабе по вертикальной оси. Минимальное значение силы ограничено соо-ветствующим значением для двух точечных зарядов. Самая нижняя кривая соответствует значению силы Fn

На нижнем графике изображены значения силы отталкивания двух од-ноименно заряженных сфер (нижняя кривая) и двух точечных зарядов.

Большие информационные потоки, с которыми сталкивается сегодня каждый человек, требуют от системы общего образования решения задач обучения молодых граждан способам работы с информацией. Это, кроме того, открывает широкие возможности для построения учебного процесса, учитывающего индивидуальные возможности и склонности обучающихся, их включения в самостоятельную исследовательскую деятельность, что, в свою очередь, способствует созданию условий для максимальной реализации каждого.

Новые цели и образовательные задачи приводят к необходимости переосмысления места традиционных образовательных технологий в образовательном пространстве школы и к разработке современной дидактической системы, основанной на использовании средств ИКТ.

Литература

1.Кондратьев А.С., Ляпцев А.В. Физика. Задачи на компьютере. – М.: Физ-матлит, 2008.

3. Гельфгафт И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с решениями: Учеб. пособие. – Харьков – Москва: Центр «Инновации в нау-ке, технике, образовании», 1996.

4. Гольдфарб Н.И. Сборник вопросов и задач по физике. – М., 1978.