Математика/1.Дифференциальные и интегральные уравнения

Д.ф.-м.н. Городецький В. В.

Чернівецький національний університет імені Юрія Федьковича,Україна

Багатоточкова за часом задача для еволюційних псевдодиференціальних рівнянь із аналітичними символами

Нелокальні крайові задачі для диференціально-операторних рівнянь та рівнянь з частинними похідними виникають при побудові загальної теорії крайових задач, описуванні всіх коректних задач для конкретного оператора, математичному моделюванні різноманітних природничих процесів. Дослідженням нелокальних крайових задач у різних аспектах займалося багато математиків, використовуючи при цьому різні методи та підходи (О. О. Дезін, В. К. Романко, С. Г. Крейн, Б. Й. Пташник, В. І. Чесалін [1-5] та ін.). Одержані важливі результати щодо постановки, коректної розв’язності та побудови розв’язків, досліджені питання залежності характеру розв’язності задач від поведінки символів операцій, сформульовані умови регулярності та нерегулярності крайових умов для важливих випадків диференціально-операторних рівнянь.

У цій роботі досліджена нелокальна багатоточкова за часом задача для еволюційних рівнянь з псевдо диференціальними операторами, побудованими за символами, які допускають аналітичне продовження у певну область комплексної площини (клас таких операторів містить і оператори Бесселя дробового диференціювання). Встановлена структура та властивості фундаментального розв’язку, коректна розв’язність задачі у випадку, коли гранична функція є узагальненою функцією типу ультрарозподілів, знайдено зображення розв’язку у вигляді згортки фундаментального розв’язку з граничною функцією, встановлена властивість локалізації розв’язку багато точкової задачі.

Нехай , – фіксовані параметри. Символом позначимо сукупність функцій , які задовольняють умови: 1) функція нескінченно диференційована на , при цьому :

: ;

2) функція допускає аналітичне продовження в область

комплексної площини; функція , , задовольняє нерівність

,

з деякими сталими , залежними лише від функції . З теореми типу Фрагмена-Ліндельофа [6, c. 264] випливає, що похідні функції на дійсній осі задовольняють нерівності

,

з деякими сталими . Звідси дістаємо, що є елементом простору , який відноситься до просторів типу , введених в [6]. Простори типу складаються з нескінченно диференційованих функцій, заданих на , на які накладаються певні умови спадання на нескінченності та зростання похідних. Ці умови задаються за допомогою нерівностей , , де – деяка подвійна послідовність додатних чисел. Якщо на елементи послідовності не накладаються жодні обмеження (тобто можуть змінюватися довільно разом з функцією ), то маємо, очевидно, простір Л. Шварца швидко спадних на нескінченності функцій. Якщо ж задовольняють певні умови, то відповідні конкретні простори містяться в і називаються просторами типу . Зокрема, для довільних фіксованих

:.

Простір можна охарактеризувати ще так [6]. складається з тих і тільки тих нескінченно диференційованих на функцій, які задовольняють нерівності , , з деякими додатними сталими , залежними від функції .

Якщо і , то складається з тих і лише тих функцій , які допускають аналітичне продовження в комплексну площину і задовольняють нерівність

, .

Топологічна структура в просторах визначається так. Символом позначимо сукупність функцій , які задовольняють умову:

, .

Ця множина перетворюється в повний зліченно-нормований простір, якщо норми в ній ввести за допомогою співвідношень

.

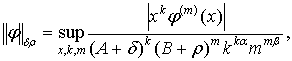
Якщо , то неперервно вкладається в і =. Отже, в можна ввести топологію індуктивної границі просторів [6].

У просторах визначена і є неперервною операція зсуву аргументу . Ця операція є також диференційованою (навіть нескінченно диференційованою [6]) у тому розумінні, що граничне співвідношення , справджується для кожної функції в сенсі збіжності за топологією простору . У визначена і неперервна операція диференціювання. Простори типу є досконалими [6] (тобто просторами, всі обмежені множини яких компактні), вони тісно пов’язуються між собою перетворенням Фур’є, а саме, правильними є формули:

=, .

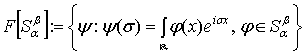Символом позначимо простір усіх лінійних неперервних функціоналів на зі слабкою збіжністю. Оскільки при в () є й фінітні функції [6], то має сенс наступне означення: узагальнена функція (, ) дорівнює нулеві на інтервалі , якщо для довільної функції , носій якої міститься в (тут позначає дію функціоналу на основну функцію ). Оскільки в основному просторі визначена операція зсуву аргументу, то згортку узагальненої функції з основною функцією задамо формулою

.

Із властивості нескінченної диференційовності операції зсуву аргументу в просторі випливає, що згортка є звичайною нескінченно диференційовною на функцією.

Оскільки =, то перетворення Фур’є узагальненої функції означимо так: .

З умови 1) випливає, що функція – мультиплікатор у . Оскільки (), то функція є мультиплікатором і у просторі . Зокрема, , , належить до класу і є мультиплікатором у просторі (а також у , ), .

Візьмемо функцію з класу . Із властивостей цієї функції випливає, що в просторі визначений, є лінійним і неперервним оператор , побудований за функцією як за символом за правилом: , .

Якщо , то, як відомо [7, c.395], оператор представляє собою конструктивну реалізацію оператора , , , який (див. [7]) називається оператором Бесселя дробового диференціювання.

Для еволюційного рівняння

, (1)

де – оператор, побудований вище, розглянемо нелокальну багатоточкову (-точкову) за часом задачу: знайти розв’язок рівняння (1), який задовольняє умову:

(2)

де , , , – фіксовані числа, , . Скориставшись методом перетворення Фур’є знайдемо, що розв’язок задачі (1), (2) має вигляд:

, ,

, .

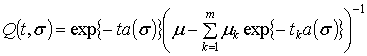Основні властивості функції наведемо в наступних твердженнях.

Лема 1. Для функції та її похідних справджуються нерівності

, (3)

, ,, сталі не залежать від .

Лема 2. Функція ,, як абстрактна функція параметра із значеннями в просторі , диференційовна по .

Лема 3. У просторі справджується граничне співвідношення ( – дельта-функція Дірака).

Із оцінок (3) випливає, що є елементом простору при кожному . Отже, має зміст згортка , де – узагальнена функція з простору . Символом позначимо клас узагальнених функцій з , які є згортувачами в просторі . З леми 3 випливає наступне твердження.

Наслідок 1. Нехай , , . Тоді в просторі правильним є граничне співвідношення

.

Зауважимо також, що є розв’язком рівняння (1). Надалі функцію називатимемо фундаментальним розв’язком -точкової задачі для рівняння (1) (позначення: ФРБЗ).

З наслідку 1 випливає, що для рівняння (1) -точкову за часом задачу можна ставити так: знайти розв’язок рівняння (1), який задовольняє умову

, , (4)

де границі розглядаються в просторі . Правильним є наступне твердження.

Теорема 1. Задача (1), (4) коректно розв’язна. Розв’язок зображається у вигляді згортки: , , де – ФРБЗ для рівняння (1), при кожному .

Оскільки узагальнена функція – згортувач у просторі , а функція є неперевною абстрактною функцією параметра із значеннями в просторі , то граничні співвідношення , , , справджується в просторі . Звідси, зокрема, дістаємо, що при , , рівномірно на довільному відрізку . Вказану збіжність в (4) погіршує перший доданок, оскільки для функції точка є особливою. Однак, якщо граничну функцію брати з класу , де , то можна отримати локальне покращення збіжності згортки при . Це пояснюється тим, що клас при містить фінітні функції і в цьому випадку коректним є поняття збіжності узагальненої функції з гладкою функцією на деякій відкритій множині . Символом позначимо клас функцій, які є мультиплікаторами в просторі , .

Теорема 2 (властивість локалізації). Нехай , де , – розв’язок задачі (1), (4)з граничною функцією . Якщо узагальнена функція збігається на інтервалі з функцією , то на довільному проміжку граничне співвідношення

справджується рівномірно відносно .

Література:

1. Дезин А. А. Операторы с первой производной по «времени» и нелокальные граничные условия // Изв. АН СССР. Сер. Мат. – 1967. – Т.31, №1. – С. 61-86.

2. Романко В. К. Граничные задачи для некоторых дифференциально-операторных уравнений // Докл. АН СССР. – 1976. – Т.227, №4. – С. 812-816.

3. Крейн С. Г., Лаптев Г. И. Граничные задачи для дифференциальных уравнений второго порядка в банаховом пространстве // Дифференц. уравнения. – 1966. – Т.2, №3. – С. 382-390.

4. Пташник Б. Й., Ільків В. С., Кміть І. Я., Поліщук В. П. Нелокальні крайові задачі для рівнянь з частинними похідними. – Київ: Наук. думка, 2002. – 416 с.

5. Чесалін В. И. Задача с нелокальными граничными условиями для некоторых абстрактных гиперболических уравнений // Дифференц. уравнения. – 1979. – Т.15, №11. – С. 2104-2106.

6. Гельфанд И. М., Шилов Г. Е. Пространства основных и обобщенных функций. – М.: Физматгиз, 1958. – 307 с.

7. Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. – 688с.