Янковська О

Янковська О.М.

Національний технічний університет України «Київський політехнічний інститут»

ОПТИМАЛЬНИЙ РОЗПОДІЛ РЕАКТИВНИХ ПОТУЖНОСТЕЙ

Питання розподілу реактивної потужності привертають все більшу увагу дослідників та інженерів-практиків. Дослідження проблеми реактивної потужності фактично виходить за межі задачі розподілу. Особливо необхідно відзначити роботи з уточнення поняття реактивної потужності та її математичної та фізичної інтерпретації. Проблема в цілому є предметом особливого дослідження. Наведені нижче матеріали слід розглядати як представлення деяких окремих випадків вирішення завдань про розподіл реактивних потужностей.

Спосіб Брехта

Брехт вважає, що розподіл реактивної потужності слід обумовити мінімумом втрат на нагрівання і, що цей мінімум має місце, коли лінія передачі, що зв'язує паралельно працюючі установки, передає реактивний струм певної величини, і зсуву фаз в лінії передачі може бути відмінний від зсуву фаз в окремих установках.

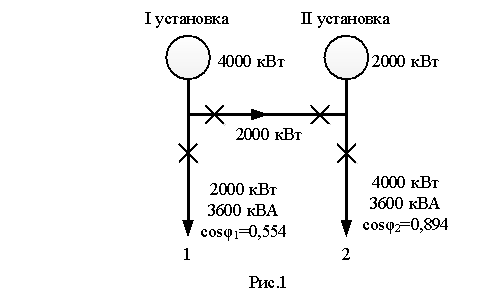
Розглянемо спільну роботу двох установок, пов'язаних лінією передачі (рис. 1 і 2).

Позначимо:

активна потужність установок,

активна потужність мережі,

реактивна потужність мережі,

позірна потужність мережі,

потужність, що передається від першої установки до другої установки за допомогою лінії передач. Вважаємо, що і , задані і розподілені довільно.

В обох установках необхідно виробити певну кількість реактивної енергії для покриття реактивної потужності мережі

Завдання може бути сформульована таким чином: як розподілити між двома установками і який зсув фаз ψ₁і ψ₂ необхідно встановити для того, щоб втрати, які залежать від коефіцієнта потужності в установках та мережі, складали мінімум.

У генераторній частині від коефіцієнта потужності і збудження залежать втрати на збудження, втрати в залізі, втрати на нагрів. У трансформаторах, в розподільчому пристрої та лінії враховуємо, головним чином, втрати на нагрів.

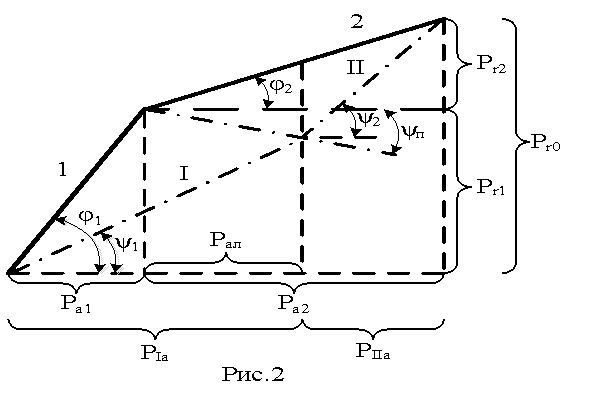
Достатньо знайти такий струморозподіл, при якому втрати на нагрів в системі: перша установка – лінія – друга установка будуть мінімальні. Якщо позначити омічний опір відповідно через R₁, R_л і R₂ і для струму прийняти позначення діаграми рис.2, раніше нами прийняті для позначення потужності, тому втрати на нагрів будуть дорівнювати

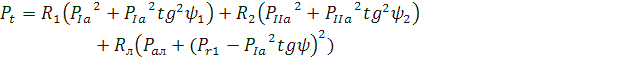
крім, того

Всі члени, які не залежать від tg φ, збираємо разом.

Тоді

і умови мінімуму:

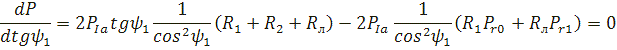
Вводимо коефіцієнти:

Отримаємо:

Останнє рівняння показує, що в лінії поряд з активною потужністю необхідно передати реактивну потужність , для того щоб сума втрат була мінімальна.

Із вищенаведеного виразу видно, що зсув фаз, який забезпечує мінімум втрат, буде тим менше, чим більша потужність, що передається лінією, і чим більший її опір і опір інших частин установок.

Наступний приклад дає наочну ілюстрацію. Вводимо замість абсолютних величин відносні величини:

Із цього виразу отримуємо найбільш економічний розподіл.

На графіку рис.3 наведені залежність втрат окремих установок і в лінії передач, сумарні втрати на нагрівання від реактивного струму в лінії передачі. Виконавши аналіз, можна прийти до практичного висновку, що прагнення досягти відповідності зсуву фаз в лінії передачі із зсувом фаз в установках є помилковим, негативний кут ψ, тобто випереджувальний струм, на лінії передачі економічно необхідний.