Технические науки/6. Электротехника и радиоэлектроника
Д.т.н. Митрофанов Д.Г., Майоров Д.А., Бортовик В.В., Кичулкин Д.А.
Общество с
ограниченной ответственностью "Смоленский
научно-инновационный
центр радиоэлектронных систем "ЗАВАНТ", Россия
АНАЛИТИЧЕСКАЯ МОДЕЛЬ ИМПУЛЬСНОЙ
ХАРАКТЕРИСТИКИ ЛЕТАТЕЛЬНОГО АППАРАТА
На современном этапе развития радиолокационных методов
извлечения информации об объектах разработчиков радиолокационных систем уже не
устраивают традиционные сведения о координатах и параметрах движения наблюдаемых
целей. Переход к цифровым методам обработки отраженных сигналов расширил
диапазоны измеряемых параметров объектов, что привело к появлению в
разрабатываемых образцах локаторов особых режимов, позволяющих выявлять число
объектов в неразрешаемом объеме, конфигурационные особенности объектов и т.д.
Например, в работе [1] высокого продольного разрешения добиваются применением
сверхкоротких импульсов длительностью 7 нс, а в работе [2] показаны продольные
портреты с высоким разрешением за счет доведения девиации линейно-частотно-модулированных
импульсных сигналов до сотен МГц. В типовых РЛС такие режимы и сигналы не
используются в виду необходимлсти усложнения приемопередающих трактов, однако
задача расширения информативности с повестки дня не снимается.
Одним из подходов к реализации в типовых импульсных
РЛС методов повышения разрешающей способности является применение режима
перестройки несущей частоты заполнения стандартных импульсных сигналов, причем
каждый отдельный радиоимпульс остается при этом узкополосным, т.е. квазимонохроматическим.
Согласно свойствам тела неопределенности [3] повышения разрешающей способности
по дальности (вдоль линии визирования) можно добиться расширением ширины
спектра сигнала. Указанное расширение может быть следствием уменьшения
длительности зондирующего сигнала [1], увеличения девиации внутри импульса [2],
а также применения внутрипачечной частотной модуляции [4]. Облучение каждого
отдельного рассеивающего центра (РЦ) сверхкоротким наносекундным импульсом
приводит к формированию импульсной характеристики отражения. Совокупность
импульсных характеристик от отдельных РЦ поверхности объекта будем называть
импульсной характеристикой (ИХ) объекта [5], в том числе и летательного
аппарата. Если вместо сверхкороткого импульса применить пачку сигналов с
перестройкой частоты (СПЧ), имеющую такую же общую ширину спектра, как и
сверкороткий импульс, то должен достигаться аналогичный эффект повышения
разрешающей способности и формирования ИХ объекта. В данном случае ИХ объекта
может быть получена лишь при совместной обработке всех отраженных сигналов пачки
СПЧ, так как только в этом случае можно говорить о применении сигнала с большой
шириной спектра.
Итак, под импульсной характеристикой будем понимать
совокупность импульсных откликов от рассеивающих центров (РЦ) поверхности
объекта на облучение их сигналом с широкой полосой частот. В интересах
увеличения дальности действия и упрощения конструкции радиолокатора облучение целесообразно
производить не коротким импульсом, а последовательностью обычных микросекундных
импульсов с последовательной монотонной или случайной перестройкой несущей
частоты от одного импульса к другому. Общий диапазон изменения несущей частоты
в пачке СПЧ должен составлять не менее сотен МГц (например, 150 МГц), что при
совместной обработке отраженных сигналов эквивалентно зондированию
сверхкоротким импульсом. Использование СПЧ, а не импульса с малой
длительностью, рекомендовано кроме всего прочего в связи с возможностью
повышения отношения сигнал-шум при совместной когерентной обработке СПЧ.
Для формирования информативной ИХ летательного
аппарата (ЛА) требуется наоборот использовать длительность пачки СПЧ, не
превышающую величины интервала угловой корреляции (ИУК) Тук, который
для отраженных летательным аппаратом сигналов определяется по формуле
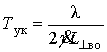 , (1)
, (1)
где
l - средняя длина волны, ![]() - угловая скорость поворота ЛА относительно линии визирования;
L^во –
поперечный размер ЛА в момент измерения.
- угловая скорость поворота ЛА относительно линии визирования;
L^во –
поперечный размер ЛА в момент измерения.
Если не выходить за пределы ИУК, то все импульсы пачки
СПЧ, после устранения фазовых сдвигов, связанных с поступательным движением ЛА,
можно условно считать отраженными от неподвижного объекта. Иначе говоря, при
таком зондировании даже поворачивающийся объект (ЛА), можно с высокой степенью
приближения считать неподвижным. Именно при таком условии можно сформировать
эталонную ИХ ЛА, т.е. ИХ без искажений и расширений (размываний) временных
откликов.
Наименьший ИУК в диапазоне сантиметровых волн соответствует
наблюдению самого крупногабаритного ЛА (L^во=70 м),
имеющего максимальную угловую скорость рысканий планера (порядка 2о/с).
Для гарантированного обеспечения корреляции между принимаемыми локатором СПЧ следует
использовать величину Тук,
не превышающую 5 мс.
Вектор ИХ целесообразно получать методом обратного
быстрого преобразования Фурье (БПФ) из массива отраженных СПЧ, в котором
комплексные или квадратурные данные об амплитудно-фазовых параметрах отражения
располагаются в порядке, соответствующем монотонному увеличению частоты излучения.
Такой вектор (совокупность данных) отражений будем называть комплексной
частотной характеристикой (КЧХ) объекта.
В формируемой в процессе приема и обработки отраженных
сигналов КЧХ фазовые значения отражений должны быть обусловлены только взаимным
продольным распределением РЦ на освещенной поверхности планера ЛА, а фазовые
сдвиги, связанные с поступательным движением корпуса ЛА, должны быть устранены.
Для устранения этих фазовых сдвигов дальностной природы может использоваться
рекуррентный алгоритм вычитания из фазы принятого сигнала фазового компонента,
обусловленного исключительно изменением расстояния до объекта. Использование
пошаговых рекуррентных расчетов нужно лишь в случае использования вобуляции
частоты повторения Fи импульсов. Если же период повторения
импульсов Ти постоянен, то
компенсацию можно проводить по универсальной формуле, приведенной в [6,7].
Однако оба эти подхода предполагают знание радиальной скорости Vr
движения ЛА, вычисляемой на предварительном этапе стандартным методом в режиме
одночастотного зондирования [6]. Если в интересах помехоустойчивости применять
только СПЧ, то для устранения фазовых набегов радиального (поступательного)
характера целесообразно рекомендовать способ, описанный в [7,8]. Этот способ построения
информативной ИХ и оценки радиальной скорости ЛА сам по сути своей основан на
компенсации рассматриваемых фазовых сдвигов, обусловленных его радиальным движением.
Соблюдение временных ограничений и компенсация фазовых
сдвигов, обусловленных радиальными смещениями, гипотетически должно приводить к
улучшению информационных свойств формируемой ИХ, так как обеспечивает
воображаемое замирание ЛА в пространстве, что стабилизирует радиолокационные
измерения.
Для демонстрации потенциальных возможностей ИХ
воспроизводить продольную структуру объекта необходимо получить ее
аналитическую (математическую) модель, которая позволяла бы исследовать
свойства ИХ. Попытки получить выражение для описания ИХ ранее уже предпринимались
[9,10]. Однако в предполагаемых аппроксимирующих преобразованиях использована
идеализация, связанная с заменой импульсного сигнала непрерывной функцией,
позволяющей использовать в качестве аппарата преобразования интегрирование, что
не соответствует реальной обработке.
Целью настоящей статьи является получение более
адекватной аналитической модели ИХ объекта, соответствующей условиям приема и
обработки отраженных импульсных СПЧ.
Математической
моделью пачки зондирующих СПЧ является пачка из N эквидистантных
импульсов, модулированная по амплитуде по закону ![]() с линейным ступенчатым
изменением частоты. Модель имеет аналитическую запись вида
с линейным ступенчатым
изменением частоты. Модель имеет аналитическую запись вида
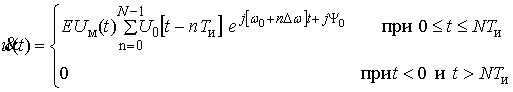 , (2)
, (2)
где Е
- максимальная
амплитуда импульса; ![]() -
закон модуляции отдельного радиоимпульса во времени t; n – номер импульса в пачке; Dw =2pDf – шаг перестройки круговой частоты w=2pf; N – число радиоимпульсов в пачке, равное количеству
фиксированных частот перестройки; w0 - основная циклическая несущая частота; Y0 - начальная фаза отдельного радиоимпульса.
-
закон модуляции отдельного радиоимпульса во времени t; n – номер импульса в пачке; Dw =2pDf – шаг перестройки круговой частоты w=2pf; N – число радиоимпульсов в пачке, равное количеству
фиксированных частот перестройки; w0 - основная циклическая несущая частота; Y0 - начальная фаза отдельного радиоимпульса.
На рис. 1 показана одна из
квадратурных составляющих последовательности импульсов с линейной ступенчатой
перестройкой частоты в предположении прямоугольной модуляции всей
последовательности и каждого импульса в отдельности.
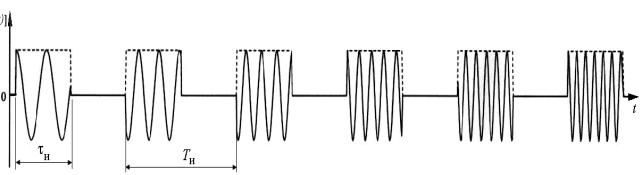 Рис. 1
Рис. 1
Без учета интерференционной модуляции волн математическая модель пачки СПЧ, отраженной от отдельного m-го РЦ, в общем виде может быть выражена
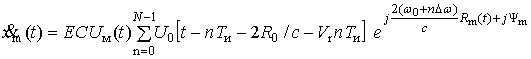 (3)
(3)
![]() ,
,
где C - коэффициент, зависящий
от усилительных свойств приемной системы; ![]() - начальная дальность до объекта;
с – скорость распространения
радиоволн;
- начальная дальность до объекта;
с – скорость распространения
радиоволн; ![]() - функция, описывающая изменение удаления m-го
РЦ с течением времени;
- функция, описывающая изменение удаления m-го
РЦ с течением времени; ![]() – проекция радиус-вектора между центром сопровождения объекта
(ЦСО) и m-м РЦ на радиальное
направление в момент начала излучения пачки СПЧ;
– проекция радиус-вектора между центром сопровождения объекта
(ЦСО) и m-м РЦ на радиальное
направление в момент начала излучения пачки СПЧ; ![]() – проекция радиус-вектора между ЦСО и m-м РЦ на
перпендикулярное относительно линии визирования направление в момент начала
излучения;
– проекция радиус-вектора между ЦСО и m-м РЦ на
перпендикулярное относительно линии визирования направление в момент начала
излучения; ![]() – средняя на
интервале излучения СПЧ угловая скорость поворота ЛА; Ym
– фазовый сдвиг, возникающий при отражении от m-го РЦ.
– средняя на
интервале излучения СПЧ угловая скорость поворота ЛА; Ym
– фазовый сдвиг, возникающий при отражении от m-го РЦ.
Полный вектор отражений последовательности СПЧ имеет вид
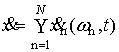 , (4)
, (4)
где ![]() -
комплексный отраженный ЛА сигнал на n-й частоте в момент времени t. Комплексность
предполагает наличие квадратурных составляющих (Imn и Ren) n-го отраженного сигнала в пике отклика
согласованного фильтра на указанный отраженный сигнал, что позволяет привести
(преобразовать) такой квадратурный отраженный сигнал n-й частоты к комплексному виду Аnexp(jjn) по формуле Эйлера, Аn - амплитуда n-го отраженного импульса, jn - его
фаза.
-
комплексный отраженный ЛА сигнал на n-й частоте в момент времени t. Комплексность
предполагает наличие квадратурных составляющих (Imn и Ren) n-го отраженного сигнала в пике отклика
согласованного фильтра на указанный отраженный сигнал, что позволяет привести
(преобразовать) такой квадратурный отраженный сигнал n-й частоты к комплексному виду Аnexp(jjn) по формуле Эйлера, Аn - амплитуда n-го отраженного импульса, jn - его
фаза.
Принятый
локатором на n-й частоте ![]() сигнал, отраженный в
зоне Фраунгофера от совокупности из М
РЦ освещенной поверхности объекта, каждый
m-й из которых имеет
эффективную отражающую площадь sm,
определяется выражением
сигнал, отраженный в
зоне Фраунгофера от совокупности из М
РЦ освещенной поверхности объекта, каждый
m-й из которых имеет
эффективную отражающую площадь sm,
определяется выражением
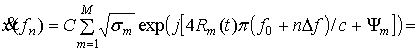
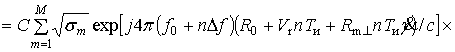 (5)
(5)
![]() .
.
В виду малости
угловой скорости ![]() поворота ЛА и длительности
пачки СПЧ nTи величиной
поворота ЛА и длительности
пачки СПЧ nTи величиной ![]() можно пренебречь. Действительно
даже при повороте ЛА с максимальной скоростью
можно пренебречь. Действительно
даже при повороте ЛА с максимальной скоростью ![]() 2о/с, при периоде Ти=10 мкс, числе частот N=128 и поперечном
удалении РЦ
2о/с, при периоде Ти=10 мкс, числе частот N=128 и поперечном
удалении РЦ ![]() 25 м его продольное смещение составит около 1 мм. Другие
составляющие первой экспоненты компенсируются известными алгоритмами [6,7].
Впрочем точное значение положения ЦСО по дальности неизвестно, определяется с
ошибками, что приводит к возникновению нескомпенсированного остаточного члена
25 м его продольное смещение составит около 1 мм. Другие
составляющие первой экспоненты компенсируются известными алгоритмами [6,7].
Впрочем точное значение положения ЦСО по дальности неизвестно, определяется с
ошибками, что приводит к возникновению нескомпенсированного остаточного члена ![]() одинакового для всех
РЦ и влияющего только на смещение совокупности импульсных откликов в ИХ по оси
времени.
одинакового для всех
РЦ и влияющего только на смещение совокупности импульсных откликов в ИХ по оси
времени.
Получение
аналитической модели, показывающей распределение отражательных свойств ВО в его
ИХ по радиальной координате, требует перехода от частотного описания принятой КЧХ
![]() к временному.
Указанный переход от полученной КЧХ, представленной вектором
к временному.
Указанный переход от полученной КЧХ, представленной вектором ![]() , к временному представлению, как указывалось выше, удобно
производить с помощью обратного БПФ. Эта операция связывает комплексную частотную
, к временному представлению, как указывалось выше, удобно
производить с помощью обратного БПФ. Эта операция связывает комплексную частотную
![]() и импульсную
и импульсную ![]() характеристики
объекта. Под ИХ объекта, следуя этим рассуждениям, нужно понимать совокупность
временных откликов системы обработки, каждый из которых является следствием синхронного
воздействия разночастотных сигналов на соответствующий локальный РЦ поверхности
объекта.
характеристики
объекта. Под ИХ объекта, следуя этим рассуждениям, нужно понимать совокупность
временных откликов системы обработки, каждый из которых является следствием синхронного
воздействия разночастотных сигналов на соответствующий локальный РЦ поверхности
объекта.
В реальных условиях при
обработке информации о ЛА используются дискретные отсчеты отраженных сигналов и
дискретное преобразование Фурье. Обратное дискретное БПФ должно жестко
связывать изменение уровня принятого СПЧ с временем запаздывания в ИХ объекта.
Для проведения аналитических преобразований принятых дискретных отраженных
сигналов будем использовать известную запись для обратного дискретного преобразования
Фурье (ДПФ) в виде
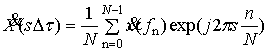 , (6)
, (6)
где ![]() – комплексный
отраженный от ЛА сигнал на
– комплексный
отраженный от ЛА сигнал на ![]() -й частоте, представляющий собой суперпозицию отражений от
локальных РЦ; s - номер отсчета в ИХ объекта; Dt - размер
элемента разрешения по времени.
-й частоте, представляющий собой суперпозицию отражений от
локальных РЦ; s - номер отсчета в ИХ объекта; Dt - размер
элемента разрешения по времени.
Для удобства вычислений преобразуем аргумент экспоненты
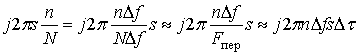 , (7)
, (7)
где Fпер –
общий диапазон перестройки частоты в пачке СПЧ.
Тогда в соответствии с (3) и (5) исходное выражение
для ДПФ, используемого в интересах получения ИХ, будет иметь вид
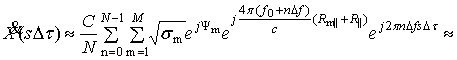
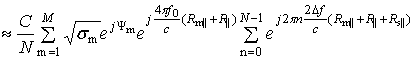 ,
(8)
,
(8)
где ![]() – расстояние от ЦСО
до элемента дальности, соответствующего s-му временному отсчету в формируемой ИХ.
– расстояние от ЦСО
до элемента дальности, соответствующего s-му временному отсчету в формируемой ИХ.
Воспользовавшись заменой ![]() , получим
, получим
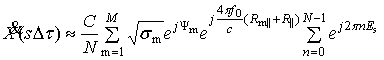 . (9)
. (9)
Наличие под знаком второй суммы членов геометрической
прогрессии позволяет выразить результат суммирования в виде
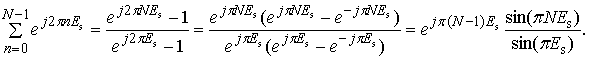 (10)
(10)
Разрешая полученную неопределенность типа
sin(Nx)/sin(x) по правилу Лопиталя, получаем амплитудный выигрыш в N раз, что подтверждает возможность
признания сигналов с управляемой известной перестройкой частоты когерентными,
т.е. возможность когерентного накопления СПЧ.
Подставляя значение ![]() в (10), получаем
формулу для ИХ объекта в дискретном виде
в (10), получаем
формулу для ИХ объекта в дискретном виде
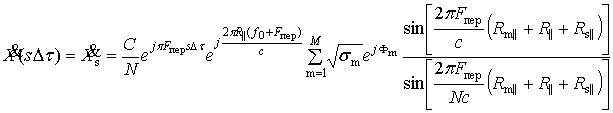 , (11)
, (11)
где ![]() , l0 - длина волны на частоте f0.
, l0 - длина волны на частоте f0.
Можно
заметить, что под знаками обоих синусов присутствует величина, обратная
разрешающей способности по дальности ![]() . Следовательно, ИХ можно выразить через разрешающие
способности, а именно
. Следовательно, ИХ можно выразить через разрешающие
способности, а именно
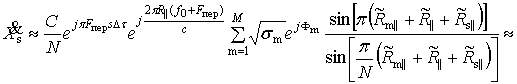 (12)
(12)
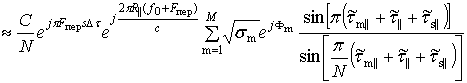 ,
,
где ![]() ,
, ![]() и
и ![]() – относительные дальности от
ЦСО до m-го РЦ, от ЦСО до s-го элемента дальности и остаточная
нескомпенсированная дальность до ЦСО, измеренные в единицах радиальной
разрешающей способности
– относительные дальности от
ЦСО до m-го РЦ, от ЦСО до s-го элемента дальности и остаточная
нескомпенсированная дальность до ЦСО, измеренные в единицах радиальной
разрешающей способности ![]() ;
; ![]() ,
, ![]() и
и ![]() - относительные временные задержки отражений от m-го РЦ, s-го
элемента ИХ и ЦСО (при идеальной компенсации данная задержка и соответствующая
ей дальность во всех элементах выражения для ИХ пропадают), измеренные в
единицах разрешающей способности по времени
- относительные временные задержки отражений от m-го РЦ, s-го
элемента ИХ и ЦСО (при идеальной компенсации данная задержка и соответствующая
ей дальность во всех элементах выражения для ИХ пропадают), измеренные в
единицах разрешающей способности по времени ![]() .
.
Выражение (12) является аналитической моделью ИХ в
комплексной форме. Именно такой ИХ формируется на выходе преобразователя после
перехода от КЧХ к временному описанию. Однако при анализе и использовании в
алгоритмах принятия решений принято оперировать с векторами действительных
чисел или огибающими. Для перехода к такому варианту ИХ целесообразно воспользоваться
операцией получения модуля. Поэтому абсолютная ИХ имеет следующую аналитическую
модель
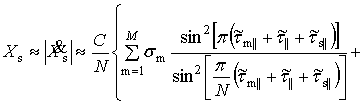
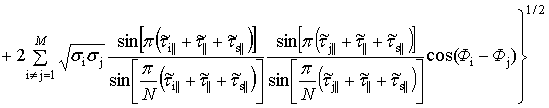 . (13)
. (13)
Аналитическая модель (13) показывает, что ИХ
представляет собой совокупность импульсных откликов типа ![]() . Число таких откликов определяется числом РЦ, разнесенных в
радиальном направлении, а положение на оси времени – индивидуальными задержками
t отражений от соответствующих
РЦ на поверхности ЛА. Интерферирующие члены, выраженные вторым слагаемым в
фигурных скобках, ухудшают разрешение и искажают ИХ ввиду наличия множителя
. Число таких откликов определяется числом РЦ, разнесенных в
радиальном направлении, а положение на оси времени – индивидуальными задержками
t отражений от соответствующих
РЦ на поверхности ЛА. Интерферирующие члены, выраженные вторым слагаемым в
фигурных скобках, ухудшают разрешение и искажают ИХ ввиду наличия множителя ![]() . Моделирование показывает [11-14], что их негативное влияние
проявляется на уровне боковых лепестков, которые в ИХ имеют низкий уровень (практически
отсутствуют) вследствие накопления энергии отдельных импульсных отражений.
Поэтому для ассоциативного описания влиянием разностей фаз можно пренебречь и
ограничиться основным ядром огибающей ИХ в виде
. Моделирование показывает [11-14], что их негативное влияние
проявляется на уровне боковых лепестков, которые в ИХ имеют низкий уровень (практически
отсутствуют) вследствие накопления энергии отдельных импульсных отражений.
Поэтому для ассоциативного описания влиянием разностей фаз можно пренебречь и
ограничиться основным ядром огибающей ИХ в виде
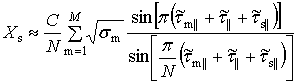 . (14)
. (14)
Главный вывод проведенных исследований заключается в
том, что структура ИХ ЛА действительно должна отражать реальное взаимное
расположение РЦ на поверхности объекта вдоль линии визирования и тем достовернее,
чем меньше длительность пачки СПЧ и меньше скважность (большее число разночастотных
сигналов).
Аналитические модели ИХ (13) и (14) могут использоваться в исследовательских задачах, связанных с моделированием процессов обработки радиолокационной информации в локаторах с режимами идентификации, различения объектов в группах и т.п. При этом необходимо учитывать, что наличие нескомпенсированного остатка дальности до ЦСО может приводить к перераспределению амплитуд импульсных откликов от РЦ между смежными элементами ИХ. Если импульсный отклик от РЦ попадает точно на отсчет ИХ, то амплитуда этого отклика будет максимально близка к истинной отражательной способности соответствующего РЦ. Если же пик отклика попадает между двумя отсчетами в ИХ, то его амплитуда распределяется между двумя этими соседними отсчетами, и видимый пик отклика в огибающей ИХ становится по амплитуде меньше. Этот факт приводит к непредсказуемому изменению амплитуд импульсных откликов и несовпадению последовательно формируемых ИХ даже при незаметном для визуального восприятия изменении ракурса объекта. Поэтому при малейшем повороте ЛА и изменении взаимного удаления РЦ ИХ может эволюционировать, что существенно усложняет анализ результатов.
Предлагаемый способ формирования ИХ не только прост в
реализации, но и достаточно эффективен, так как он реагирует на любые изменения
во взаимном положении РЦ на поверхности планера ЛА. Процесс формирования ИХ
позволяет получать разрешающую способность по времени порядка десятков-сотен
микросекунд, что в пересчете на продольную координату составляет от долей до
единиц метров. Описанный способ получения ИХ ЛА может быть рекомендован
диспетчерским службам аэропортов, контролирующим безопасность взлета и посадки
воздушных судов, а также другим службам, решающим родственные задачи.
Аналитические исследования выполнены в соответствии с
тематикой гранта Российского фонда фундаментальных исследований № 14-07-00193.
Литература
1. Стайнберг Б.Д.
Формирование радиолокационного изображения самолета в диапазоне СВЧ // ТИИЭР.
1988. №12. Т. 76. С.26-46.
2.
Shirman Y.D. Computer simulation of aerial target radar scattering recognition,
detection, and tracking. Norwood. Boston-London. Artech House,
2002. 296 p.
3. Справочник по радиолокации / Под ред. М. И.
Сколника. Пер. с англ. М., Сов. радио, 1967. Т. 1. Основы радиолокации. 456 с.
4. Радиоэлектронные системы. Справочник.
Основы построения и теория / Под ред. Я. Д. Ширмана. М., Радиотехника, 2007. 510 с.
5. Кононов А.Ф. Применение
томографических методов для получения радиолокационных изображений объектов с
помощью сверхширокополосных сигналов // Зарубежная радиоэлектроника, 1991. № 1.
С. 35-49.
6. Митрофанов Д.Г. Метод построения радиолокационных
изображений аэродинамических летательных аппаратов // Полет, 2006. № 11. С 52-60.
7. Майоров Д.А., Савостьянов В.Ю., Митрофанов Д.Г.
Измерение радиальной скорости воздушных объектов в режиме перестройки частоты
// Измерительная техника, 2008. № 2. С 43-47.
8. Патент РФ № 2326402. Способ измерения радиальной
скорости воздушной цели в режиме перестройки частоты от импульса к импульсу.
Савостьянов В.Ю., Майоров Д.А., Прохоркин А.Г., Митрофанов Д.Г. Опубл.
10.06.2008.
9. Митрофанов Д.Г. Формирование двумерного
радиолокационного изображения цели с траекторными нестабильностями полета //
Радиотехника и электроника. РАН. 2002. Том 47. № 7. С. 852-859.
10.
Митрофанов Д.Г. Комплексный адаптивный
метод построения радиолокационных
изображений в системах управления двойного назначения // Теория и
системы управления. Известия РАН. 2006. № 1-2. С. 101-118.
11. Митрофанов Д.Г. Цифровые алгоритмы обработки отраженных сигналов с максимизацией степени когерентности. Труды РНТО РЭС имени А.С.Попова. Серия: Научная сессия, посвященная Дню Радио. Выпуск LXV. М., 2010. С. 130-132.
12. Митрофанов Д.Г. Перспективы развития радиолокационной техники при использовании сигналов с перестройкой частоты. Труды 13-й Всероссийской научно-практической конференции «Актуальные проблемы защиты и безопасности». Том 1. СПб.: НПО специальных материалов, 2010. С. 250-257.
13. Митрофанов Д.Г. Математическое и физическое моделирование дальностных портретов воздушных целей в интересах получения оценок классификации. Приложение к журналу «Известия Российской академии ракетных и артиллерийских наук». Труды 12-й Всероссийской научно-практической конференции «Актуальные проблемы защиты и безопасности». Том 2. СПб.: НПО специальных материалов, 2009. С. 327-342.
14. Митрофанов Д.Г., Майоров Д.А., Заикин Д.Р. Математическая модель частотной характеристики многоточечной цели для условий зондирования сигналами с перестройкой несущей частоты // Электромагнитные волны и электронные системы, 2008. № 11. С. 4-9.