О СИЛЬНОЙ СУММИРУЕМОСТИ РЯДОВ ФУРЬЕ-УОЛША В ПРОСТРАНСТВЕ БЕСОВА.

Бокаев Нуржан Адилханович, г. Астана, ЕНУ;

Игенберлина Алуа Еркиновна, г. Караганда, КарГТУ.

Ряды Фурье-Уолша даже непрерывных функций могут расходиться в отдельных точках, а среди интегрируемых функций существуют такие, что ряды Фурье-Уолша их расходятся всюду на . В связи с этим возникает необходимость рассматривать различные методы суммирования, которые позволили бы восстановить функцию по её ряду Фурье-Уолша. В этой статье исследовано пространство Бесова на двоичной группе в терминах сильной суммируемости. Приведём необходимые сведения о преобразовании Фурье-Уолша.

Пусть задана система функций Уолша в нумерации Пэли. Для

числа и натурального n положим

где означает целую часть числа , по определению равны 0 или 1. Для справедливо разложение

,

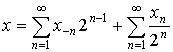при этом

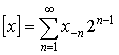и .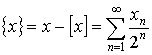

Так как для то для определено целое неотрицательное число

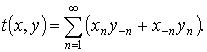
Функция Файна или обобщенная функция Уолша определяется на равенством:

,

следовательно для .

Функция Файна удовлетворяет следующим свойствам:

.

Введем на операцию покоординатного сложения по модулю 2

следующим образом. Пусть для определено разложение, аналогичное (2.2.1). Тогда положим где

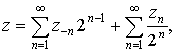
причем , .

Для функции функция Файна порождает преобразование Фурье-Уолша:

.

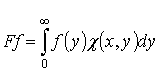Кроме того, имеет место равенство:

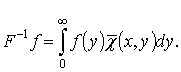
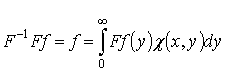
для почти всех , при и .

При р=1 это равенство следует понимать поточечно. При функция понимается как предел по норме при функций

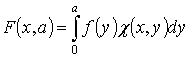, где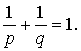

Если , то коэффициенты Фурье-Уолша задаются следующим

образом:

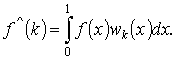
Отметим, что преобразование Фурье-Уолша обладает всеми основными свойствами тригонометрического преобразования Фурье.

В частности при , для двоичной свертки

имеет место равенство:

.

Далее, пусть - действительнозначная, ограниченная функция, определенная на , и имеющая компактный носитель.

Введем средние для

.

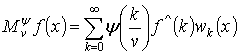- полином Уолша. При различных конкретизациях функции можно получить средние Фейера-Уолша, средние Валле-Пуссена и средние Рисса по системе Уолша.

Рассмотрим сильную аппроксимацию функции этими средними при Возникает вопрос, при каких условиях на и функцию будет выполняться условие:

.

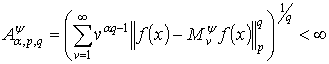где

И обратно, какими свойствами будет обладать функция , если выполняется условие это условие.

Определение 1. Рассмотрим множество Ф систем таких, что

supp, supp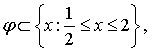

следовательно, supp;

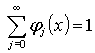, для любого

Определение 2. Пусть ,

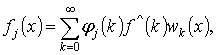
Пространство Бесова определим следующим образом:

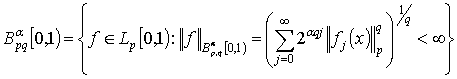, при .

При

.

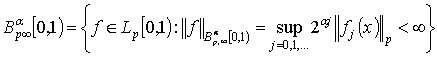Необходимы следующие вспомогательные утверждения:

Пусть

есть максимальная функция Харди-Литлвуда, где супремум берется по всем отрезкам Q с центром в точке .

Максимальное неравенство Феффермана-Стейна

Пусть . Тогда существует положительная постоянная С такая, что для всех

:

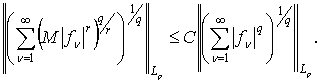
Отсюда, при и получим:

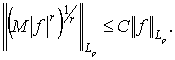
Известно, что при для функции

имеет место следующее

Неравенство Никольского

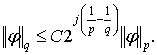
Лемма 1. Пусть - полином по системе Уолша и такая, что тогда

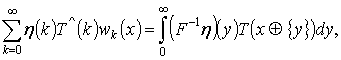
для всех .

Лемма 2. Пусть 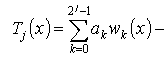полином Уолша, функция:

Тогда, для любого

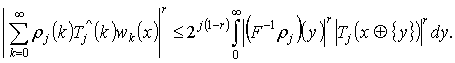
Лемма 3. Пусть и такая, что ,

и

.

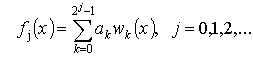Тогда, существует постоянная С, не зависящая от такая, что для

каждого

.

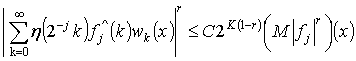Ответы на поставленные вопросы дают следующие утверждения:

Теорема 1. Пусть , непрерывная функция на , имеющая компактный носитель; а и пусть такое, что для любого

.

Тогда при выполняется условие

.

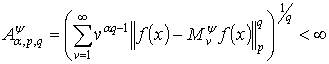и существует постоянная С` такая, что:

.

Теорема 2. Пусть, ограниченная функция на , с компактным носителем и пусть существует натуральное число d, удовлетворяющее условию:

для .

Пусть и выполняется условие

.

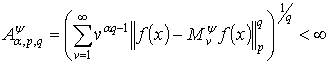Тогда и существует положительная постоянная С``, не зависящая от такая, что имеет место оценка:

.
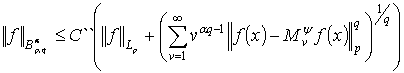