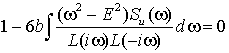Технические
науки/2. Механика
Бакиров Ж.Б., Михайлов В.Ф.
Карагандинский
государственный технический университет, Казахстан
Исследование устойчивости случайных
нелинейных колебаний
Нелинейные задачи динамики весьма актуальны для
инженерной практики в связи с повышением уровня нагруженности механизмов и
машин, увеличением их скоростей. Среди этих задач недостаточно изученными остаются
нелинейные задачи статистической динамики. В настоящее время получены
стационарные решения случайных колебаний упругих систем с учетом геометрической
нелинейности [1; 2]. Эти решения могут приводить к неоднозначным зависимостям для
статистических характеристик, особенно при узкополосных случайных воздействиях.
Среди неоднозначных решений необходимо выделить ветви, соответствующие
устойчивым режимам. Эта задача решается на основе уравнений в вариациях, составленных
по отношению к исходным нелинейным уравнениям.
Колебания тонкой
упругой цилиндрической панели под действием случайных сил при одночленном
приближении описываются нелинейным уравнением вида
где ![]() — смещение в
центре панели;
— смещение в
центре панели; ![]() ,
, ![]() — частота и
коэффициент затухания колебаний; параметры нелинейности
— частота и
коэффициент затухания колебаний; параметры нелинейности ![]() ,
, ![]() зависят от
размеров панели;
зависят от
размеров панели; ![]() — обобщенная случайная
сила. При
— обобщенная случайная
сила. При ![]() получаем
известное уравнение Дуффинга, описывающее нелинейные колебания стержней и
пластин, а также движение ряда других механических систем.
получаем
известное уравнение Дуффинга, описывающее нелинейные колебания стержней и
пластин, а также движение ряда других механических систем.
Будем считать, что
стационарное решение уравнения известно, то есть известно распределение случайной функции ![]() и все ее
статистические характеристики. Поставим вопрос об устойчивости стационарного режима.
Представим возмущенное движение системы как сумму двух случайных функций:
и все ее
статистические характеристики. Поставим вопрос об устойчивости стационарного режима.
Представим возмущенное движение системы как сумму двух случайных функций:
![]() ,
,
где ![]() имеет смысл
случайной вариации, то есть отклонения от стационарного решения
имеет смысл
случайной вариации, то есть отклонения от стационарного решения ![]() , которую рассматриваем как нестационарный процесс.
Подставляя это выражение в уравнение получаем нелинейное стохастическое уравнение в вариациях. Линеаризуя полученное
уравнение, имеем
, которую рассматриваем как нестационарный процесс.
Подставляя это выражение в уравнение получаем нелинейное стохастическое уравнение в вариациях. Линеаризуя полученное
уравнение, имеем
Итак, задача об устойчивости
стационарного режима сводится к исследованию эволюции во времени статистических
характеристик отклонения ![]() . При этом исходный режим играет роль параметрического
воздействия.
. При этом исходный режим играет роль параметрического
воздействия.
В соответствии со
спектральным методом введем интегральное представление процессов:
![]() ;
;
где ![]() и
и ![]() — неизвестные
детерминированные функции;
— неизвестные
детерминированные функции; ![]() ,
, ![]() — случайные
спектры.
— случайные
спектры.
Допустим, что
для исходного уравнения получено приближенное решение, основанное на гипотезе гауссовости
процесса ![]() . Тогда относительно функций
. Тогда относительно функций ![]() ,
, ![]() по изложенной
выше методике нетрудно вывести систему дифференциальных уравнений в среднем и
среднеквадратичном. Подставляя в , находим
по изложенной
выше методике нетрудно вывести систему дифференциальных уравнений в среднем и
среднеквадратичном. Подставляя в , находим
Осредняя это уравнение,
получим
где ![]() .
.
Перейдем в в пространство Фурье, умножим полученное уравнение на комплексно-сопряженный
спектр ![]() и произведем
осреднение, предполагая спектр
и произведем
осреднение, предполагая спектр ![]() квазигауссовским.
В результате дальнейшего интегрирования по частоте
квазигауссовским.
В результате дальнейшего интегрирования по частоте ![]() , получим уравнение движения в среднеквадратичном,
дающее связь между спектрами
, получим уравнение движения в среднеквадратичном,
дающее связь между спектрами
При выводе этого уравнения
моментная функция четвертого порядка с учетом свойства гауссовости выражена
через моменты второго порядка по известным формулам, как это сделано ранее для
нелинейного члена ![]() :
:
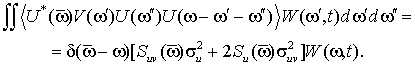
Соотношения между спектрами ![]() и
и ![]() , а также между математическими ожиданиями
, а также между математическими ожиданиями ![]() и
и ![]() можно получить
из стационарного решения . Это решение находится из и , если положить в них при
можно получить
из стационарного решения . Это решение находится из и , если положить в них при ![]()
![]() , а
, а ![]() . Тогда имеем
. Тогда имеем
![]() ;
; ![]() ,
,
где ![]() .
.
Если отсюда исключить ![]() , то получим
, то получим
Для решения уравнений и воспользуемся операторным методом. Из уравнения следует
![]() ,
,
где ![]() ;
; ![]() ;
;
![]() — изображения соответствующих
функций. Из уравнения , учитывая последнее равенство, получаем характеристическое уравнение
устойчивости
— изображения соответствующих
функций. Из уравнения , учитывая последнее равенство, получаем характеристическое уравнение
устойчивости
![]() .
.
С учетом равенства можно записать
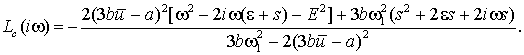
После математических
преобразований характеристическое уравнение можно привести к следующему виду
где
![]() ;
; ![]() .
.
Вероятностные характеристики
процесса ![]() (
(![]() ,
, ![]() ,
, ![]() ) определяются из стационарного решения исходной
нелинейной задачи. После вычисления интеграла (9) исследование устойчивости
сводится к процедуре Рауса—Гурвица для полинома, вытекающего из уравнения .
) определяются из стационарного решения исходной
нелинейной задачи. После вычисления интеграла (9) исследование устойчивости
сводится к процедуре Рауса—Гурвица для полинома, вытекающего из уравнения .
В качестве примера
рассмотрим уравнение Дуффинга (![]() =0) при центрированном случайном воздействии. В этом
случае
=0) при центрированном случайном воздействии. В этом
случае ![]() =0 и из уравнения следует
=0 и из уравнения следует ![]() , а из уравнения
, а из уравнения
![]() ,
,
где ![]() совпадает с при
совпадает с при ![]() . Проинтегрируем последнее уравнение по частоте и получим
характеристическое уравнение относительно параметра Лапласа
. Проинтегрируем последнее уравнение по частоте и получим
характеристическое уравнение относительно параметра Лапласа
При идеально-узкополосном
воздействии с несущей частотой ![]() из решения нелинейной
задачи имеем [3]
из решения нелинейной
задачи имеем [3]
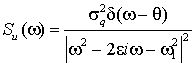 ;
; 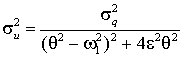 .
.
Введем безразмерные
параметры
![]() ,
, ![]() ,
, ![]() ,
, ![]()
и уравнение для определения
дисперсии запишем в виде
![]() .
.
Подставляя ![]() в , получим
в , получим
![]() .
.
Введем обозначения
![]() ,
, ![]() ,
, ![]()
и перепишем
характеристическое уравнение в безразмерном виде. Тогда относительно параметра ![]() получим полином
четвертой степени с коэффициентами:
получим полином
четвертой степени с коэффициентами:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Далее исследование
устойчивости по процедуре Рауса—Гурвица сводится к выполнению следующих
неравенств
![]() ;
;
Второе неравенство можно
переписать так:
![]() .
.
Это неравенство выполняется
всегда, следовательно, колебания будут устойчивыми, если выполняется первое
неравенство .
Литература:
1. Макаров
Б.П. Нелинейные задачи стохастической динамики машин и приборов. М.: Машиностроение,
1983.—264с.
2. Болотин
В.В. Случайные колебания упругих систем. М.: Наука, 1979.—336с.
3. Бакиров
Ж.Б., Михайлов В.Ф. Применение спектрального метода к анализу нелинейных случайных
колебаний // Доклады АН ВШ. Естественные науки, №1. Новосибирск, 2008. С. 6-15.
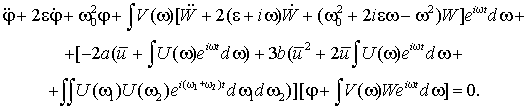
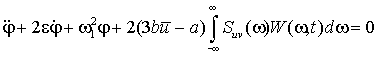
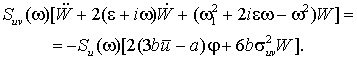
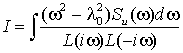 ;
;